Enoncé Mathématiques série D 2011
Résumé de section
-
Nous mettons à votre disposition des sujets de Mathématiques
proposés au baccalauréat série D à Madagascar
Baccalauréat de l'enseignement général
Madagascar
Session 2011
MATHEMATIQUES – Série : D
N.B : - Les DEUX exercices et le Problème sont obligatoires.
- Machine à calculer scientifique NON programmable autorisée.
EXERCICE 1 (5 points) corrigé
Soit l’équation (E) : 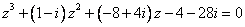
1°) Montrer que (E) admet une solution imaginaire pure 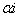 où
où 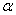 est un nombre réel que l’on
est un nombre réel que l’on
déterminera. (0,5pt)
2°) a- Montrer que (E) peut s’écrire sous la forme :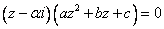 où a, b, c sont
où a, b, c sont
des nombres complexes à déterminer. (0,75 pt)
b- Résoudre dans C l’équation (E) (0,75pt)
3°) Dans le plan complexe (P) muni d’un repère orthonormé direct 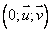 , d’unité 1 cm,
, d’unité 1 cm,
on donne les points A,B, et C d’affixes respectives 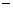 2i ; 3 + i et
2i ; 3 + i et 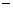 4+ 2i.
4+ 2i.
a- Placer les points A, B, et C dans le plan (P). (0,25pt)
b- On pose 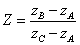
Ecrire 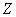 sous forme trigonométrique. (0,5 pt)
sous forme trigonométrique. (0,5 pt)
c- En déduire la nature du triangle ABC. (0,5pt)
d- Trouver l’affixe du point D pour que le quadrilatère ABCD soit un parallélogramme (0,5pt)
4°) Soit S la transformation d’expression complexe 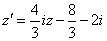
a- Quelle est la nature de S et donner ses éléments caractéristiques. (0,25pt + 0,5pt)
b- Construire l’image 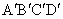 de ABCD par
de ABCD par 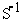 . (0,5pt)
. (0,5pt)
EXERCICE 2 (5 points) corrigé
I ) Une urne contient 8 boules indiscernables au toucher dont :
. 3 rouges numérotées : 2 ; 2 ; 5
. 5 blanches numérotées : 1 ; 2 ; 3 ; 4 ; 5.
1) Le jeu consiste à tirer au hasard et simultanément deux boules de l’urne.
Calculer la probabilité de chacun des événements suivants :
A : « obtenir deux boules de couleurs différentes » (0,25pt)
B : « obtenir deux boules de numéros pairs » (0,5 pt)
C : « obtenir deux boules dont le produit des numéros est égal à 4 » (0,5 pt)
2) On tire au hasard et successivement avec remise 3 boules de l’urne.
Soit X la variable aléatoire définie par le nombre de boules portant le numéro 5 obtenu.
a) Déterminer l’univers image de X (0,5pt)
b) Donner la loi de probabilité de X (0,75pt)
NB : On donnera les résultats sous forme de fraction irréductible.
II) On donne sur le tableau ci-dessous le nombre d’élèves d’un lycée ayant réussi le Baccalauréat durant
4 années successives :
|
Année |
2007 |
2008 |
2009 |
2010 |
|
Rang de l’année(xi) |
1 |
2 |
3 |
4 |
|
Nombre d’élèves en centaine (yi) |
3 |
5 |
6 |
9 |
1) Représenter le nuage des points Mi (xi, yi) 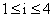 associé à cette série statistique. (0,75pt)
associé à cette série statistique. (0,75pt)
Echelle : sur l’axe des abscisses, prendre 1cm pour représenter une unité.
sur l’axe des ordonnées, placer 2 à l’origine des axes puis prendre 1cm pour
représenter 100 élèves.
2) Déterminer le point moyen G. (0,5pt)
3) Calculer le coefficient de corrélation r et interpréter. (0,5pt)
4) Ecrire l’équation de la droite de régression de y en x. (0,5pt)
5) Combien de réussites peut-on espérer en 2014 ? (0,25pt)
NB : Les résultats seront donnés à 10-2 près.
PROBLEME (10 points) corrigé
On considère la fonction numérique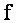 définie sur IR par :
définie sur IR par :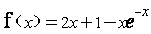
On note (C) sa courbe représentative dans un plan muni d’un repère orthonormé 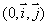 d’unité 2cm.
d’unité 2cm.
1) Soit g la fonction numérique définie sur IR par : 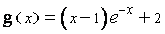
a- Etudier les variations de g et dresser son tableau de variation. (0,5pt+0,5pt)
b- Démontrer que l’équation 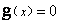 admet une solution unique notée
admet une solution unique notée 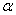 dans IR
dans IR
et que 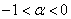 . (0,5pt)
. (0,5pt)
c- En déduire le signe de 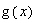 suivant les valeurs de
suivant les valeurs de  . (0,5pt)
. (0,5pt)
2) a- Calculer 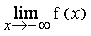 et
et 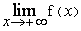 . (0,25 pt x2)
. (0,25 pt x2)
b- Calculer la dérivée 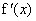 et montrer que :
et montrer que :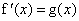 pour tout
pour tout  élément de IR. (0,5pt)
élément de IR. (0,5pt)
c- Montrer que 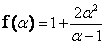 . (0,5pt)
. (0,5pt)
d- Dresser le tableau de variation de 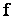 . (0,5pt)
. (0,5pt)
3) a- Calculer 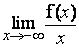 et interpréter graphiquement ce résultat. (0,25 pt x2)
et interpréter graphiquement ce résultat. (0,25 pt x2)
b- Démontrer que la droite (D) : 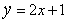 est asymptote à (C) au voisinage de
est asymptote à (C) au voisinage de 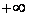 (0,5pt)
(0,5pt)
c- Etudier la position de (C) par rapport à (D). (0,5pt)
4) a- Ecrire une équation de la tangente (T) à (C) au point d’abscisse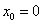 . (0,5pt)
. (0,5pt)
b- Montrer qu’il existe un point A de (C) où (C) admet une tangente (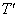 ) parallèle à (D). (0,25pt)
) parallèle à (D). (0,25pt)
Trouver les coordonnées du point A. (0,25pt)
5) Tracer (D), (T), (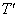 ) et (C) dans le même repère. Pour la construction, on prendra
) et (C) dans le même repère. Pour la construction, on prendra
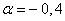 et
et 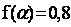 . (0,25ptx3+1,25pt)
. (0,25ptx3+1,25pt)
6) a- A l’aide d’une intégration par partie ; calculer 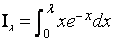 (0,5pt)
(0,5pt)
b- Déterminer, en cm2 , l’aire A 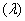 du domaine plan délimité par (C), (D) et les droites
du domaine plan délimité par (C), (D) et les droites
d’équations 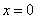 et
et 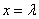 , (
, (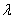 > 0 ) (0,5pt)
> 0 ) (0,5pt)
c- Calculer 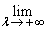
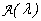 . (0,5pt)
. (0,5pt)

