Enoncé Mathématiques série A 2003
Baccalauréat de l'enseignement général
Madagascar
Session 2003
mathematiques – Série : A
N.B. : Le candidat doit traiter les DEUX Exercices et le Problème.
- - - - - - - - - - - - - - - - - - -
Exercice 1 (5 points) corrigé
Dans une classe de douze élèves, la répartition suivant l’âge et le sexe est donnée par le tableau suivant :
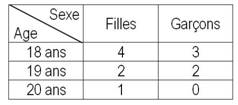
On choisit au hasard et simultanément trois élèves de la classe.
1. Déterminer le nombre de choix possibles. (0,5 pt)
2. Calculer la probabilité de chacun des événements suivants :
A. « les élèves choisis sont des filles ». (0,75 pt)
B. « les élèves choisis ont plus de 18 ans ». (1 pt)
C. « les trois élèves choisis ne sont pas de même sexe ». (1,25 pt)
D. « au moins un élève choisi a exactement 19 ans ». (1,5 pt)
Exercice 2 (5 points) corrigé
On considère la suite (un) définie par : u1 = 5 et un + 1 = 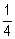 un +
un + 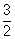 .
.
On pose vn = un – 2.
1. Calculer u2 , u3 et v1 . (0,75 pt)
2. Montrer que (vn) est une suite géométrique de raison 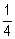 . (1 pt)
. (1 pt)
3. Exprimer vn puis un en fonction de n. (0,5 + 0,25 pt)
4. On pose wn = ln vn où ln est le logarithme népérien.
a) Montrer que (wn) est une suite arithmétique dont on déterminera la raison et le premier terme. (1,5 pt)
b) Exprimer Sn = w1 + w2 +… + wn en fonction de n. (1 pt)
Problème (10 points) corrigé
Soit f la fonction définie par f(x) = 1 – 2x + ex. On note (C ) la courbe représentative de f dans un repère orthonormé (O,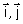 ) d’unité 1 cm.
) d’unité 1 cm.
1. a) Déterminer l’ensemble de définition de f. (0,75 ; 0,50)
b) Calculer 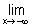 f(x). (0,75 ; 0,50)
f(x). (0,75 ; 0,50)
c) En remarquant que pour tout x > 0, f(x) = x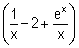 , calculer
, calculer 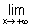 f(x). (On donne
f(x). (On donne 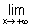
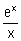 = +
= + ). (0,75 ; 0,50)
2. a) Calculer f ’(x). (1,00 ; 0,75)
b) En déduire le tableau de variation de f. (1,25 ; 1,00)
3. a) Déterminer les coordonnées du point A, intersection de la courbe (C ) avec l’axe des ordonnées. (1,00 ; 0,75)
b) Ecrire l’équation de la tangente (T) à (C ) au point A. (1,00 ; 1,00)
4. a) Calculer 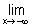 [f(x) – (– 2x + 1)]. Que peut-on en conclure ? (1,00 ; 1,00)
[f(x) – (– 2x + 1)]. Que peut-on en conclure ? (1,00 ; 1,00)
b) Etudier la branche infinie de (C ) lorsque x tend vers + . On admet que
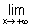
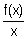 = +
= + . (1,00 ; 0,75)
5. Tracer (C ). (1,50 ; 1,25)
Pour A2 seulement
6. a) Donner une primitive de f sur IR. (0,00 ; 1,00)
b) En déduire l’aire géométrique en cm2, du domaine plan limité par la courbe (C ), l’axe des abscisses et les droites d’équations respectives x = 0 et x = ln 2. (0,00 ; 1,00)
On donne : ln 2 ≈ 0,7.