Série A - Mathématiques

Baccalauréat de l'enseignement général

Madagascar

Session 2008

 

mathematiques    –  Série : A

 

NB :     - Les deux exercices et le problème sont obligatoires.

                                                           - Machine à calculer autorisée.

 

Exercice  1    (5 points)                                                                                                        corrigé

 

1)       (U_n)_nIN est la suite arithmétique définie par : U₂₃ = 71 et  U₇₅ = 227.

a)      Calculer la somme S définie par  S = U₂₃ + U₂₄ +  . . . + U₇₅.                                                 (1)

b)     Calculer la raison de la suite (U_n)_nIN.                                                                                   (1)

c)      Exprimer U_n en fonction de n.                                                                                              (1)

2)       (V_n)_nIN est la suite numérique définie, pour tout entier naturel n, par V_n = 2.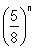                          

a)      Exprimer V_n+1 en fonction de V_n. En déduire la nature et la raison de la suite (V_n)_nIN.                                                                                                                                     (0,5+0,5)

b)      Calculer la limite de la suite (V_n)_nIN.                                                                                     (1)

 

 

Exercice  2    (5 points)                                                                                   corrigé

 

Le tableau suivant donne le nombre de téléphones mobiles vendus, pendant huit années successives, par un distributeur agréé :

 

Rang de l’année (xi)	1	2	3	4	5	6	7	8
Nombre de téléphones vendus (yi)	26 000	28 000	50 000	65 000	81 000	83 000	120 000	125 000

1)   Représenter le nuage de points {M_i }_{1 ≤ i ≤ 8}  associé à cette série statistique.                                  (1)

    (Echelle : Axe des abscisses : 1 cm représente une année

Axe des ordonnées : 1 cm représente 10 000 téléphones vendus)

2)   On partage le nuage de points en deux parties d’effectifs égaux {M₁, M₂, M₃, M₄} et {M₅, M₆, M₇, M₈}.

a)      Calculer les coordonnées de G₁ et G₂, points moyens respectifs des nuages partiels ainsi obtenus.                                                                                                                                           (1 + 1)

b)     Représenter la droite (G₁G₂). Ecrire une équation cartésienne de cette droite.                                                                                                                                               (0,5+0,5)

3)   En supposant que l’évolution du nombre de téléphones vendus par ce distributeur gardera la même tendance, déterminer ce nombre pour la dixième année, à l’aide de la droite d’ajustement (G₁G₂) de cette série.                                                                                                                                          (1)

 

 

 

 

PROBLEME            (10 points)                                                                        corrigé

 

f est la fonction numérique définie sur  ]0 ; +∞[  par  f(x) = 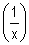(lnx).

On note (C ) la courbe représentative de f dans un plan (P ) muni d’un repère orthonormé (O, 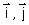) d’unité graphique 2 cm .

     A1             A2

 

1)       a)      Calculer 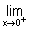f(x). Interpréter graphiquement ce résultat.                                               (1+ 0,5)  (0,5 x 2)

b)     On rappelle que 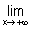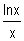= 0. En déduire 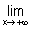f(x).                                                     (1)            ( 0,5)

2)       a)      Montrer que pour tout réel x de ]0 ; +∞[ : f’(x) =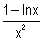où f’est la fonction dérivée de f.                                                                                                                                 (1,5)         (1)                           

b)     Résoudre, dans] 0 ; +∞ [, l’équation (1 – lnx) = 0.                                                        (1)          (0,5)

c)      Dresser ensuite le tableau de variation de f sur ]0 ; +∞ [.                                             (1,5)       (1,5)

3)       a)      Donner une équation de la tangente (T) à  (C ) au point A d’abscisse x₀ = 1.                (1)          (1)

b)     Tracer, uniquement sur l’intervalle ] 0 ; e], la courbe (C ), son asymptote verticale et ses deux tangentes aux points A  et B (e ;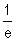) ; dans le même repère (O, 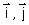).                         (0,5x3+1)                                                                                                                                 (0,5x3+1)

(On prendra e = 2,7 et 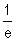= 0,4 ; uniquement pour construire).                                     

 

Pour A2 seulement

                                                                                                                                        

4)   F est la fonction numérique définie par F(x) = 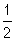 (lnx)² + 3 pour tout réel x de ]0 ; +∞ [.                      

a)      Montrer que F est une primitive de f sur ]0 ; +∞ [.                                                                        (1)

b)     En déduire l’aire, en cm², du domaine plan délimité par la courbe (C ), l’axe des abscisses et les droites d’équations x = 1 et x = e.                                                                                         (1)