Enoncé Mathématiques série A 2011
Résumé de section
-
Nous mettons à votre disposition des sujets de Mathématiques
proposés au baccalauréat série A à Madagascar
Baccalauréat de l'enseignement général
Madagascar
Session 2011
MATHEMATIQUES – Série : A
N.B : - Les DEUX (02) exercices et le Problème sont obligatoires.
- Machine à calculer scientifique NON programmable autorisée.
Exercice 1 (05 points) corrigé
On considère les suites numériques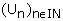 
et 
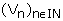définies respectivement par :
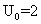
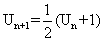et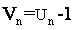 
1°) Calculer U1 ,V0 et V1 (0,25 pt x3)
2°)a) Montrer que 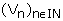est une suite géométrique de raison 
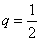(1pt)
b) Exprimer Vn puis Un en fonction de n (0,5pt+0,5pt)
3°) Soit la suite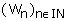 
définie par :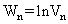 
a) Montrer que (Wn) est une suite arithmétique dont on précisera sa raison et son premier terme. (1pt)
b) Ecrire Wn en fonction de n et calculer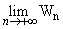 
( 1pt + 0,25pt)
Exercice 2 (05 points) corrigé
Une boîte contient 10 jetons indiscernables au toucher dont 3 jaunes, 2 rouges et 5 blancs.
1°) On tire au hasard et simultanément 3 jetons de la boîte.
a) Déterminer le nombre de cas possibles. (1pt)
b) Calculer la probabilité de chacun des événements suivants :
A : « Obtenir trois jetons de même couleur ». (1pt)
B : « Parmi les trois jetons tirés, deux et deux seulement sont de même couleur ». (1pt)
2°) On tire au hasard et successivement sans remise 3 jetons de la boîte.
Calculer la probabilité de chacun des événements suivants :
C : « Obtenir dans l’ordre un jeton rouge et deux jetons blancs ». (1pt)
D : « Les deux jetons rouges sont tirés ». (1pt)
NB : On donnera les résultats sous forme de fraction irréductible.
Problème ( 10 points) corrigé
A1 A2
Soit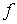 
la fonction numérique définie sur IR par :
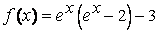
On note ( C ) sa courbe représentative dans un repère orthonormé (0 ;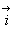
,
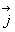) d’unité 1cm.
1°) Vérifier que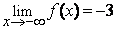 
. Interpréter géométriquement ce résultat. (1+0,5pt) (0,5pt)
2°)a) Calculer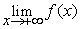 
. (1pt) (0,5pt)
b) Sachant que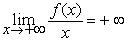 
. Que peut- on dire pour la courbe ( C ) ? (0,75pt) (0,5pt)
3°) Déterminer les coordonnées du point A , intersection de la courbe ( C ) avec l’axe des
abscisses (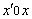
). (0,75pt) (0,75pt)
4°)a) Vérifier que pour tout réel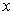 
de IR, 
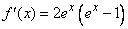où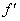 
est la fonction
dérivée de 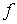. (1pt) (1pt)
b) Etudier le sens de variation de 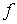et dresser son tableau de variation sur IR (1+0,5pt) (1+0,5pt)
5°) Ecrire une équation de la tangente (T) à ( C ) au point d’abscisse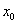 
= ln3. (1pt) (1pt)
6°) Montrer que le point I(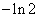 
; 
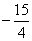) est un point d’inflexion pour la courbe ( C ). (1pt) (0,75pt)
7°) Tracer (T) et ( C ) dans le même repère. (0,5+1pt) 0,5+1pt)
Pour A2 seulement
8°) soit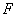 
la fonction définie sur IR par :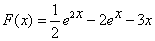 
a) Prouver que 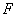est une primitive de 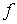sur IR. (0,00pt) (1pt)
b) Calculer, en cm2, l’aire A du domaine plan délimité par la courbe ( C ),
l’axe (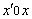) et les droites d’équations respectives : 
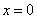et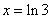 
. (0,00pt) (1pt)
On donne : ln 2 = 0,7 et ln 3 = 1,1