Enoncé Mathématiques série D 2009
Baccalauréat de l'enseignement général
Madagascar
Session 2009
MATHEMATIQUES – Série : D
N.B. : - Les deux Exercices et le Problème sont obligatoires.
- Machine à calculer scientifique non programmable autorisée.
EXERCICE 1 (5 points) corrigé
Le plan complexe (P ) est muni d’un repère orthonormé (O ;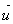 
; 
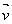) d’unité : 1 cm
1) P est le polynôme de la variable complexe z défini par :
P(z) = z3 – (6+2i)z2 + (10+8i)z – 4 – 8i.
a) Calculer P(2). (0,25pt)
b) Résoudre dans C, l’équation P(z) = 0. (1pt)
2) On donne les points A, B, C et D d’affixes respectives a = 1 + i ; b = 2 ; c = 3 + i et d.
a) Calculer d pour que ABCD soit un carré. (0,75 pt)
b) On considère la similitude plane directe S définie par son expression complexe : z’ = (1 + i) z + 4i
- Donner les éléments caractéristiques de S. (1 pt)
- Déterminer l’expression analytique de S. (1 pt)
3) Construire dans le même repère ABCD et A’B’C’D’ son image par S. (1 pt)
EXERCICE 2 (5 points) corrigé
1) Les faces d’un dé cubique D1 truqué sont numérotées : 1 ; 2 ; 2 ; 3 ; 3 ; 3.
On lance une fois ce dé. Chaque face a la même probabilité d’apparition.
On note Pi la probabilité d’apparition de la face portant le numéro i.
Calculer P1, P2 et P3. (0,25 + 0,25 + 0,25)
2) Les faces d’un deuxième dé cubique normal D2 sont numérotées de 1 à 6.
On lance en même temps les deux dés D1 et D2.
Chaque face a toujours la même probabilité d’apparition.
a) Calculer la probabilité de l’événement :
A : « les deux dés affichent le même numéro » (0,5 pt)
b) On désigne par X la variable aléatoire définie par la somme des numéros affichés par les deux dés.
- Donner la loi de probabilité de X (1 pt)
- Calculer l’espérance mathématique E(X). (1 pt)
3) On lance trois fois de suite et d’une façon indépendante le dé D1.
On note Y la variable aléatoire égale au nombre d’apparitions de la face portant le numéro 2 lors de ces trois lancers.
a) Donner la loi de probabilité de Y. (1 pt)
b) Calculer la variance V(Y). (0,75 pt)
NB : Tous les résultats seront exprimés sous forme de fraction irréductible.
PROBLEME (10 points) corrigé
On considère la fonction numérique f de la variable réelle x définie par :
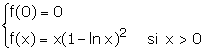
où ln désigne la fonction logarithme népérien.
On appelle (C) sa courbe représentative dans un repère orthonormé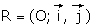 
d’unité : 1cm.
1) Justifier que l’ensemble de définition de f est [0 ;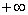 
[. (0,5 pt)
2) a) Prouver que f est continue en x0 = 0. (0,75 pt)
b) Etudier la dérivabilité de f en xo = 0. (0,5 pt)
3) a) Démontrer que pour tout x > 0 ; f’(x) = (lnx - 1)(lnx + 1) où f’ désigne la fonction dérivée première de f. (0,5 pt)
b) Après avoir précisé le sens de variations de f, dresser son tableau de variations. (0,5 + 0,5)
4) Tracer la courbe (C). (2 pts)
5) Soit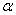 
un réel appartenant à l’intervalle ]0 ; e[.
a) Calculer, à l’aide de deux intégrations par parties l’intégrale
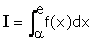(1,5 pts)
b) Soit A (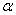) l’aire du domaine plan délimité par l’axe (O , 
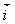), les droites d’équations x = 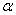et x = e et la courbe (C).
Calculer en cm2 A (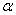) et
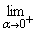A (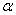). (0,25 + 0,25)
6) Soit g la restriction de f à l’intervalle [e ; [.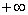
a) Démontrer que g admet une application réciproque notée g-1 dont on précisera l’ensemble de définition. (1 pt)
b) Calculer g(e2) et (g-1)’(e2) (0,25 + 0,5)
7) Tracer dans le même repère que (C) la courbe représentative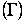 
de g-1 (1 pt)
On donne e ≈ 2,7 ; e-1≈0,36 ; e2≈7,4