Enoncé Mathématiques série A 2000
Baccalauréat de l'enseignement général
Madagascar
Session 2000
mathematiques – Série : A
Exercice 1 (4 points) corrigé
N.B. : – Les questions 1., 2. et 3. sont indépendantes.
– On donnera les résultats sous forme de fraction irréductible.
Une urne contient 8 boules indiscernables au toucher dont 4 blanches et 4 noires.
1. On tire au hasard et simultanément 3 boules de l’urne.
a. Déterminer le nombre de tirages possibles. (0,5 pt)
b. Quelle est la probabilité d’obtenir 3 boules blanches ? (0,5 pt)
c. Quelle est la probabilité d’obtenir 1 boule blanche et 2 boules noires ? (0,5 pt)
2. On effectue 3 tirages successifs d’une boule, en remettant dans l’urne, avant chaque tirage, la boule précédemment tirée.
a. Quel est le nombre de tirages possibles ? (0,5 pt)
b. Quelle est la probabilité de sortir ainsi 3 boules noires ? (0,5 pt)
c. Quelle est la probabilité de sortir ainsi 1 blanche puis 2 noires ? (0,5 pt)
3. On tire toutes les boules une à une sans remise.
a. Quel est le nombre de tirages possibles ? (0,5 pt)
b. Quelle est la probabilité pour que les couleurs de toutes les boules tirées soient alternées ? (0,5 pt)
Exercice 2 (4 points) corrigé
Le tableau suivant montre le chiffre d’affaires, exprimé en millions de francs malagasy, d’une entreprise au cours des six dernières années.
|
Année |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Rang : xi |
1 |
2 |
3 |
4 |
5 |
6 |
|
Chiffre d’affaires : yi |
120 |
132 |
147 |
164 |
181 |
201 |
1. Calculer la moyenne de la série (yi). (0,5 pt)
2. Représenter dans un repère orthogonal le nuage de points Mi ( xi ,yi). (Sur l’axe des abscisses, 2 cm représente une année ; sur l’axe des ordonnées, 1 cm représente 20 millions). (1,5 pt)
3. Soit G1 le point moyen du sous–nuage obtenu par x1 , x2 et x3 ; G2 le point moyen du sous-nuage obtenu par x4 , x5 et x6.
a. Déterminer les coordonnées de G1 et de G2. (0,5 pt)
b. Tracer la droite (G1G2). Que représente cette droite ? (0,5 pt)
c. Donner l’équation de la droite (G1G2). (0,5 pt)
d. En déduire une prévision du chiffre d’affaires de cette entreprise en 2002. (0,5 pt)
Problème (12 points) corrigé
Soit f la fonction définie sur l’intervalle ] – 4 ; 2 [ par : f (x) = ln (x + 4) – ln (2 – x).
On note par (C) la courbe représentative de f dans un repère orthonormé (O ; 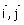 ), d’unité 2 cm.
), d’unité 2 cm.
1. Calculer les limites de f en – 4 et en 2. Interpréter graphiquement ces résultats. (2 pts)
2. a. Montrer que, pour tout x ] – 4 ; 2 [, la fonction dérivée de f est :
f ’ (x) = 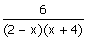 . (1 pt)
. (1 pt)
b. Dresser le tableau de variation de f. (1 pt)
3. a. Déterminer le point d’intersection de (C) avec l’axe des abscisses. (1 pt)
b. Ecrire l’équation de la tangente (T) à (C) au point I( –1 ; 0 ). (1 pt)
c. Montrer que le point I ( –1 ; 0 ) est un centre de symétrie pour (C). (1 pt)
4. Tracer (T) et (C) dans un même repère. (2 pts)
5. Soit F la fonction définie sur l’intervalle ] – 4 ; 2 [ par :
F (x) = ( x + 4 ) ln ( x + 4 ) – ( x – 2 ) ln ( 2 – x ).
a. Calculer la fonction dérivée F ’ de F. (1 pt)
b. En déduire la valeur exacte en cm² de l’aire du domaine plan limité par (C), l’axe des abscisses et les droites d’équations x = – 1 et x = 0. (1 pt)
6. Soit g la fonction définie sur ] – 4 ; 2 [ par :
g (x) = ln 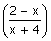 .
.
a. Montrer que, pour tout x ] – 4 ; 2 [ : g (x) = – f (x). (0,5 pt)
b. Tracer dans le même repère que (C) la courbe représentative de g. (0,5 pt)