Enoncé Mathématiques série A 2002
Baccalauréat de l'enseignement général
Madagascar
Session 2002
mathematiques – Série : A
N.B. : Le candidat doit traiter les DEUX exercices et le problème.
-------------------------------------------------------------------------------------------
EXERCICE 1 ( 4 points ) corrigé
On considère la suite numérique (Un )n 
IN définie par :
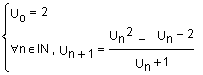
1°) - Calculer les quatre premiers termes de cette suite. ( 1 pt )
2°) - a) Montrer que (Un )n IN est une suite arithmétique dont on précisera la raison. ( 1 pt )
b) Exprimer Un en fonction de n. ( 0,5 pt )
c) Quel est le sens de variation de (Un )n IN ? ( 0,25 pt)
3°) - Pour tout n IN, on pose Vn = e2(1 – n).
a) Montrer que (Vn)n IN est une suite géométrique dont on précisera le premier terme et la raison. ( 1 pt )
b) Calculer la limite de Vn quand n 
+ 
. ( 0,25 pt)
EXERCICE 2 ( 4 points ) corrigé
Le tableau suivant indique l’évolution de l’effectif d’un Collège au cours des huit dernières années.
(xi désigne le rang de l’année et yi l’effectif correspondant).
|
Année |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
yi |
370 |
360 |
380 |
410 |
420 |
440 |
450 |
470 |
1°) - Représenter le nuage de points Mi (xi, yi) associé à cette série statistique dans un repère orthogonal.
- Sur l’axe des abscisses, prendre 1 cm pour unité graphique. ( 0,75 pt )
- Sur l’axe des ordonnées, placer 350 à l’origine puis choisir 1 cm pour représenter 10 élèves.
2°) - Calculer les coordonnées du point moyen G. ( 0,5 pt )
3°) - On note (S1) la série statistique allant de 1994 à 1997 et (S2) la série allant de 1998 à 2001.
a) Déterminer les coordonnées des points moyens respectifs G1 et G2 des séries (S1) et (S2). (0,5 + 0,5 pt)
b) Déterminer une équation cartésienne de la droite (D) passant par G1 et G2. ( 0,75 pt )
c) Construire cette droite (D). Que représente-t-elle ? (0,25 + 0,25 pt)
d) En déduire une estimation de l’effectif du collège en 2003. ( 0,5 pt )
PROBLEME : ( 12 points ) corrigé
On considère la fonction numérique f définie par : f(x) = 2 ln x (ln x – 1). On note (C ) la courbe représentative de f dans un plan rapporté à un repère orthonormé (O ;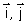 
) d’unité 1 cm.
1°) - a) Déterminer l’ensemble de définition Df de f. ( 0,5 pt )
b) Calculer les limites aux bornes de Df. (0,5 + 0,5 pt)
c) Montrer que pour tout x 
Df, f ’(x) = 
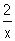(2 ln x – 1). ( 1 pt )
d) Dresser le tableau de variation de f. ( 1 pt )
2°) - a) Déterminer les coordonnées des points d’intersection de (C ) avec l’axe (x’Ox). ( 1 pt )
b) Donner une équation de la tangente (T) à (C ) au point d’abscisse e. ( 1 pt )
c) Montrer que (C ) admet un point d’inflexion I dont on déterminera les coordonnées. ( 1 pt )
3°) - a) Etudier les branches infinies de (C ) (on admet que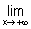 
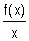= 0). (0,25 + 0,25 pt)
b) Calculer f (e–1) et f (e2). ( 0,5 + 0,5 pt )
c) Construire (T) et (C ). ( 0,5 + 1,5 pt )
4°) - Soit F la fonction définie par F(x) = 2x (ln x)2 – 6x ln x + 6x.
a) Montrer que F est une primitive de f sur Df. ( 1 pt )
b) Calculer, en cm2, l’aire A du domaine plan limité par(C ), l’axe (x’Ox) et les droites d’équations x = 1 et x = e. ( 1 pt )
On donne :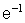 
≈ 0,4 ; 
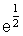≈ 1,7 ; e ≈ 2,7 ; 
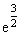≈ 4,5 ; e2 ≈ 7,4.