Enoncé Mathématiques série A 2007
Baccalauréat de l'enseignement général
Madagascar
Session 2007
mathematiques – Série : A
NB : - Le candidat doit traiter les DEUX Exercices et le PROBLEME
- Machine à calculer autorisée
EXERCICE I (5 points) corrigé
Soient 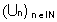 et
et 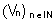 deux suites numériques définies respectivement par :
deux suites numériques définies respectivement par :
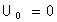
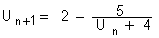 , n
, n IN et
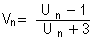 , n
, n IN
1- Calculer U1, V0 et V1. (0,25x3pts)
2- a- Montrer que 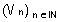 est une suite géométrique de raison
est une suite géométrique de raison 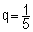 (1pt)
(1pt)
b- Exprimer Vn en fonction de n. (1pt)
3- a- Exprimer Un en fonction de Vn . (1pt)
b- En déduire l’expression de Un en fonction de n. (0,5pt)
c- Calculer 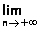 Un. Que peut-on en conclure ? (0,5+0,25pt)
Un. Que peut-on en conclure ? (0,5+0,25pt)
EXERCICE II (5 points) corrigé
Un sac contient 10 boules indiscernables au toucher, portant les lettres A, B et C et dont la répartition
suivant la couleur est donnée par le tableau ci-dessous :
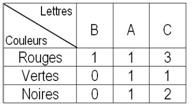
Chaque boule a la même probabilité d’être tirée.
1°-On tire au hasard et simultanément trois boules du sac.
a-Déterminer le nombre de tirages possibles. (0,5pt)
b-Calculer la probabilité de chacun des évènements suivants :
E1 :‘‘obtenir trois boules de même couleur’’. (1pt)
E2 :‘‘obtenir exactement deux boules portant la même lettre ’’. (1pt)
E3 :‘‘obtenir trois boules de même couleur et portant la même lettre’’ (0,5pt)
2°-On tire successivement trois boules du sac, sans remettre dans le sac la boule qui a été tirée.
Calculer la probabilité des évènements suivants :
F1 :‘‘obtenir les lettres B, A et C dans cet ordre ’’. (1pt)
F2 :‘‘obtenir au plus deux boules noires’’. (1pt)
(N.B : Mettre les résultats sous-forme de fractions irréductibles)
PROBLEME (10 points) corrigé
Soit la fonction numérique f de la variable réelle x définie sur IR par : 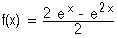 .
.
On désigne par (C ) sa courbe représentative dans un repère orthonormé direct (O ;  ) d’unité 2cm.
) d’unité 2cm.
1-Calculer 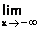 f(x). Interpréter géométriquement le résultat. (0,5+0,5) (0,5+0,5)
f(x). Interpréter géométriquement le résultat. (0,5+0,5) (0,5+0,5)
2-Montrer que pour tout x IR , f(x) =
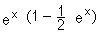 et en déduire
et en déduire 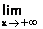 f(x). (0,5+0,5) (0,5+0,5)
f(x). (0,5+0,5) (0,5+0,5)
3-a-Déterminer la fonction dérivée f ’(x) et montrer que pour tout x IR, f ’(x) = e x (1 – e x ) (1+0,5) (0,5+0,5)
b-Etudier le signe de f ’(x), pour tout x IR. (0,5) (0,5)
c-En déduire le tableau de variation de f. (1,5) (1)
4-a-Déterminer les coordonnées du point A intersection de la courbe (C ) avec l’axe des abscisses. (1) (0,5)
b-Ecrire une équation de la tangente (T) au point d’abscisse xo = ln 2. (1) (0,5)
5-En remarquant que pour tout x IR :
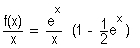
Calculer 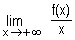 . Interpréter géométriquement le résultat. (On admet que
. Interpréter géométriquement le résultat. (On admet que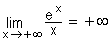 ) (0,5+0,5) (0,5+0,5)
) (0,5+0,5) (0,5+0,5)
6-Tracer la courbe (C ) et la tangente ( T ). (1+0,5) (1+0,5)
Pour A2 seulement :
7-a-Montrer que pour tout x IR. f(x)
 (0, 0) (0,5)
(0, 0) (0,5)
b-Déterminer une primitive de f sur IR. ( 0 ) (0,5)
c-En déduire l’aire géométrique A, en cm2, du domaine plan limité par la courbe (C ),
l’axe des abscisses et les droites d’équations : x = 0 et x = ln 2. ( 0 ) (1)
On donne ln 2 = 0,7 ; e = 2,7