Série C - Mathématiques

Baccalauréat de l'enseignement général

Madagascar

Session 2005

 

Matière    –  Série : C

 

N. B :    - L’Exercice et les DEUX Problèmes sont obligatoires.

- Machine à calculer autorisée.

 

EXERCICE                 (4 points)

1°)     On donne l’équation : 2x – y = 1    (1).

 x  et  y étant les inconnues, x  et  y sont des entiers relatifs.

a/ Trouver une solution particulière (x₀, y₀) de cette équation.                                    (0,25pt)

b/ Résoudre dans  Z x  Z l’équation (1).                                                                 (0,75pt)

2°)     Un entier naturel A est tel que :

- dans la base 10,  A s’écrit :  A = b + 6.

- dans le système binaire, A s’écrit : A = (1a1)₂.

Trouver une relation qui lie a et b.                                                                    (0,50pt)

3°)     Résoudre dans IN² le système à deux inconnues x  et  y suivant :

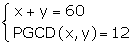                                                                             (0,50pt)

4°)     Deux urnes identiques U₁ et U₂ contiennent chacune :

- deux boules numérotées chacune 0.

- trois  boules numérotées chacune 1.

- une boule numérotée 2.

On tire au hasard une boule de U₁ puis on extrait au hasard et simultanément deux boules de U₂.

a/ Calculer la probabilité de chacun des événements suivants :

A : « Les boules obtenues portent le même numéro ».                                         (0,50pt)

B : « La somme des numéros notés est égale à 4 ».                                           (0,50pt)

b/ Soient  x  le numéro de la première boule tirée et  y  la somme des numéros des boules obtenues au deuxième tirage. Calculer la probabilité de l’événement :

C : « Le couple (x , y)  est solution de l’équation 2x – y = 1 ».                               (1,00pt)

 

 

PROBLEME 1           (7 points)

Soit  (ABC) un triangle isocèle et rectangle en A avec AB = AC = 4cm et 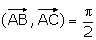. Soient  I, J et K  les milieux respectifs des segments  [ AB ] , [ BC ]  et  [ CA ]  et  E le symétrique de A par rapport à J.

PARTIE 1

1°)  a/ Montrer que 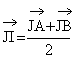   et 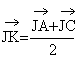        . En déduire que 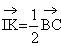.             (0,25+0,25pt)

b/ Montrer que 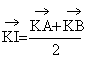   et 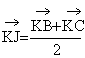  .  En déduire que 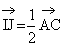.       (0,25+0,25pt)

c/ Montrer que le quadruplet (AIJK) est un carré. Faites une figure.                    (0,25+0,50pt)

2°) Soit r la rotation de centre  J et d’angle 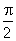 et  t la translation de vecteur  .

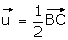a/ Déterminer l’image du point  I par  t  et celle de K par r.                              (0,25+0,25pt)

b/ Déterminer l’image de  I  par  f = rot.

En déduire la nature et les éléments caractéristiques de f.                                      (0,25+0,25pt)

c/ Soit g = tor. Déterminer l’image de K par g.                                               (0,50pt)

En déduire la nature et les éléments caractéristiques de g.                                     (0,25pt)

3°)  Soit S la similitude plane directe qui transforme B en E et J en C.

Préciser le rapport et l’angle de S.                                                               (0,50+0,50pt)

         N.B. : Justifier votre réponse.

 

PARTIE 2

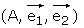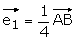Le plan complexe est rapporté à un repère orthonormé où  et .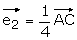

Dans ce repère, on donne les points : A(0, 0), B(4, 0) et C(0, 4).

1°) Préciser les coordonnées des points E et J.                                                             (0,25pt)

2°) a/ Donner l’écriture complexe de S. (S étant la similitude plane directe donnée dans la PARTIE 1, 3°).                                                                                                                     (1,00pt)

b/ En déduire les coordonnées du centre de S.                                                     (0,50pt)

3°) Soit la transformation S = SoS_(AB), où S_(AB) est la symétrie orthogonale par rapport à la droite (AB).

a/ Préciser la nature et les éléments caractéristiques de  S.                                       (0,25pt)

b/ Déterminer l’écriture complexe associée à S.                                                       (0,50pt)

 

 

PROBLEME 2           (9 points)

Soit la fonction numérique f définie sur 3 par : f(x) =.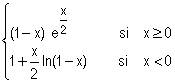

(C) sa représentation graphique dans un plan affine rapporté à un repère orthonormé (O,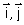)  (unité : 2cm).

PARTIE A

1°) Soit g la fonction définie sur l’intervalle ]-∞ , 0 [ par :   g(x) = (1 – x) ln(1 – x ) – x.

a/ Etudier les variations de g et dresser son tableau de variation.                                (1,50pt)

b/ En déduire le signe de g(x) suivant les valeurs de x.                                             (0,25pt)

2°)  a/ Montrer que f est continue en x₀ = 0.                                                               (0,25pt)

b/ Calculer 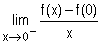.                                                                                 (0,25pt)

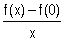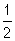
c/ Pour  x  > 0 , montrer qu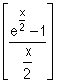e :          =            – e.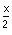

Calculer 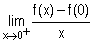.    (Indication : poser   X 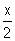₌).                                     (0,50+0,25pt)

d/ En utilisant les résultats de b/ et c/, quelles conclusions peut-on tirer sur f puis sur (C) ?        (0,50pt)

3°) a/ Calculer 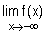  et 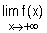 .                                                                  (0,25+0,25pt)

b/ Pour tout x élément de l’intervalle ] -∞ , 0 [ ,  montrer que : f’(x) = 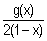.            (0,25pt)

c/ Pour tout x élément de l’intervalle ] 0 , +∞ [ , calculer f’(x).                                   (0,50pt)

d/ Dresser le tableau de variation de f.                                                                  (0,50pt)

4°) Etudier les branches infinies de (C).                                                             (0,25+0,25pt)

5°) Montrer que la courbe (C) coupe l’axe des abscisses en deux points distincts d’abscisses respectives  1 et    avec  –2 < < –1.                                                                             (0,25+0,50pt)

6°) Tracer la courbe (C) en précisant les demi-tangentes à l’origine O du repère.        (0,75+0,25pt)

7°) Calculer, en cm², l’aire A du domaine plan limité par (C), l’axe des abscisses et les droites d’équation x = 0 et x = 1.                                                                                                                     (0,25pt)

 

PARTIE B

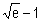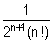
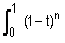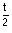Soit (I _n)_nIN la suite définie par : I₀=   et pour tout n IN*, I_n =  e dt.

1°) A l’aide d’une intégration par parties, calculer  I ₁ .                                                     (0,25pt)

2°) Montrer que pour tout n élément de IN, on a  I_{n+1 =} I_{n –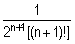} .                          (0,50pt)

3°) En déduire par récurrence que, pour tout entier naturel n on a :

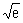= 1+ 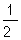.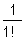+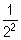.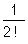+ …+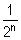.+I_n.                                                     (0,25pt)

4°) Donner alors l’expression de I_n en fonction de n.                                                      (0,25pt)

On donne :             ln 2 ≈ 0,7               ln 3 ≈ 1,1 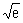              ≈ 1,6