Enoncé Mathématiques série C 2011
Résumé de section
-
Nous mettons à votre disposition des sujets de Mathématiques
proposés au baccalauréat série C à Madagascar
Baccalauréat de l'enseignement général
Madagascar
Session 2011
MATHEMATIQUES – Série : C
N.B : - L’ exercice et les DEUX Problèmes sont obligatoires.
- Machine à calculer scientifique non programmable autorisée
EXERCICE (4 points)
A- Probabilité corrigé
On dispose d’un dé cubique parfait dont les faces sont numérotées : 0, 1, 1, 2, 2 et 2.
1- On lance une fois ce dé. Calculer les probabilités P0 , P1, P2 d’apparition respective des faces
numérotées 0, 1, 2. (0,25pt x3)
2- Une épreuve consiste à lancer trois fois de suite ce dé et d’une manière indépendante.
On note chaque fois le numéro obtenu sur la face supérieure de ce dé.
Calculer la probabilité de chacun des événements suivants :
A : « La somme des numéros obtenus est égale à 4 ». (0,25pt)
B : « Obtenir exactement deux fois le numéro 1 ». (0,5pt)
C : « Obtenir chacun des trois numéros différents lors des 3 lancers ». (0,5pt)
NB : on donnera les résultats sous forme de fraction irréductible
B- Arithmétique corrigé
1- a) Convertir dans la base 10 l’entier a écrit dans le système binaire : a =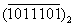 
. (0,25pt)
b) Convertir dans le système binaire l’entier naturel b = 54 de la base 10. (0,25pt)
2- a) Dresser la table d’addition et de multiplication de Z/ 5Z. (0,25pt+0,25pt)
b) Résoudre dans Z/ 5Z x Z/ 5Zle système :
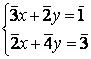(0,5pt)
c) Résoudre l’équation :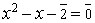 
dans Z/ 5Z. (0,5pt)
PROBLEME 1 (7 points) corrigé
ABEC est un losange de centre 0 dans un plan orienté ( P ) tel que
AB = AC = BC = 4 cm et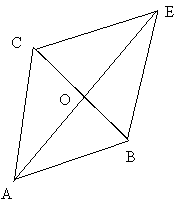 
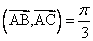
Les parties A et B sont indépendantes.
Partie A :
1- Reproduire cette figure en vraie grandeur. ( 0,5pt)
2 - a) On considere le système de points pondérés J=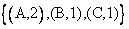
.
Montrer que ce systéme admet un barycentre G et que G est le milieu du segment [OA] (0,25pt+0,25pt)
b) Montrer que le vecteur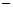 
2
+
+
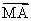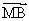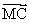où M est un point variable, est un vecteur
constant que l’on déterminera. (0,5pt) (0 ;5)
c) Déterminer et représenter l’ensemble (D) des points M du plan (P) vérifiant :
(
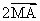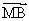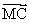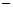
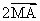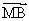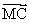++) (++) = 0 (0,5pt)
3 - Soit S la similitude plane directe de rapport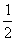 
, d’angle 
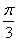et qui transforme A en B.
On note I le centre de S et I’ son image par la symétrie centrale SB de centre B.
a) Montrer que le triangle IAI’ est un triangle équilatéral de sens direct. (0,5pt)
b) Montrer que (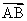
,
) = 
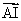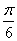(0,5pt)
c) Placer alors les points I et I’ (0,5pt)
Partie B : Utilisation des nombres complexes.
On rapporte le plan (P) au repère orthonormé direct (A,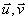
) avec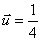 
(
).
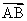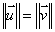1-a) Donner les affixes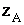 
et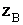 
respectives de A et B. (0,25pt + 0,25pt)
b) Donner le module et un argument de l’affixe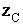 
de C et en déduire l’affixe 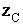sous forme
algébrique. (0,25pt + 0,25pt + 0,25pt)
c) Calculer l’affixe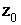 
de O. (0,25pt)
2-a) Donner l’expression complexe de la similitude directe S de rapport 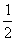et d’angle,
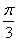qui transforme A en B. (0,5pt)
b) En déduire l’affixe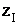 
du centre I de S. (0,5pt)
c) Vérifier que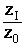 
est un nombre réel et que 
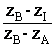est imaginaire pur. (0,25pt+0,25pt)
d) Que peut- on en déduire pour les points I, O et A d’une part et pour les droites (IB) et
(AB) d’autre part. (0,25pt+ 0,25pt)
PROBLEME 2 ( 9 points) corrigé
Soit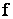 
la fonction numérique définie sur IR par : 
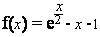. On désigne par (C) sa courbe
représentative dans un repère orthonormé (0,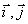
) d’unité 2cm.
Partie A : Etude de la fonction f.
1- Calculer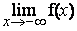 
et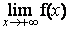 
(0,25pt + 0,25pt)
(Pour la limite en +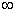
, poser X=
)
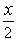2- a) Etudier les variations de f. (0,75pt)
b) Montrer que la droite (D) d’équation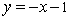 
est asymptote à (C), (0,75pt)
c) Montrer que l’équation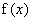 
= 0 admet pour solutions O et 
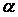dans IR et 2<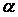<3 (0,25pt+0,5pt)
3 - Tracer (C), et (D) dans un même repère. (1pt+ 0,5pt)
On donne e = 2,7 ;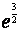 
= 4,48 et pour construction, on prendra 
.
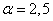4 - Soit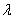 
un nombre réel strictement inférieur à 
.
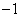a) Exprimer en fonction de 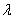l’aire A (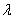), en cm2, de la portion du plan délimitée par la courbe (C),
la droite (D) et les droites d’équations respectives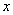 
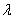= et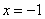 
. (0,5pt)
b) Calculer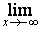
. (0,5pt)
Partie B : Etude d’une suite.
On considère la fonction numérique g définie su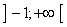r 
par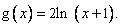 
1 - Etudier les variations de la fonction g.
(0,75pt)
2 - Montrer que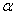 
est solution de l’équation
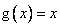. (0,5pt)
3 - Montrer que pour tout x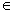
, 
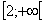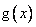
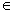
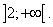(0, 5pt)
4 - (Un) n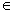IN est la suite numérique définie par U0 = 3 et Un+1= g(Un) n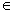IN et que tous les
termes de la suite appartiennent à 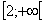.(on ne demande pas de le démontrer ).
a) Démontrer que pour tout x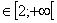
, on a 
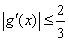. (0,5pt)
b)Démontrer, en utilisant les théorèmes des inégalités des accroissements finis, que pour tout n 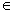IN, on a : 
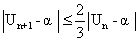et que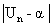 
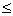
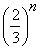. (0,25pt + 0,25pt)
c)Prouver que la suite (U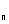
) converge vers un réel l que l’on précisera. (0,5pt)
d)Déterminer l’entier naturel p tel que, pour tout entier naturel n supérieur ou égal à p on ait :
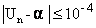. (0,5pt)