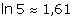Enoncé Mathématiques série C 2012
Baccalauréat de l'enseignement général
Madagascar
Session 2012
MATHEMATIQUES – Série : C
NB : - L’exercice et les deux problèmes sont obligatoires
- Machine à calculer scientifique non programmable autorisée.
Exercice : (4 points)
1 - On considère, dans Z x Z, l’équation définie par : (E) : 11x -7y = 9.
On note par (x0 , y0) la solution de cette équation.
a) Montrer que :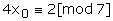 
(0,5)
b) En déduire une solution particulière de l’équation (E). (0,25)
c) Résoudre dans Z x Z l’équation (E). (0,75)
d) Trouver un couple (a , b) 
Z x Z vérifiant : 11a – 7b = 9 = PGCD ( a ; b). (0,5)
2- On dispose d’un dé cubique parfait à six faces numérotées 2, 3, 4 dont une face marquée 2, trois faces marquées 3 et deux faces marquées 4.
On lance trois fois de suite ce dé. On note chaque fois le numéro apparu à la face supérieure, en l’écrivant dans l’ordre de gauche à droite pour former un nombre entier naturel.
Calculer la probabilité de chaque événement suivant :
- A : « Le nombre formé ne contient que des chiffres premiers ». (0,5)
- B : « le chiffre 4 apparaît au moins une fois dans le nombre formé ». (0,5)
- C : « Obtenir l’écriture du nombre 92 dans le système à base 5 ». (0,5)
- D : « La somme des chiffres dans le nombre formé est 8 ». (0,5)
NB : On donnera les résultats sous forme de fraction irréductible.
Problème 1 : (7 points)
On considère dans le plan P un triangle rectangle et isocèle ABC tel que AB=AC=2
(unité graphique : 2cm) et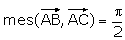
.
On désigne par G le milieu du segment [BC] et par O celui de [AC]. On met les points A et C sur une droite horizontale.
Partie I :
1- a- Déterminer et construire le barycentre F des points A, B et C affectés respectivement de 2, -1 et 1. Montrer que ABGF est un parallélogramme. (0,25+0,5+0,25)
b- Déterminer et construire l’ensemble (E) des points M du plan P tel que :
||
|| = || 
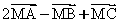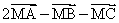||. (0,75 + 0,25)
2- On appelle J le symétrie de B par rapport à A et (D) la droite passant par J et parallèle à (AC).
Soit (
) l’ensemble des points M du plan P tel que, si H est le projeté orthogonal de M sur (D) alors l’équation de () est : 2MA2 – MB2 + MC2 = MH2 – 4 (1)
a- Montrer que () passe par A et C. (0,5)
b- Calculer FA2, FB2 et FC2. (0,5)
c- Démontrer que l’équation (1) est équivalente à l’équation 2MF2 = MH2.
En déduire la nature de (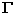). (0,75 + 0,25)
Partie II : Le plan P est rapporté au repère orthonormé direct (O,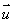 
, 
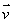) tel que = 
.
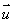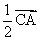1- Déterminer respectivement les affixes zC , zJ et zF des points C, J et F. (0,5)
2- On considère une similitude plane indirecte S qui, à tout point M d’affixe z associe le point M’ d’affixe z’.
a- Sachant que S transforme F en J et laisse invariant C, donner l’expression complexe de S. (0,5)
b- En déduire les éléments caractéristiques de S. (0,75)
3 - a- Calculer les affixes des points A’ = S(A) et B’ = S(B). (0,5)
b- Construire dans le même plan P, l’image par S du triangle ABC. (0,75)
Problème 2 : (9 points)
NB : Les parties A et B sont indépendantes.
Partie A :
On considère la fonction f définie sur IR par :
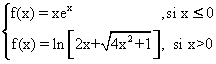
1 - a) Etudier la continuité de f en x0 = 0. (0,25)
b) En admettant que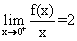 
, étudier la dérivabilité de f en x0 = 0. (0,25)
2 - Etudier les variations de f en dressant son tableau de variation. (1)
3 - Soit g la fonction définie sur [2 ; +∞[ par : g(x) = x – f(x).
a) Montrer que, pour tout x [2 ; +∞[ , g’(x) > 0. (0,5)
b) Prouver que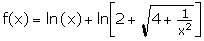 
, pour x >0.
En déduire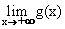 
(0,25 + 0,25)
c) Déduire le tableau de variation de g. En déduire que l’équation f(x) = x admet une solution α et une seule, telle que 2≤ α≤3. (0,25 + 0,5)
4 - Soit l’intervalle I= [2 ; 3].
a) Démontrer que , si x I alors f(x) I. (On pourra utiliser A-2). (0,5)
b) Prouver que pour tout x I, on a : 
.
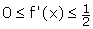En déduire que : | f(x) – α | ≤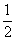
| x – α |, pour x I. (0,5 + 0,25)
5 -Soit la suite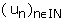 
définie par :
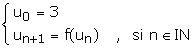
a) Démontrer, par récurrence, que un I, pour tout n IN. (0,25)
b) Montrer que, pour tout n , |un+1 – 
|≤
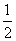|un - | et |un - |≤ 
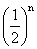. (0,25 + 0,25)
c) En déduire que la suite (un) converge vers le nombre réel . (0,25)
d) Déterminer n0 pour que u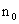
soit une valeur approchée de à 0,1 près.
Calculer u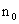. (0,25 + 0,25)
6 - On appelle (C) la courbe représentative de f dans un repère orthonormé ( 0,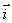 
, 
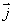) d’unité : 2cm.
a) Etudier les branches infinies de (C) (0,25)
b) Tracer (C) et la droite (D) : y = x , en précisant et les demi-tangentes à (C) en x0 = 0. (0,75)
Partie B :
On considère l’équation différentielle : (E1) : y’ – y = xex.
1- Résoudre l’équation différentielle (E2) : y’ – y = 0. (0,5)
2- Soient a et b deux réels et u la fonction définie sur IR par : u(x) = (ax + b)ex.
a) Déterminer a et b pour que u soit solution de (E1). (0,25)
b) φ étant une fonction dérivable sur IR. Montrer que (φ +u ) est une solution de (E1) si et seulement si φ est une solution de (E2). (0,5)
c) En déduire l’ensemble des solutions de (E1). (0,25)
3- Déterminer la solution de (E1) qui s’annule en 0. (0,5)
On donne :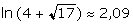 
; 
; 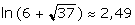