Contrainte en un point :tenseur des contrainte (B+1,B+2)
Résumé de section
Contraintes autour d’un point
Avertissement : l’intention de ce cours est de donner quelques notions sur l’évaluation d’une contrainte en un point d’un solide suivant l’orientation de la surface (ou « facette ») passant par ce point. En effet, suivant une direction, la contrainte peut être normale (ou « principale ») et de cisaillement suivant une autre. Il faut pouvoir l’évaluer dans toutes les directions. L’une ou l’autre pouvant être déterminante pour vérifier la résistance du solide.
Toutes ces notions intègrent maintenant les logiciels modernes. Le calculateur- projeteur doit comprendre le sens des résultats donnés par sa machine afin de pouvoir utiliser ces outils dans les meilleures conditions.
L’esprit de ce cours proposé est analogue dans la démarche à celui présenté par Yves Debard enseignant en IUT et auteur du logiciel « RDM6 ». Ce cours est une aide à l’utilisation de ce logiciel gratuit bien adapté à l’enseignement de la R.D.M.
Ce travail n’est qu’une amorce d’un long travail d’élaboration de cours qui devrait aboutir en 2014 ! Mais une bonne partie du logiciel peut être déjà utilisé en s’aidant des documents déjà installés dans la médiathèque.
PB Janvier 2012
I –Notion de contrainte, objectifs de l’étude proposée :
1-La pression d’un fluide est une contrainte:
Insufflons de l’air dans une enveloppe élastique d’égale épaisseur. L’enveloppe se déforme et prend une forme sphérique. La forme de l’enveloppe suggère que des forces s’exercent sur la paroi selon une direction normale à celle-ci. Ces forces sont réparties uniformément sur la surface. Nous dirons que le gaz exerce une pression sur la paroi ou une contrainte ici normale en tout point de la surface.
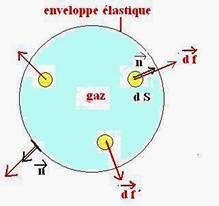
2-Définition de la pression en un point M:
La pression exercée sur l’enveloppe est variable en direction, il faut donc pour la définir, considérer un petit élément de surface dS autour du point M sur lequel la force exercée dF peut être considérée constante.
La pression est le quotient de la force locale par l’élément de surface dS de normale orientée vers l’extérieur n. L’orientation de la normale permet d’attribuer un signe à la pression.

3-Analogie avec la contrainte :
Toute surface plongée dans un fluide (liquide ou gaz) est soumise a une pression c'est-à-dire à une contrainte normale quelle que soit l’orientation de celle-ci. Dans ce cas, l’état de contrainte est dit sphérique ou « hydrostatique ».
Dans un solide soumis à diverses sollicitations internes, c’est un peu plus compliqué : la contrainte en un point dans une direction donnée possède en général une composante tangentielle (ou de cission) et une composante normale à l’élément de surface. Néanmoins, comme nous le verrons, il existe toujours des directions particulières selon lesquelles les contraintes sont purement normales. La recherche de ces directions fait partie des objectifs de cette étude car elles sont déterminantes pour évaluer la résistance du matériau.
L’unité l’égale de contrainte est donc le pascal .
Remarque : La pression atmosphérique est voisine de 100.000 Pa, on conçoit que le pascal représente une très petite contrainte. On utilise en RDM avantageusement les multiples du pascal : MPa=106Pa ; GPa=109Pa
II-La contrainte en un point d’un solide:
(Le symbole de la contrainte le plus utilisé est la lettre « sigma » soit s en minuscule ou S en majuscule.) .
1-Définition du vecteur contrainte en un point :
En chaque point d’un solide soumis à des forces extérieures, des forces intérieures ou de cohésion prennent naissance. Pour accéder à ces forces par le calcul il est commode de réaliser des coupures fictives de section S à travers ce solide.
Cette section S partage le solide en deux parties A et B
On détermine alors les forces intérieures au niveau de chaque coupure en écrivant que la partie A est en équilibre sous l’action des forces extérieures de gauche et des forces intérieures existantes au niveau de la coupure.
Ces forces de cohésion uniformément réparties sur la surface S sont regroupées en une force résultante (RG) et un moment fléchissant (MG): Les composantes de RG et MG au nombre de 6 dans le cas le plus général constituent les éléments du torseur dit de cohésion au niveau de la coupure.
Cette détermination du torseur de cohésion est une première étape dans l’évaluation de la contrainte. Il faut ensuite calculer les composantes du vecteur contrainte suivant le point considéré et suivant la direction de la section.
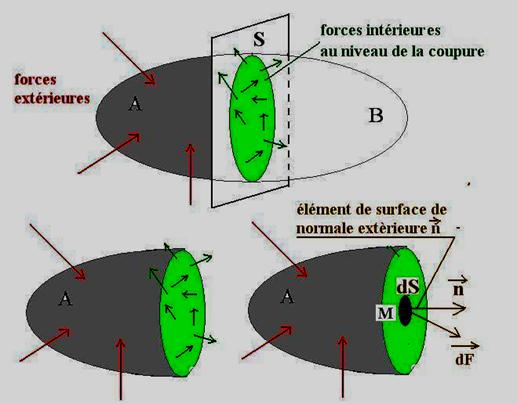
La contrainte étant une grandeur généralement variable à l’intérieur de la section S, il faut la définir sur un petit élément de surface dS entourant le point.
Considérons donc un point M de la section .Soit dS un petit élément de cette section entourant M. Soit n un vecteur unitaire d’origine M, perpendiculaire à cet élément dS et orienté vers l’extérieur de la partie A. Le vecteur n est appelé « vecteur normal » à l’élément de surface.
Nous appellerons l’élément de surface « facette n en M ».
Soit dF le vecteur force de direction quelconque qui agit sur cette facette.
La contrainte en M sur la facette n est le vecteur :
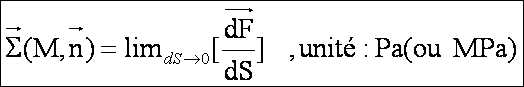
La contrainte en M est ainsi la force par unité de surface d’effort de cohésion en M.
Au final, c’est la contrainte dans le matériau qui est déterminante pour évaluer sa résistance. (et non les sollicitations auxquelles il est soumis : force, moment qui entrent en jeu cependant pour l’évaluer)
La valeur et la nature de la contrainte sur le matériau (contrainte normale, contrainte tangentielle) sont essentielles pour prévoir la bonne tenue du matériau dans le temps. La résistance du matériau consiste à calculer la contrainte à laquelle il est soumis et de vérifier que celle-ci ne dépasse pas une contrainte limite en dessous de laquelle le matériau conserve ses propriétés (limites d’élasticité, de plasticité)
2-Composantes tangentielle et normale du vecteur contrainte:
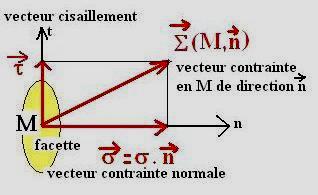
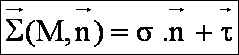
La valeur de la projection du vecteur contrainte sur la normale est le scalaire:
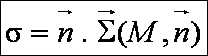
Avec les conventions de signe suivantes :
s >0 contrainte de traction, s<0 contrainte de compression.
3- Etat de contrainte entourant un point : matrice (ou tenseur) des contraintes relative à un repère Mxyz.
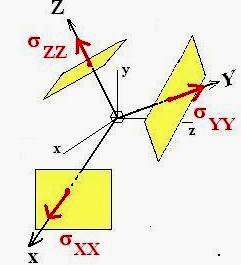
Pour définir complètement l’état de contrainte en un point M au sein d’un solide, indépendamment de l’orientation n de la facette considérée en ce point, considérons un repère Mxyz orthonormé centré en M dont les axes sont parallèles aux arêtes d’un cube élémentaire.
Le cube est constitué de 6 facettes de dimension suffisamment petites pour considérer le vecteur contrainte associé à chacune des normales comme constant sur toute l’étendue de la face.
Les vecteurs unitaires i , j , k associés à ce repère définissent en M, 3 facettes perpendiculaires entre-elles (représentées espacées pour plus de clarté sur la figure ci-dessous).
Remarque : il est inutile de prendre en compte les vecteurs contraintes sur les faces opposées à celles représentées. La condition d’équilibre de chaque facette impose que le vecteur sur une face « arrière » est égal à l’opposé du vecteur sur la face « avant »
![]()
Donnons les expressions des vecteurs contraintes qui s’exercent sur chaque face en fonction de leurs composantes dans le repère Mxyz.
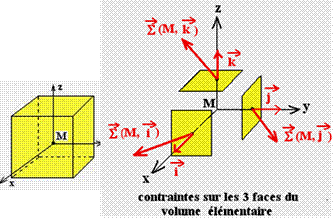
Remarque : sur la facette i la contrainte normale (grandeur scalaire) est :
![]()
Et le vecteur cisaillement est égal à :
![]()
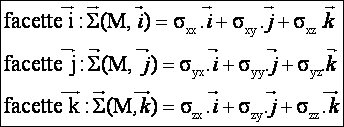
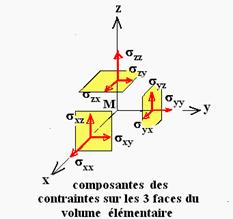
Les indices caractérisent une composante particulière :
sxx , syy, szz désignent les composantes normales des contraintes respectivement dans les directions x, y et z .
sxy et sxz désignent les deux composantes tangentielles ou de cission de la facette i, la première parallèle à l’axe y et la deuxième parallèle à z.
syx et syz désignent les deux composantes tangentielles ou de cission de la facette j,la première parallèle à l’axe x et la deuxième parallèle à z.
szx et szy désignent les deux composantes tangentielles de la facette k, la première parallèle à l’axe x et la deuxième parallèle à y.
Ces 9 composantes peuvent être rassemblées dans une matrice :
Nous pouvons définir la matrice des contraintes relative au repère Mxyz
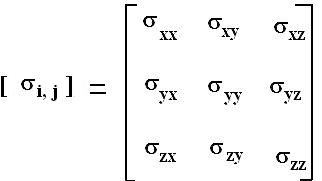
Principe de réciprocité des contraintes tangentielles :
Les composantes tangentielles telles que sxy et syx sur les facettes verticales du cube élémentaire créent des couples antagonistes avec les composantes tangentielles des faces opposées (voir schéma ci-dessous).Ces couples doivent s’équilibrer pour éviter la mise en rotation du cube autour de Mz.
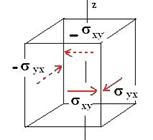
Par conséquent les composantes tangentielles perpendiculaires à Mz ont la même valeur :
sxy=syx
Un raisonnement analogue pour les axes Mx et My conduit à écrire:
sxz=szx ; syz=szy
Ces différentes égalités constituent le principe de réciprocité des contraintes tangentielles. Sa conséquence est très importante pour la matrice des contraintes
Ainsi, la matrice s ij caractérisant l’état de contrainte en M relativement à tout repère quelconque Mxyz est donc symétrique par rapport à la diagonale.
Nombre de composantes inconnues de l’état de contrainte :
Dans le cas le plus général l’état de contrainte est défini par 6 termes : les 3 composantes de la diagonale et les 3 composantes situé au-dessus (ou en dessous) de la diagonale.
La matrice étant symétrique, il est toujours possible de réduire ce nombre à trois en réalisant un changement de repère (remplacement des axes Mxyz par MXYZ appelés « axes principaux »). Dans ce cas, la matrice est diagonale : les seules inconnues étant sXX, sYY, sZZ appelées contraintes principales. Relativement aux axes principaux les composantes tangentielles sont nulles.
Comme nous le verrons, la détermination de ces contraintes principales est fondamentale pour vérifier la bonne tenue du matériau.
Dans bien des cas ce nombre peut être encore réduit :
Dans le cas d’une pièce plane (absence de composante suivant z), il ne subsiste relativement à un repère quelconque que 3 inconnues sxx syy et sxy.
Dans le cas d’une pièce soumise à une traction (ou compression) pure selon Mx, ou un cisaillement pur selon My, l’état de contrainte est caractérisé par une seule inconnue :
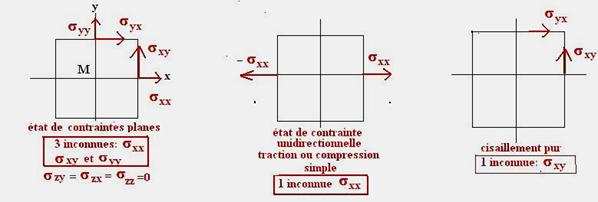
III Vecteur contrainte S(M,n)sur une facette orientée dans une direction quelconque du repère Mxyz:
a-expression du vecteur en fonction des vecteurs contrainte sur les 3 faces du cube élémentaire :
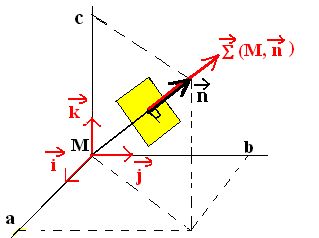
Nous envisageons maintenant d’évaluer la contrainte sur une facette en M de normale n unitaire et de direction quelconque par rapport au repère Mxyz.
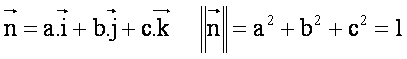
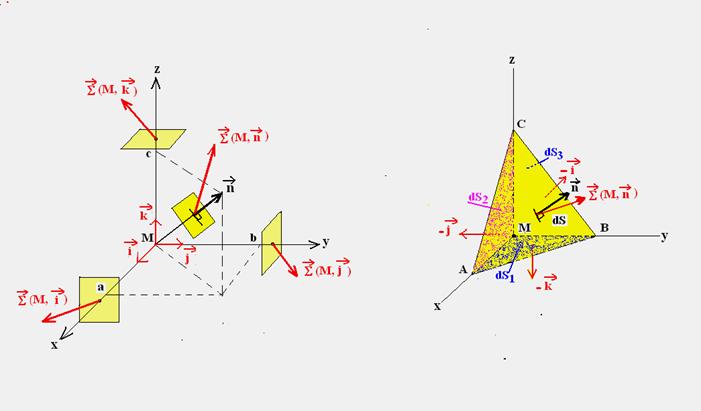
Soient A, B, C les points d’intersection de cette facette (représentée en jaune foncé) avec les axes orthogonaux M,x,y,z. Les points M, A, B et C sont les sommets d’un tétraèdre constitués des 4 facettes triangulaires d’aire infinitésimales respectives notées dS, dS3, dS2, dS1 et de normales extérieures :
![]()
(les facettes dS1, dS2, dS3 étant située en arrière)
Ecrivons que ce tétraèdre est en équilibre sous l’action des forces de contact agissant sur les 4 faces. On négligera le poids de l’élément.
Les vecteurs forces ont même direction et sens que les vecteurs contraintes, ils sont obtenus en réalisant le produit du vecteur contrainte par l’aire élémentaire sur laquelle les forcent s’exercent :
![]()
![]()
![]()
soit, en divisant par dS :
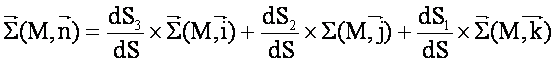
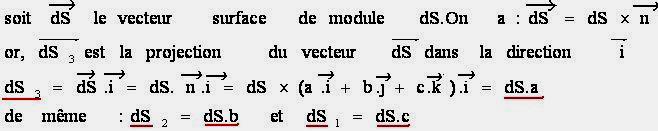
Le vecteur contrainte relatif à la facette n peut s’écrire en fonction des vecteurs contraintes de facettes i, j, k du cube élémentaire (théorème de Cauchy):
![]()
a, b, et c sont les composantes du vecteur normal n à la facette (appelés souvent « cosinus directeurs » de la normale).
b-Expression du vecteur contrainte en fonction de la matrice des contraintes :
Le théorème de Cauchy permet d’écrire :
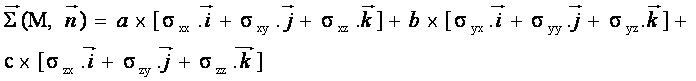
soit, en regroupant les termes en i, j et k, nous obtenons les composantes du vecteur contrainte SX,SY,SZ dans le repère Mxyz en fonction de la matrice des contraintes
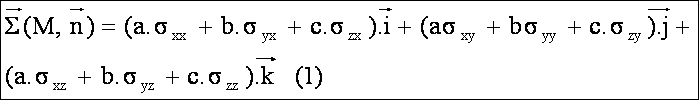
![]()
Ceci conduit à l’écriture matricielle
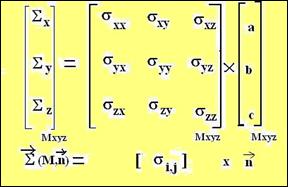
La matrice sij relative au repère Mxyz est la représentation d’un tenseur car cette matrice est un opérateur bi-linéaire qui, appliqué à un vecteur n de R3 donne un autre vecteur S de R3 . L’expression précédente caractérise donc le tenseur des contraintes en M
IV-Contraintes principales et directions principales :
1-Rappel d’un résultat de l’algèbre et définitions :
Comme la matrice [sij] est carrée et symétrique, on démontre en algèbre linéaire que ce type de matrice est diagonalisable, c'est-à-dire que par un changement de base orthogonale approprié :
![]()
Il est toujours possible de trouver un repère MXYZ par rapport auquel la matrice des contraintes ait la forme diagonale suivante :
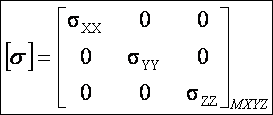
Dans ce cas, les axes du repère orthonormé M, X, Y, Z sont appelés « axes principaux » ou « directions principales » et les contraintes selon ces directions sXX, sYY, sZZ sont les « contraintes principales ».
Dans ce repère MXYZ la matrice n’admet pas de composantes tangentielles…Les seules composantes sXX, sYY, sZZ sont donc normales aux axes principaux X, Y et Z
2-Méthode algébrique (dite des « valeurs propres ») de détermination des contraintes principales sXX, sYY, sZZ et des directions principales:
Pour déterminer celles-ci et les directions des axes X,Y,Z correspondants, écrivons que le vecteur contrainte doit être colinéaire au vecteur normal à une facette dite « principale » n de direction (a,b,c) à déterminer.
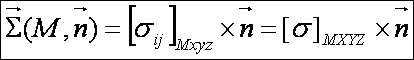
[s]MXYZ est une matrice diagonale que nous pouvons écrire :
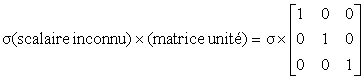
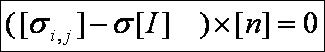
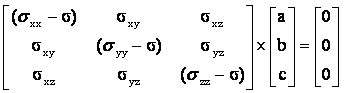
Cette relation matricielle conduit au système (équations dites « aux valeurs propres » de la matrice s ij
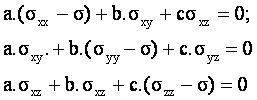
Nous allons vérifier que ce système conduit à la résolution d’une équation du 3ème degré en s admettant 3 solutions sXX, sYY, sZZ appelées valeurs propres de la matrice [sij]. A chaque valeur propre correspond un vecteur propre : nX, nY, nZ orientés dans les directions des axes principaux.
Ce système n’admet de solutions que si le déterminant associé à ce système est nul
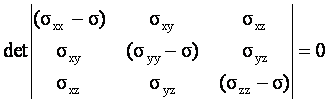
Cette condition conduit à résoudre l’équation du 3ème degré en s :
![]()
Les coefficients ont pour expression en fonction des composantes dans le repère Mxyz:

Et en fonction des contraintes principales :


Remarques :
L’informatique évite les calculs fastidieux
Deux programmes simples inclus dans la médiathèque permettent de gagner beaucoup de temps …
1-La calculette « Graph Calc » permet de résoudre facilement l’équation du 3éme degré.
Ouvrir la rubrique : « tools » puis « équation solver ». Afficher une valeur initiale, le programme affiche alors une 1ère racine la plus proche de la valeur initiale.
Afficher une nouvelle valeur initiale, le programme affiche alors la racine la plus proche de cette nouvelle valeur initiale. Procéder de la même façon pour obtenir la 3éme racine. Etc…..
2-Le logiciel « RDM-6 » effectue le calcul direct des contraintes principales à partir des contraintes relatives à un repère quelconque.
Utiliser le module « rosettes » puis « tenseur des contraintes » . Le logiciel affiche en plus le tri-cercle de Mohr des contraintes.
La détermination des vecteurs propres n consiste à évaluer les coefficients a, b et c (ou « cosinus directeurs ») à partir de chaque valeur propre sXX,sYY,sZZ.
Utiliser pour cela les équations aux valeurs propres ci-dessus.
Il n’est nécessaire forcément des calculer les directions des 3 vecteurs, sachant que ces 3 vecteurs sont orthogonaux.
3-Ces calculs peuvent paraître complexes. La construction graphique de Mohr que nous allons voir maintenant permet de clarifier tout cela et facilite beaucoup la représentation physique d’un état de contrainte.
Conclusion partielle:
A ce stade retenons simplement que pour tout état de contrainte en un point M, aussi complexe qu’il puisse apparaître dans le repère où il est décrit, il existe un repère « central » d’origine M dans lequel les contraintes sont de compression ou de traction pures (les 3 contraintes principales) ; celles-ci agissant selon les 3 directions principales orthogonales . On peut être assuré de l’existence de ces contraintes principales dans tous les cas.
3-Ellipse de Lamé :
Dans le repère principal M,X,Y,Z, le vecteur contrainte de facette n a pour expression , d’après la relation (1) (écrite sur fond de couleur bleue)

Ou a, b et c sont les composantes du vecteur unitaire normal n :
Considérons une rotation d’angle q de la facette dans le plan MXY comme l’indique la figure ci-dessous,
Le vecteur n tournant étant unitaire :
a2+b2=1, soit :
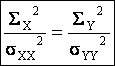
Equation d’une ellipse d’axes MX et MY dans le plan MXY.
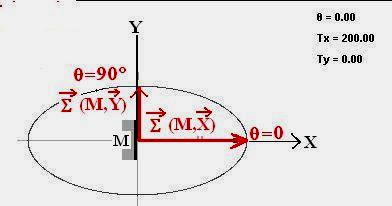
Si l’on considère une rotation quelconque de la facette dans l’espace, l’équation devient :
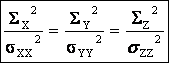
Quand la facette n d’origine M modifie sa direction dans l’espace, l’extrémité du vecteur contrainte se déplace sur l’ellipsoïde dont les axes sont les axes principaux du tenseur des contraintes. Cette ellipse est nommée Ellipsoïde de Lamé.
V –Cercle de Mohr des contraintes :
1-introduction :
La construction du cercle de Mohr est une méthode graphique générale associée à tout tenseur : tenseur des inerties, tenseur des contraintes, tenseur des déformations pour ne citer que ces trois exemples du champ de la R.D.M.
Pour ce que nous traitons dans ce chapitre sa construction permet de déterminer rapidement l’état de contrainte: composantes tangentielle t et normale s du vecteur contrainte en un point M pour toute direction de la facette n dans l’espace.
Nous allons décrire dans un premier temps le cercle de Mohr associé à la rotation q de la facette n dans le plan MXY en prenant comme repère de référence le repère principal MXY.
Les composantes des contraintes sur les différentes facettes appartiennent toujours à ce plan : les contraintes sont alors dites planes.
2-Expression des composantes normales et tangentielles du vecteur contrainte en fonction de q:
Prenons comme repère initial les axes principaux MX et M Y
Considérons une facette n, inclinée de q par rapport à MX.( La facette en M est représentée par un trait plein).
Soit t le vecteur unitaire, situé dans le plan MXY et faisant un angle de +p/2 avec n. Le repère mobile M,n,t est souvent qualifié de « repère de Mohr »
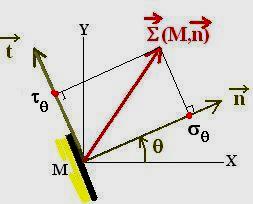
Le vecteur contrainte S s’ecrit dans le repère de Mohr :
![]()
Et dans le repère principal MXY :
![]()
Les composantes des vecteurs unitaires n et t dans le repère principal sont:
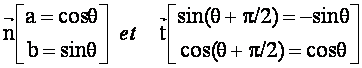
Calculons sq projection du vecteur contrainte sur la normale inclinée de q :
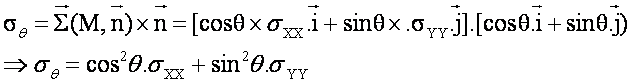

Rappelons quelques formules trigonométriques :
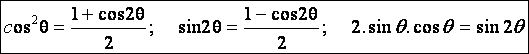
Appliquons cela à la relation précédente, il vient :
![]()
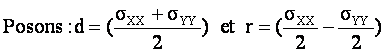
La relation précédente s’écrit alors :
![]()
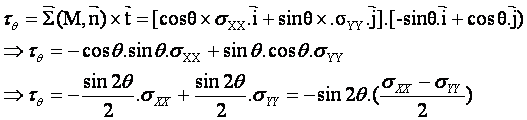
![]()
Dans l’équation (2) l’angle 2q peut être remplacé par -2q. (le cosinus restant identique)
Les relations s’expriment alors en fonction du même angle (-2q)
Les équations (2) et (3) sont les équations paramétriques polaires d’un cercle de centre C(d,0) et de rayon r .
Ainsi pour chaque direction de la facette n nous pouvons associer un point m(sq,tq) sur le cercle représentatif de l’état de contrainte. Lorsque q varie, le point représentatif m décrit le cercle de rayon r et de centre C (d, 0) appelé cercle de Mohr.
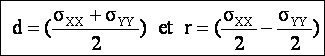
Le signe « moins » devant (2q) indique que la rotation de la normale et la rotation sur le cercle s’effectuent dans des sens opposés.
3-Construction de quelques points représentatifs du cercle pour différentes inclinaisons q de la facette n par rapport à la direction principale MX :
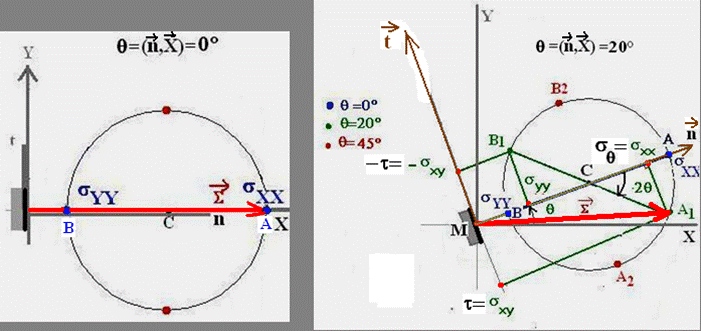
Dans cette partie,les contraintes principales sont notées en rouge pour éviter toute confusion avec les autres contraintes:
*q=0 (normale à la facette confondue avec l’axe MX)
équation (2) : s0=d+r =sXX.( contrainte principale d’axe MX)
équation (3) : t0=0
Le point représentatif sur le cercle est donc le point : m=A (sXX, 0) (point d’intersection du cercle et de l’axe principal MX) .
sXX>0, l’état de contrainte en A est une compression pure
*q=p/2 (normale à la facette confondue avec l’axe principal MY)
équation (2) : sp/2=d-r =sYY. (contrainte principale d’axe MY)
équation (3) : tp/2=0
. Le point représentatif sur le cercle est le point symétrique de A par rapport à C: soit B (sYY, 0). Ce point sur le cercle fait un angle de -2q=-2(p/2)=-p avec MX
syy>0, l’état de contrainte en B est une compression pure
*Considérons maintenant une rotation de la facette de : q=+20°
L’équation (2) devient: s20=d+r. cos(-40°) =sxx.< sXX
équation(3) : t20=r.sin(-40°)=t=sxy
L’angle de -40° sur le cercle est l’angle au centre du cercle soit ACA1.
Le point représentatif sur le cercle est le point A1 (sxx;t)
Si la facette n effectue une rotation d’un angle q , son point représentatif m sur le cercle de Mohr de centre C tourne d’un angle -2q par rapport au point A (s0,t0)
*Rotation de la facette de : q=+(20° +p/2)
équation (2) : s=d+r. cos(-40°-p) = d-r. cos(-40°)=syy>sYY
l'équation (3): t=r.sin(-40°-p)=-t=-sxy
Le point représentatif est B1(syy ,-t) symétrique de A1 par rapport à C.
Aux facettes d’orientation q et q+p/2 correspondent deux points représentatifs A et B symétriques par rapport au centre C du cercle de Mohr.
Remarque : sXX et sYY (contraintes principales) sont les valeurs maxi et mini que peuvent prendre les contraintes normales. Dans une direction non principale, la contrainte normale est toujours comprise entre ces deux extrêmes
*Le point A2 sur le cercle correspond à une inclinaison de q=45° de la facette (soit –(2).45°=-90° pour le point représentatif A2 sur le cercle).
Le point B2 correspond à une inclinaison de q=45°+90° de la facette.(soit :-90°-180° sur le cercle)
Pour q=45° et q=45°+90°, la valeur absolue de la composante tangentielle de la contrainte (t=sxy) est maximum sur la facette. C’est cette valeur de composante tangentielle qui est le plus souvent déterminante pour le choix du matériau.
Par contre en ces deux points, la contrainte normale a une valeur médiane entre sa valeur maximum sXX et sa valeur minimale sYY, soit :s=(sXX+sYY)/2
VI Généralisation : état de contrainte d’une facette orientée selon une direction quelconque de l’espace réel: tricercle de Mohr .
1-Rappel du résultat précédent :
A chaque rotation de la facette dans le plan MXY correspond un cercle dans le repère de Mohr (M,s,t ). Chaque point du cercle de coordonnées (s,t) représente un état de contrainte caractéristique de l’angle q entre la normale à la facette et l’axe origine.
Nous pouvons bien entendu tracer un cercle représentatif pour chaque direction principale MX, MY et MZ. D’où l’appellation de « tricercle » la construction que nous souhaitons réaliser maintenant.
Par soucis de simplicité nous choisirons de représenter les 3 cercles dans un même plan (le »plan de Mohr »)
Soient sXX,sYY,sZZ les trois contraintes principales correspondant aux trois axes principaux.
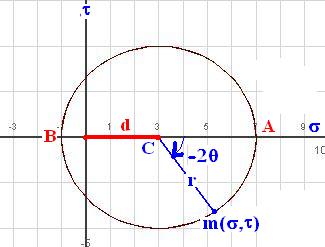
Nous choisirons pour la construction :
![]()
2-Construction du tricercle :
Considérons 3 rotations successives de la normale de 0 à p/2 réalisées dans les 3 plans principaux MXY, MYZ, puis MZY:
-en partant de l’axe MX, la direction normale passe de MX à MY et le point représentatif de A(sXX,0) à B( sYY,0) sur le demi-cercle (C1).
-en partant de l’axe MY, la direction normale passe de MY à MZ et le point représentatif de B(sYY,0) à C(sZZ,0) sur un autre demi-cercle (C2) que nous choisissons de tracer dans le même plan (le « plan de Mohr »)
-enfin, en partant de l’axe MZ, la normale passe de MZ à MX et le point représentatif de C(sZZ,0) à A(sXX,0) sur un troisième demi-cercle (C3)de diamètre sZZ,sXX .
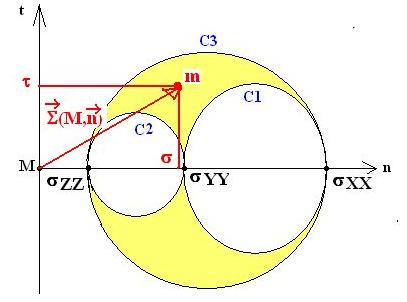
3-Point représentatif des contraintes rencontrées sur des facettes de l’espace réel en M :
Si n possède 3 composantes non nulles dans l’espace MXYZ
On montre que les points représentatifs de l’état de contrainte sont situés au-dessus de C1 et C2 et en dessous ce C3 soit dans la zone orangée ci-dessus. Les cercles représentent les positions limites lorsque la normale reste dans un plan.
C1 si n appartient au plan MXY
C2 si n appartient au plan MYZ
C3 si n appartient au plan MXZ

