TRACTION   

 

Une poutre droite est sollicitée en traction  chaque fois que les actions aux extrémités (A et B) se réduisent à 2 forces égales et opposées qui tendent  à l’allonger. 

Dans le cas où les forces sont orientées l’une vers l’autre, la poutre est sollicitée en compression.

Lors d’une compression il peut y avoir risque de flambage et déversement de la poutre. Le flambage fera l’objet d’une leçon particulière.

Poutre droite sollicitée en traction ou en compression.

(Les directions des forces sont supposées confondues avec l’axe x )

 

Exemple : le câble AC de la structure suivante (potence de manutention) est soumis à 2 actions égales et opposées   

 

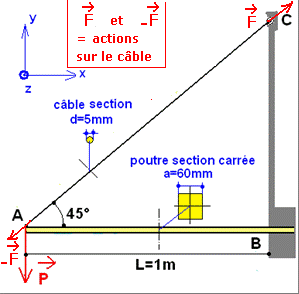
Le câble est soumis à 2 forces opposées d’intensité  F= 2890N de direction AC.

C’est l’essai le plus courant.

Il consiste à exercer 2 forces égales et opposées sur une éprouvette de forme et dimensions normalisées, représentée ci-contre.

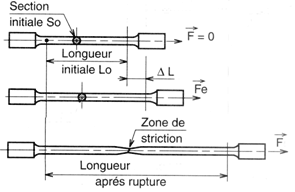
On notera :

DL=allongement (mm)

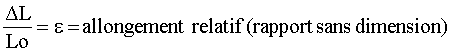
On applique une faible force, on mesure l’allongement, puis on supprime la force. On recommence avec une force un peu plus importante, et ainsi de suite jusqu’à rupture de l’éprouvette.

On obtient la courbe allongement/force qui met en évidence plusieurs zones 

 

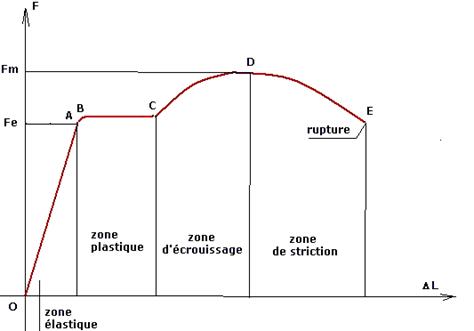
Nous pouvons décomposer le graphe en 3 parties :

1- zone des déformations élastiques F<Fe : droite OA

Dans cette zone l’allongement est proportionnel à la force de traction exercée.

Lorsque la force cesse, l’éprouvette reprend sa forme initiale. Celle-ci se comporte comme un ressort. .La relation entre F et DL est linéaire, soit :

En divisant cette expression par la section S de l’éprouvette, on obtient la force par unité de section ou contrainte de traction (notée s), soit

 

 

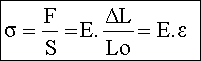
Cette relation linéaire s’appelle LOI DE HOOKE.

 

Voir ci-dessous le tableau donnant les valeurs de E pour différents matériaux

2- zone des déformations permanentes Fe< F <Fm

courbe ABC :

La force limite élastique étant atteinte l’éprouvette continue de s’allonger sans que la force soit nécessairement  augmentée. L’éprouvette restera déformée si la force est annulée. C’est une déformation dite plastique. Les matériaux comme l’acier qui ont se comportement sont dits ductiles. L’acier peut se plier sans se rompre comme beaucoup de métaux.Cette propriété permet de créer des formes particulières comme en chaudronnerie par exemple.

courbe CD :

Le matériau subit un changement de structure qui accroît sa résistance.  C’est l’écrouissage.

3- Zone F>Fm, rupture progressive de l’éprouvette

L’éprouvette subit une diminution brutale de sa section avec étranglement ou  striction ce qui

réduit la force de traction alors que l’allongement augmente brutalement

La rupture est amorcée, elle survient au point E.  

Sa section est :

Nous supposons que la force F est répartie uniformément sur toute la section (*) du câble.

Dans ce cas la contrainte est identique en tous les points de celle-ci et vaut :

 

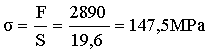
Unités : F en N ; Sen mm²  et s en MPa

(*) cette condition n’est pas toujours réalisée en particulier à proximité d’un changement brutal de section.

 

Utilisons les données sur le matériau utilisé pour le câble.

Il est réalisé en acier de limite élastique Re=300MPa et de résistance à la rupture :

 Rr =500MPa

Pour vérifier la bonne résistance du câble nous devons comparer s à Re qui est la limite de résistance élastique du matériau utilisé Re exprimée aussi en MPa.

Ici Re =300MPa donc s<Re, la déformation du câble reste dans le domaine élastique.

 

Pour tenir compte des imperfections du matériau et la présence de surcharge éventuelle dépassant la valeur théorique nous appliquerons un coefficient de sécurité s=1,5 :

On définit alors :La résistance pratique élastique Rpe

 

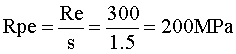
On a donc : s<Rpe , le diamètre d choisi pour le câble est donc validé

ATTENTION :

Toute variation brusque de section dans une pièce sollicitée en traction amplifie la valeur de la contrainte à proximité des variations. On parle de concentration de contrainte.

1-allongement :

A partir de la loi de Hooke, déterminons l’allongement du câble :

 

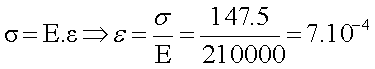
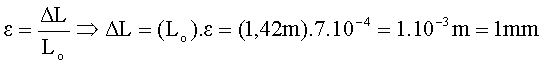
2-Contraction latérale –coefficient de Poisson :

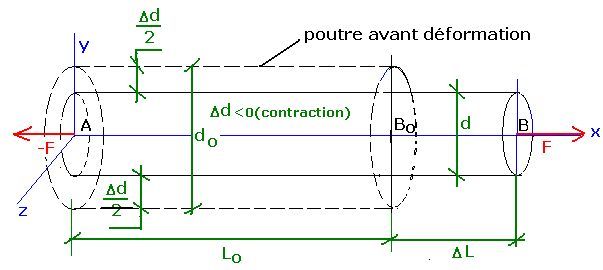
Le câble se contracte de Dd dans la direction perpendiculaire à l’allongement Dl

Le coefficient de Poisson n est le rapport contraction relative/allongement relatif

 

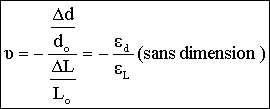
(Le signe – résulte de Dd<0)

Pour le câble en acier, nous prendrons n=0,3

Il en résulte une contraction latérale du câble de :

(soit environ 1 micromètre !)

 

Lors d’un changement brutal de section (épaulement, gorge, trou), la contrainte n’est plus uniforme, elle est maximum à proximité de l’épaulement, de la gorge et sur les bords du trou. Pour tenir compte de cette « concentration » locale  de contrainte, on pondère la valeur de la contrainte calculée précédemment  d’un coefficient Kt.

La valeur à prendre en compte est :

 

s_o est appelée « contrainte nominale » c’est la valeur de la contrainte uniforme qui s’exerce sur la section la plus petite de la pièce à proximité du changement de section. 

La valeur de Kt dépend de la forme apportée à la variation de section.

Exemple : cas d’un arbre avec épaulement sollicité en traction par une force d’intensité F

Le schéma ci-dessous indique que la contrainte n’est pas uniforme au niveau de l’épaulement, elle est maximum  à la périphérie de la section.

 

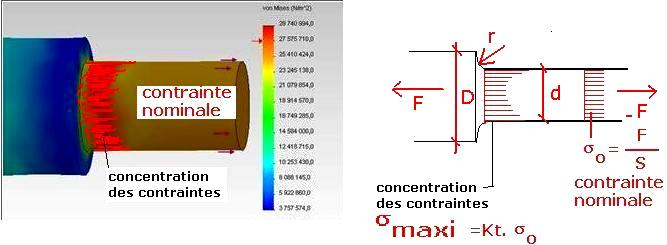
Données :

L’arbre est soumis à un effort normal de F de 30000N,

D=30mm ; d=20mm

Contrainte nominale : 

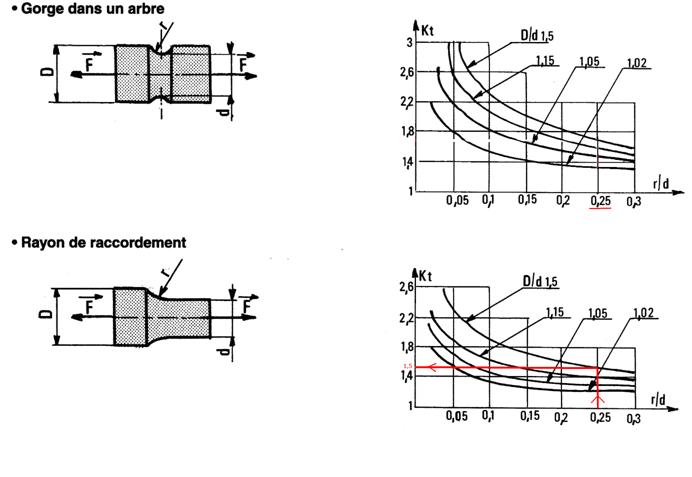
On a D/d=30/20=1,5   et r/d=5/20=0,25

Se servir du 2^ème abaque ci-dessous pour évaluer Kt  (trait rouge) ou de la feuille de calcul Excel proposée dans la médiathèque:

On peut lire :Kt=1,5, d’où la contrainte maxi : s_Maxi=1,5x95,5=143MPa

 

Remarque : Observons l’image colorée ci-dessus. Supposons que la contrainte normale uniforme (représentée par la couleur marron) dans l’arbre de diamètre d à droite soit proche de la limite élastique Re. Une augmentation brutale du diamètre à une extrémité de l’arbre (à gauche) pourrait rendre la contrainte trop forte au niveau de l’épaulement (couleur rouge) alors qu’elle serait plus faible bien entendu au de là de celui-ci avec un diamètre D (couleur bleue)!  L’épaulement peut donc affaiblir notablement la résistance de la pièce.

 

Valeur de Kt pour un arbre avec gorge ou épaulement  :

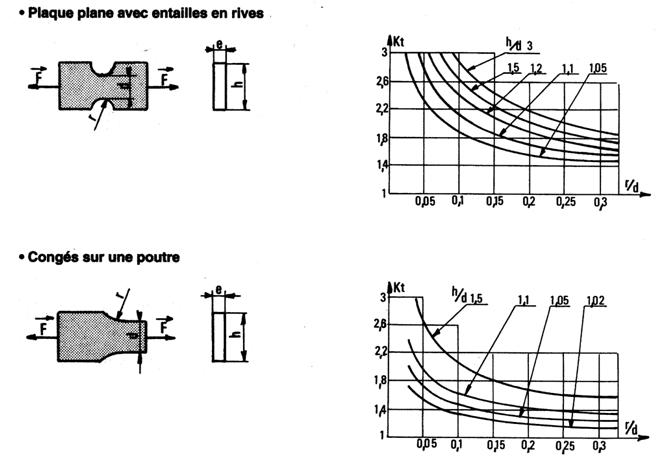
Valeur de Kt pour un fer plat avec entaille ou congé

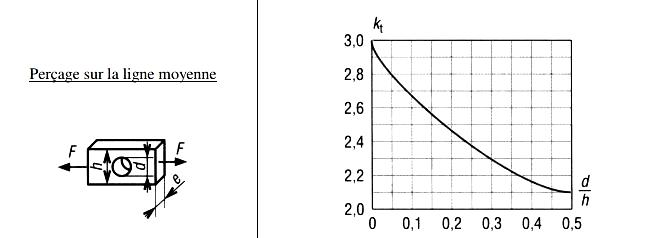
Valeur de Kt pour un fer plat percé dans l’axe

 

On pourra aussi évaluer Kt en utilisant le tableur Excel (voir documents suivants proposés dans la médiathèque)

E = module d’élasticité longitudinal en MPa

r = masse volumique en kg/m3

Re = résistance élastique en MPa

Quelques exemples :

 Exercice d’application 

Un plat de largeur h=60mm et d’épaisseur e=10mm comporte un rétrécissement de rayon r=10mm et un trou de diamètre d=8mm.

Si la force de traction est F=1000daN, déterminer les contraintes maximales au niveau du rétrécissement (s_r) et au niveau du trou (s_t)

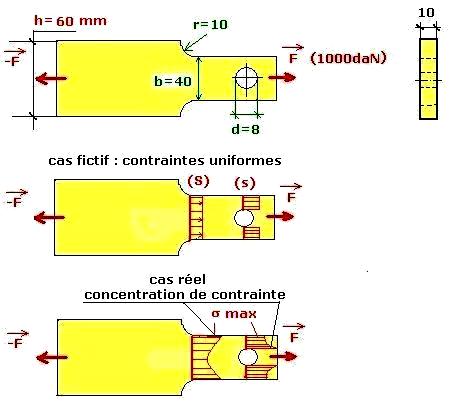
Contrainte nominale (en supposant la contrainte uniforme) dans la plus petite section (S) 

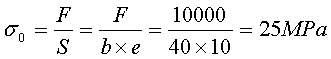
Contrainte maximale s_r au niveau du rétrécissement :

Détermination de  Kt coefficient de concentration de contrainte.

 

a-Utilisation de l’abaque « congé sur une poutre » proposé ci-dessus :

 

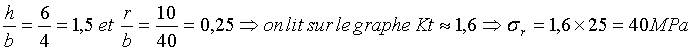
b-Utilisation du tableur Excel :

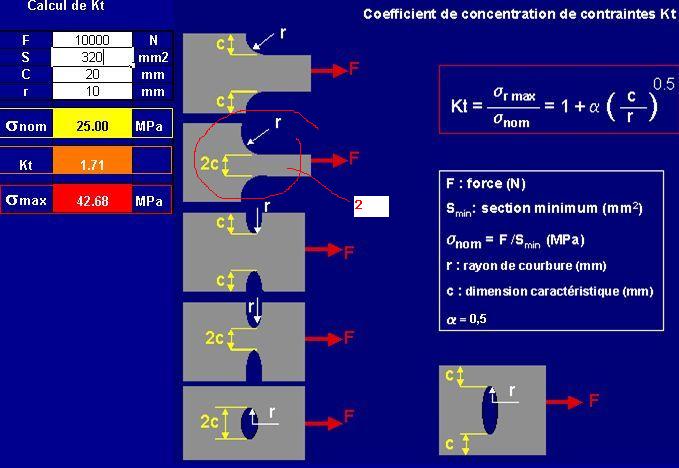
Repérons les dessins correspondant à la situation étudiée : fer plat avec rétrécissement soumis à un effort normal: Les 2 premiers dessins peuvent à priori convenir.

Parmi ces derniers il faut choisir celui qui donne la plus grande valeur à C (et donc à Kt )

Sur le dessin n°2, 2C=40mm soit C=20mm alors que sur le premier dessin C=(h-b)/2=10mm

On obtient Kt=1,71 et

s_max=s_r=42,7MPa (voir ci-dessous)

(Cette valeur est comparable avec celle de l’abaque)

Cette contrainte maxi affecte les bordures du fer plat à proximité du congé.de raccordement des 2 sections

Source :http://formatechtv.free.fr/

Contrainte maximale sur les bords du trou :

Détermination sur l’abaque « perçage sur la ligne moyenne » :

d/h=40/8=0,2  alors Kt=2,45

Détermination de Kt avec le tableur :

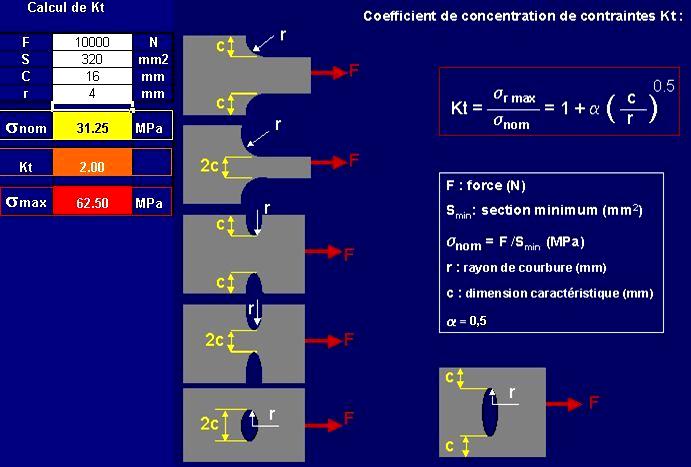
Nous utilisons le 6éme dessin : pièce soumise en traction avec perçage 

Données à introduire dans le tableur : C=(40-8)/2=16mm  et  r=8/2=4mm

La valeur Kt=2,0  représente une différence notable avec l’abaque.

(l’utilisation du tableur semble mal adaptée pour cet exemple)

Résultat (avec l’abaque)

Contrainte nominale dans la plus petite section s :

:  

Cette contrainte maxi affecte le bord du trou

 

Source :http://formatechtv.free.fr/