Etude géométrique d’une section de cornière inégale

 L’objectif de ce document est d’appliquer toutes les connaissances relatives aux sections droites

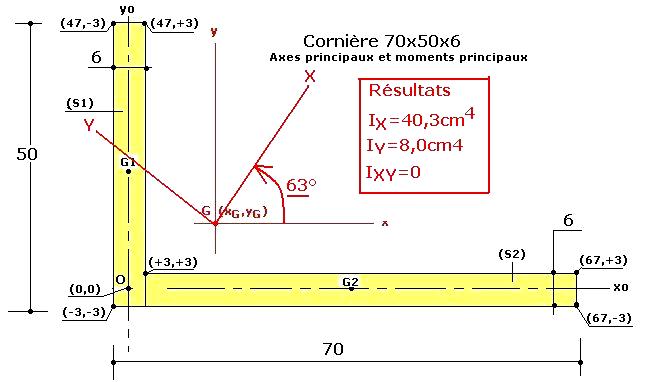
La section est de 70x50x6 .Toutes les cotes sont en mm.

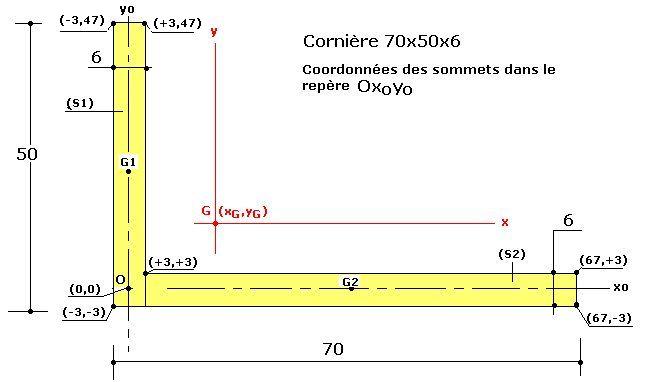
1-Détermination des coordonnées du centre de gravité dans le repère Ox_oy_o:

Le choix de ce repère permet de simplifier les calculs au maximum

La section totale S est partagée en deux rectangles S₁ et S₂ de centre de gravité respectifs G₁ et G₂.Les arrondis aux extrémités de la section sont négligés.

S₁=50x6=300mm², S₂=64x6=384mm², S=S₁+S₂=684mm².

G est barycentre de G₁(S₁) et G₂(S₂), soit :

Egalité projeté sur Gx : 

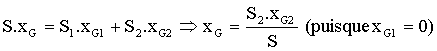
Egalité projeté sur Gy :

x_G2=3+(70-6)/2=3+32=35mm ; y_G1=50/2 -3 =22mm

Application numérique :

 

2-Calculs des moments quadratiques de la section S par rapport aux 2 axes Gx et Gy :

Le schéma précédent est complété des distances (en vert) entre les axes de chaque rectangle et les axes du repère Gxy pour l’application du théorème de Huyghens. 

 

 

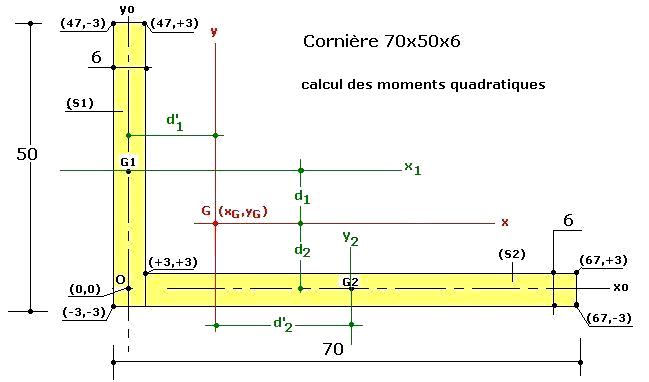
Moment quadratique de S par rapport à Gx :

I_Gx=I_Gx(S₁) +I_Gx(S₂)

(Théorème de Huyghens G₁x₁//Gx) :I_Gx(S₁)=I_G1x1(S₁)+S₁.d₁².

d₁=OG₁-y_G=22-9,65=12,35mm, soit numériquement:

 

(Théorème de Huyghens G₂x_o//Gx) I_Gx(S₂)=I_G2xo(S₂)+S₂.d₂².

Avec d₂=y_G=9,65mm

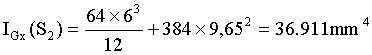
Soit: I_Gx=108.257+36.911=145.168mm⁴.=14,5cm⁴.

Moment quadratique de S par rapport à Gy:

I_Gy=I_Gy(S₁) +I_Gy(S₂)

(Théorème de Huyghens G₁y_o//Gy):I_Gy(S₁)=I_G1yo(S₁)+S₁.d’₁².

d’₁=x_G=19,65mm

 

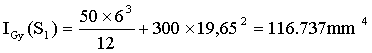
(Théorème de Huyghens G₂y₂//Gy):I_Gy(S2)=I_G2y2(S2)+S₂.d’₂².

d’₂=OG₂-x_G=35-19,65=15,35mm

 

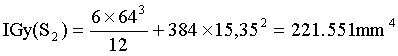
IG_y=116.737+221.551=338.288mm⁴=33,83cm⁴

3-Axes principaux et moments quadratiques principaux de S :

3-1-calcul du  moment produit Ixy

Ixy(S)=Ixy(S₁)+Ixy(S₂)

I_xy(S)=Ix_oy_o(S₁)+S₁.d’₁.d₁+Ix_oy_o(S₂)+S₂.d’₂.d₂.

Les moments produits  notés en rouge sont nuls car l’un des 2 axes est axe de symétrie de la section. D’autre part d’₁ et d₂ sont négatifs (voir fig ci-dessus)

 

3-2 Utilisons le tableur pour évaluer les moments principaux.

Les 3 données : I_Gx=14,5cm⁴, I_Gy=33,83cm⁴, Ixy=-12,97cm⁴ suffisent

Lien vers le tableur de calcul des moments principaux