Moment quadratique d’une surface .Importance de cette notion définition et exemples de calcul (html)

Moment quadratique (ou moment d’inertie) d’une section

Théorème de Huyghens

Sources : http://fr.wikipedia.org/wiki/Moment_quadratique

liengeniecivil.wifeo.com/documents/Chap-8-Caractrisques-gomtriques-des-sections-V2001.pdf

I-Introduction :

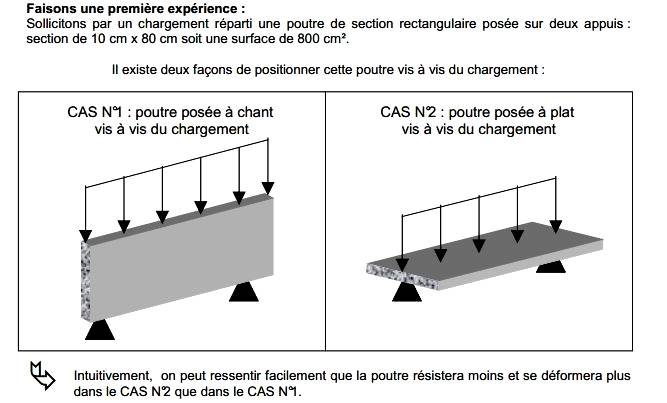
La grandeur qui prend en compte cette rigidité est le moment d’inertie Iz (ou moment quadratique) de la section par rapport à l’axe de flexion de la poutre.

Le moment quadratique est maximum dans le cas n°1 car la matière s’éloigne le plus de l’axe longitudinal de la poutre, il est minimum dans le cas n°2.

II-Définition générale :

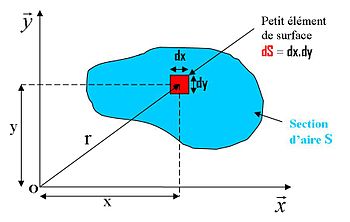
Considérons dans une section d’aire totale S un petit élément de surface dS situé à distance y de l’axe x et à distance x de l’axe y.

Le moment quadratique élémentaire de l’élément dS par rapport à l’axe Ox est égal au produit dS par sa distance au carré à l’axe Ox , soit :

dIx= y². dS

Pour obtenir le moment quadratique de toute la surface S par rapport à Ox, il faut réaliser une sommation de tous les moments élémentaires dIx, c'est-à-dire l’intégrale de l’expression précédente étendue à toute la surface .

Ce qui s’écrit :

$I_x = \int_{S}y^2\, \mathrm ds = \iint_{S}y^2\, \mathrm dx\mathrm dy$

De même le moment quadratique de la section par rapport à l’axe Oy :

$I_y= \int_{S}x^2\, \mathrm ds = \iint_{S}x^2\, \mathrm dx\mathrm dy$

Enfin le moment quadratique polaire de S par rapport au point :

$I_O= \int_{S}r^2\, \mathrm ds = \iint_{S}r^2\, \mathrm dx\mathrm dy$

Comme :

Remarque: il découle de ces définitions que plus les éléments de la section sont situés loin de l'axe, plus le moment quadratique sera important.

Ce dernier est en effet proportionnel au carré de la distance de la section à l’axe

L’unité SI du moment quadratique ou polaire est le m⁴. On utilise aussi cm⁴ ou mm⁴.

III-Application de la définition :

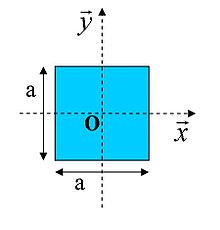
Section carrée

Pour une section carrée de côté centrée en :

Moment quadratique par rapport à Ox :

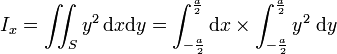
$I_x= \iint_{S}y^2\, \mathrm dx\mathrm dy = \int_{-\frac {a}{2}}^{\frac {a}{2}} \mathrm dx \times \int_{-\frac {a}{2}}^{\frac {a}{2}} y^2 \;\mathrm dy$
$= \left[\frac {a}{2}-\left ( - \frac{a}{2} \right ) \right] \cdot \frac {1}{3} \cdot \left[ \left(\frac {a}{2}\right) ^3 - \left ( - \frac{a}{2} \right ) ^3 \right] = \frac {1}{3} \cdot a \cdot \left ( \frac {a^3}{8} + \frac {a^3}{8} \right )$
$= \frac {a^4}{12}$

Moment quadratique par rapport à Oy : à cause de la symétrie de cette section, on a :

$I_y= \frac {a^4}{12}$

Moment quadratique par rapport au point 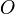: En utilisant le fait que

on a donc :

$I_O= \frac {a^4}{6}$

IV-Formules pour les sections usuelles

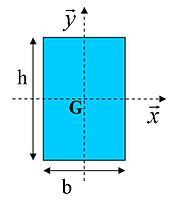
Section rectangulaire

$I_x= \frac {b \cdot h^3}{12}$

$I_y= \frac {h \cdot b^3}{12}$

$I_G= \frac {b \cdot h}{12} \cdot (b^2+h^2)$

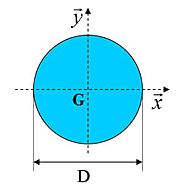
Section circulaire

$I_x= \frac {\pi \cdot D^4}{64}$

$I_y= \frac {\pi \cdot D^4}{64}$

$I_G= \frac {\pi \cdot D^4}{32}$

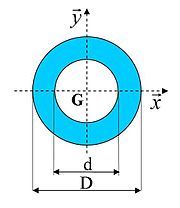
Section annulaire

Il s'agit simplement de soustraire le moment quadratique du disque intérieur à celui du disque extérieur.

$I_x= \frac {\pi \cdot (D^4-d^4)}{64}$

$I_y= \frac {\pi \cdot (D^4-d^4)}{64}$

$I_G= \frac {\pi \cdot (D^4-d^4)}{32}$

V-Théorème de HUYGHENS :

Soit à déterminer le moment quadratique de la section ci-dessous par rapport à l’axe D parallèle à l’axe Gx .

Enoncé du théorème : le moment quadratique d’une section S par rapport à l’ axe D est égal au moment quadratique de S par rapport à l’axe passant par son centre de gravité G

auquel on ajoute le moment quadratique de la section S (supposée concentrée au point G) par rapport à D. (ce terme ajouté s’appelle souvent « transport de Huyghens »)

Modifié le: Thursday 21 July 2016, 09:28