Moment statique d’une section -Centre de gravité définition et méthode de détermination de G (html)
Résumé de section
FPI
NIVEAU : 1ère, 2ème, 3ème Année BEP
BACC PRO
SECTEUR : INDUSTRIEL
FILIERE : STRUCTURES METALLIQUES
OPTION : METAUX EN FEUILLES
Référence sous module : SMF/T/08-06
|
Intitulé du sous module : AXES PRINCIPAUX D’UNE SECTION SIMPLE Objectif intermédiaire : A l’issue du sous module de formation, l’apprenant doit être capable de : CONNAITRE la définition des axes principaux d’une section simple. |
Réf. : SMF/T/08 - 06 |
||
|
INDEXATION |
UNITES DE FORMATION |
DUREE |
|
|
UF/T/08 – 06 – 01 UF/T/08 – 06 – 02 UF/T/08 – 06 – 03 |
Moment statique Moment quadratique Moment quadratique polaire |
|
|
TOTAL |
10 h |
||
Remarque: toutes ces notions sont développées dans le document ci-dessous et les suivants.
Détermination du centre de gravité d’une section
I- MOMENT STATIQUE d’une section :
En résistance des matériaux, le moment statique est une grandeur physique qui caractérise la géométrie d'une section et se définit par rapport à un axe. Il intervient notamment comme ci-dessous dans le calcul de la position du centre de gravité mais aussi des contraintes de cisaillement (lors d’une flexion). Il a la dimension d'un volume (m3 dans le système international d'unités S.I).
Le moment statique d'une section de densité homogène, par rapport à un axe ![]() (noté QD ) est égal au produit de l'aire S de cette section par la distance d de son centre de gravité G à l'axe.
(noté QD ) est égal au produit de l'aire S de cette section par la distance d de son centre de gravité G à l'axe.
QD= S.d (unité SI=mxm2=m3)
Une conséquence importante de cette définition est que le moment statique d'une section de densité homogène, par rapport à un axe passant par son centre de gravité, est nul.
II- DEFINITIONS : centre de gravité et centre de masse
Considérons un solide de masse m. Soit à déterminer la position de son centre de gravité G.
Soient XG , YG, ZG les coordonnées de G relatives à un repère rectangulaire Oxyz.
Décomposons le solide en solides élémentaires de masse respective m1 ,m2 m3…et de centre de gravité respectifs : G1, G2, G3 etc…
Par définition G centre de gravité est le barycentre des poids des solides élémentaires
Ce qui s’écrit en mathématiques:
![]()
Le champ de pesanteur étant uniforme pour l’ensemble du solide, la relation peut être simplifiée en éliminant g :
![]()
Ce qui revient à dire que G est aussi le barycentre des masses.
C’est pourquoi G dans ce cas s’appelle aussi : centre de masse.
Remarque : la distinction entre centre de gravité et centre de masse est nécessaire lorsque le solide est plongé dans un champ de pesanteur qui n’est pas uniforme. C’est le cas pour un objet de hauteur très importante car comme on le sait g diminue avec la hauteur. Par exemple pour un édifice de 300m de haut les deux points peuvent être éloignés de quelques mm ! Dans notre étude les deux points sont évidemment confondus et il n’y a donc pas lieu de faire une distinction entre centre de masse et centre de gravité.
III- Formules générales donnant la position du centre de gravité d’une section plane d’aire S d’une poutre :
La section peut être décomposée en éléments de forme géométrique simple (comme ici des rectangles) de section S1, S2, S3 dont les centres de gravité G1, G2, G3…sont connus.
Dans la formule précédente les masses sont remplacées par les sections:
![]()
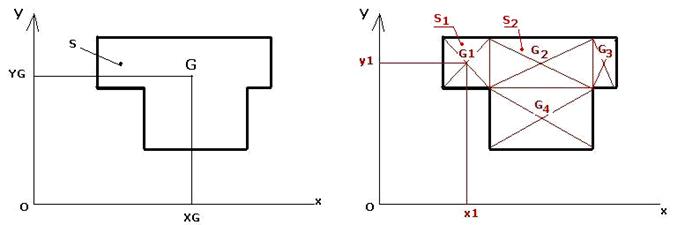
G centre de gravité est le barycentre des différents points G1, G2, G3 …affectés des coefficients S2, S2, S3….
En appelant XG et YG les composantes du vecteur OG, Xi et Yi les composantes des différents vecteurs OG1, OG2…etc, on obtient les relations algébriques.
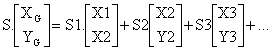
soit
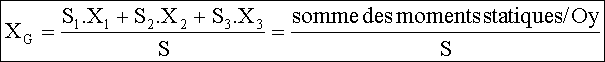
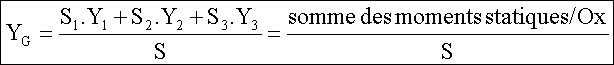
Attention certaines sections peuvent aussi résulter d’une soustraction d’éléments simples comme nous le verrons dans l’exemple qui suit. C’est pourquoi le terme au numérateur peut être une somme algébrique suivant le choix des éléments..
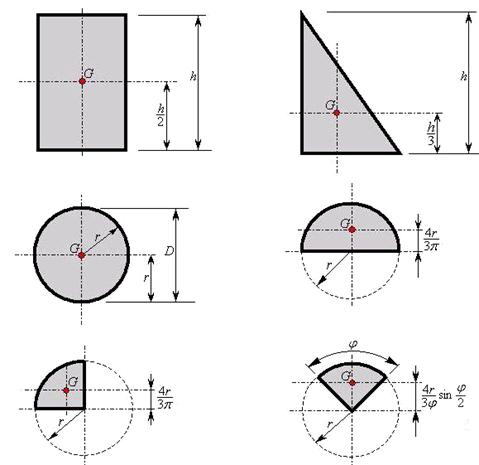
IV- Position du centre de gravité de quelques sections simples :
Source :http://math.15873.pagespro-orange.fr/page9.htm
IV- Méthode de détermination du centre de gravité d’une section composée:
Source :http://math.15873.pagespro-orange.fr/page9.htm
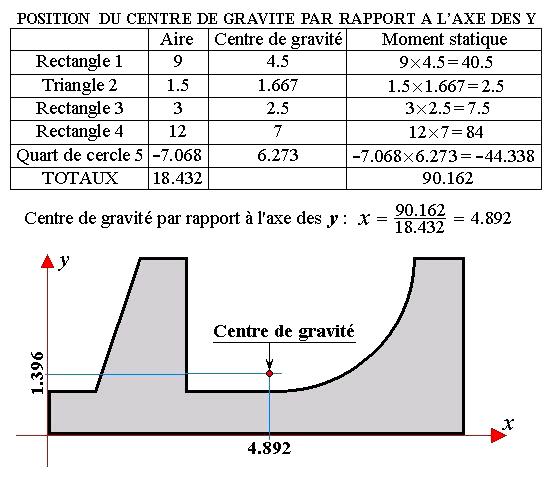
Soit à déterminer le centre de gravité de la section ci-dessous :
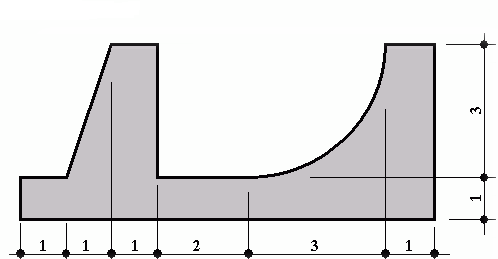
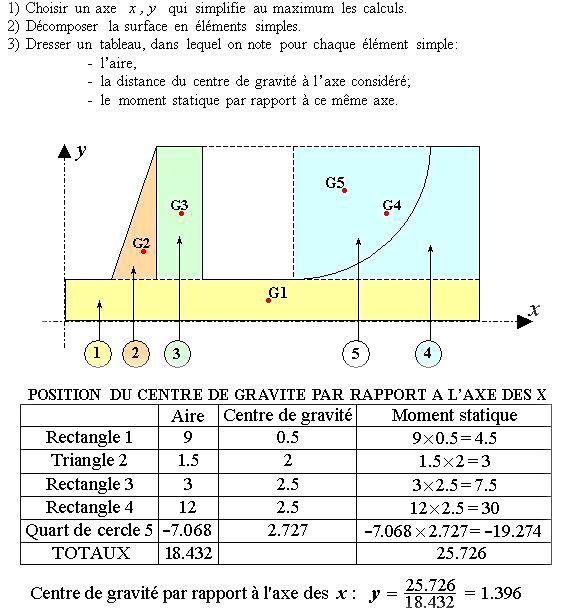
Remarque : L’aire de la section S est ici égal à S1+S2+S3+S4-S5. Le moment statique de l’élément 5 doit donc être retranché.
Les coordonnées du centre de gravité x et y sont donc égaux à la somme algébrique des moments statiques des sections élémentaires par rapport aux axes Ox et Oy divisée par l’aire totale de la section S