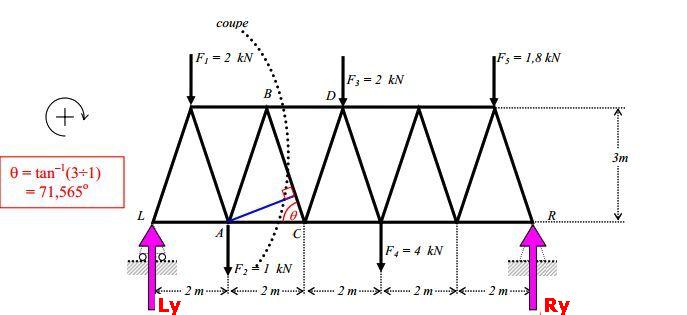
Exercice sur la méthode des sections

Sous module traité UF/05/04/04: Systèmes triangulés, Méthode de Ritter (ou des sections)

Source : http://mlamontagne.ep.profweb.qc.ca/solutions_rdm.htm

 Déterminer  les efforts dans les barres AC, BD et BC de la structure treillis représentée ci-dessous. On précisera s’il s’agit d’une  traction ou d’une compression.

Convention de signe pour les moments: une force qui tend à faire tourner la structure autour d’un point dans le sens positif arbitraire indiqué possède un moment positif.

Recherche de la réaction L_y 

Écrivons que la somme des moments de toutes les forces par rapport à R est nulle :

(notation utilisée : en vert la valeur de la force, en rouge le bras de levier, le signe dépend de la convention)

L_yx10 – 2x9 - 1x8 - 2x5 - 4x4 - 1.8x1 + Ryx0=0 => L_y=5,38kN

Recherche des efforts dans les barres :

Notation : l’effort dans une barre est symboliquement donné par l’écriture du segment précédé d’un signe 

Méthode : on réalise une coupure fictive de la structure traversant les barres inconnues. Les efforts recherchés deviennent des  forces extérieures appliquées aux nœuds A et B qui équilibrent la partie gauche de la coupure. Le sens d’orientation des forces sur le dessin est arbitraire, c’est le calcul qui déterminera le sens réel.

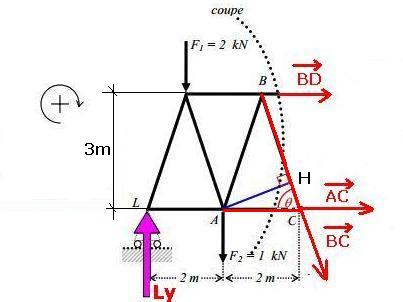
Détermination de l’effort (noté « AC ») dans la barre AC :

5.38x3 - 2x2 - 1x1 - ACx3 - BCx0 - BDx0 =0 => AC=+3,71kN

Le sens de la force est celui indiqué sur la figure, elle tire donc sur le nœud A. La barre est donc tendue.

Effort dans BD :

5,38x4 - 2x3 - 1x2 - ACx0 - BCx0 + BDx3 =0 => BD=-4,5kN

Le sens de la force est le sens contraire de celui indiqué, elle agit de D vers B, elle pousse sur le nœud B. La barre est comprimée.

Effort dans BC :

5,38x2 - 2x1 + ACx0 + BDx3 + BCxAH = 0

AH=AC.sinq =2.sin(71,56°)=2.0,949=1.9m

5,38x2-2x1+ACx0 +(-4,5)x3+BC x(1,9)=0

Le sens de la force est celui indiqué sur la figure, elle agit de B vers C, elle tire sur le nœud B. La barre BC est donc tendue.