Ce document a été conçu par l’association ACCESMAD a destination des élèves  de  l’enseignement   technique  de  Madagascar. Il   propose une méthode pédagogique  d’assimilation des contenus du texte des programmes intitulé:

REPOBLIKAN’I MADAGASIKARA

Module de formation : mécanique et résistance des matériaux

LES SYSTEMES TRIANGULES PLANS

Ref :SMF/05/04

Objectif général intermédiaire : A l’issue du sous-module, l’apprenant sera capable de DETERMINER la nature et l’intensité des efforts dans les barres d’un système triangulé en vue  de leur prédimensionnement

Exercice proposé : étude d’une structure treillis

I- Objectifs de l’exercice :  

- vérifier si la structure est bien isostatique,

- utiliser la méthode graphique de Crémona pour évaluer les efforts dans la structure,

- utiliser une méthode énergétique pour évaluer un déplacement.

II- Enoncé :

On considère la poutre suivante :

 

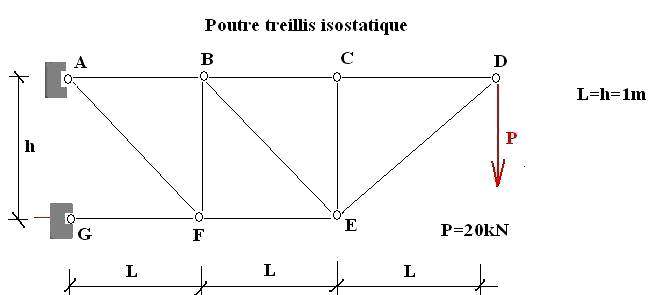
On demande d’effectuer les recherches suivantes:

1- vérifier que la structure est isostatique,

2-évaluer les réactions aux appuis,

3-déterminer les efforts dans chacune des barres par une méthode graphique,

4-sachant que la section des barres est A=706.9mm², évaluer les déplacements vertical V_D et horizontal H_D  au point D. On utilisera une méthode énergétique. On vérifiera les résultats avec le logiciel RDM6.

III-Résolution

1- La structure est isostatique si le nombre de forces inconnues (Ninc) dans la structure et à l’extérieur de celle-ci est égal au nombre d’équations d’équilibre (Neq)

1-a  Nombre de Barres (B) et nombre de nœuds (N) :

Un treillis est une structure triangulée articulée sur des nœuds. En conséquence les barres ne reçoivent que des efforts normaux. Les nœuds constituent les sommets des triangles .Un nœud se trouve donc à l’intersection d’au moins 2 barres.

Le point G ne recevant qu’une barre n’est pas un nœud. La barre GF n’appartient pas à un triangle formé de 3 barres ; elle  ne fait que transmettre la réaction en G  sur le nœud F.

La poutre treillis est donc limitée au domaine A, B, C, D, E, F, A, elle possède 6 nœuds et 9 barres.

B=9 et N=6

1-b-Nombre de forces  inconnues :

L’effort normal dans chaque barre constitue une inconnue. L’ensemble des 9 barres apportent donc B= 9 inconnues.

Les actions des liaisons extérieures  aux points A et G sont également des inconnues.

La réaction (R_G) en G est l’opposée de l’effort normal apporté par la barre GF. Celle-ci possède une composante  horizontale, soit X_G .

La réaction (R_A) en A s’oppose aux efforts normaux apportés par les deux barres AB et AF, elle possède deux inconnues X_A et Y_A . Les actions de liaison représentent donc 3 inconnues.

Le nombre total d’inconnues est donc égal à :

Ninc=B+3=12

 

1-c-Nombre d’équations d’équilibre:

Chaque nœud est en équilibre. La somme des projections (algébriques) des forces sur x et sur y doivent être nulle ce qui entraine deux équations d’équilibre par nœud.

Neq=2.N=12

La relation « B+3=2N » ou « B=2N-3 » est vérifiée ; elle est souvent retenue pour caractériser l’isostaticité.

2-Détermination des réactions aux appuis :

Commençons par choisir un repère rectangulaire Gxy (voir fig). Représentons les projections des forces agissant en A et G. La barres FG est articulée en G et F, elle ne transmet qu’un effort normal de direction horizontale à l’appui G ,la composante verticale YG est donc nulle. Attention ici le sens des forces est celui des axes du repère , il ne correspond pas forcément au sens réel. C’est le signe après calcul qui le déterminera.

 

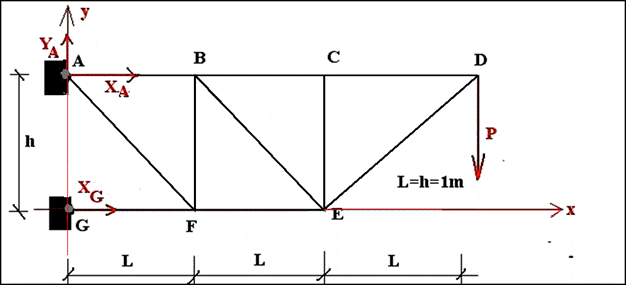
Le  système étant en équilibre, le principe fondamental de la statique(P.F.S) permet d'écrire les 2 conditions:

a- La somme des forces extérieures agissant sur la structure doit être nulle:

 

Les forces extérieures sont : la charge d’exploitation P et les réactions aux appuis en A et G

Soit, en projetant sur Ox (les projections étant des grandeurs algébriques):

Puis sur Oy:

b-La somme des moments des forces extérieures en un point doit être nulle: C’est le point G qui est choisi pour évaluer les moments :

L’équation des moments en G se résume à :

3-Efforts dans les barres (utilisation de la méthode graphique de Crémona):

3-1 Principe de la construction 

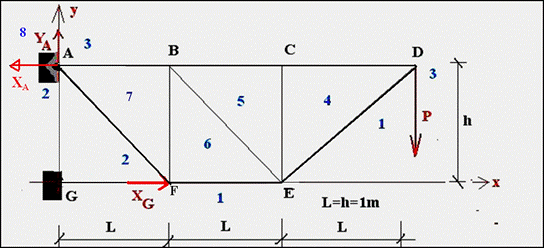
 La structure est partagée en domaines numérotés (ici de 1 à 8).Ces domaines sont délimités par les barres et les forces extérieures à la structure.

Par exemple, la force P partage le plan en 2 domaines 3 et 1. La force P est représentée par le segment 3-1 sur le graphique.

La structure est en équilibre, cela signifie qu'à chaque nœud, la somme des forces est nulle. On trace pour chaque nœud  un polygone en mettant les forces bout à bout. Celui-ci doit se fermer.

Le polygone ne peut être construit que si les efforts dans 2 barres au plus qui convergent vers le nœud sont inconnus.

Il n’est pas possible par exemple de commencer  la construction à partir du nœud E point d’intersection de 4 barres ayant des efforts encore inconnus.

Commençons par l’équilibre du nœud D. Représentons la force P par le segment 3->1.

A partir de l’extrémité (point 1) traçons une parallèle à la barre DE puis à partir de  l’origine (point 3) tracer une parallèle à DC. L’intersection  donne le point 4. Point de fermeture du polygone du nœud D.

 

On tracera ensuite le polygone au nœud C : Celui-ci ne reçoit aucune force extérieure  et reçoit 2 barres de même direction horizontale (CD et CB). Ceci permet d’affirmer que l’effort dans la barre CE est nul (voir plus loin l’explication*). Les points 4 et 5 du Crémona sont donc confondus.

 

Il est possible de passer ensuite à l’équilibre du nœud E qui reçoit les deux barres EB et EF dont les efforts sont encore inconnus. On réalisera l’équilibre des nœuds : B puis F puis A.

 

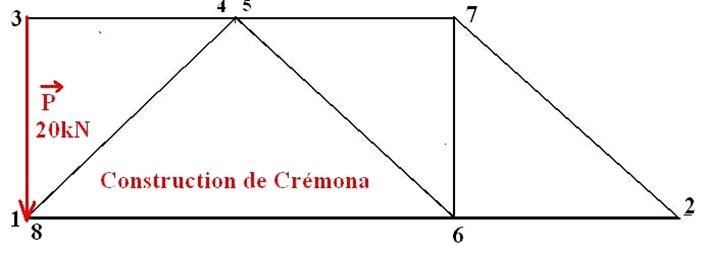
3-2 Exploitation du graphique :

En tournant  autour du nœud dans le sens horaire 3->1->4->3  on déduit le type de sollicitation :

Ainsi 1->4 désigne la force dans la barre DE ; sur le graphique elle agit en diagonale vers le haut, elle « pousse » donc sur le noeud  D, cette barre est donc comprimée.

De même 4->3  représente  la force dans la barre DC ; sur le graphique Crémona  celle-ci  agit de la droite vers la gauche, elle« tire » donc sur le nœud D, cette barre est donc tendue.

Ayant choisi au départ une échelle des forces, la longueur des segments construits permet de déterminer l'intensité des forces.

Regroupons les résultats dans un tableau :

Remarque : La somme vectorielle des forces extérieures P+XG+XA+YA correspond au polygone :

3->1->2->8->3 sur le crémona. Cette somme est nulle puisque la structure treillis dans son ensemble est en équilibre sous l’effet des charges extérieures.  

Efforts évalués par le logiciel RDM6

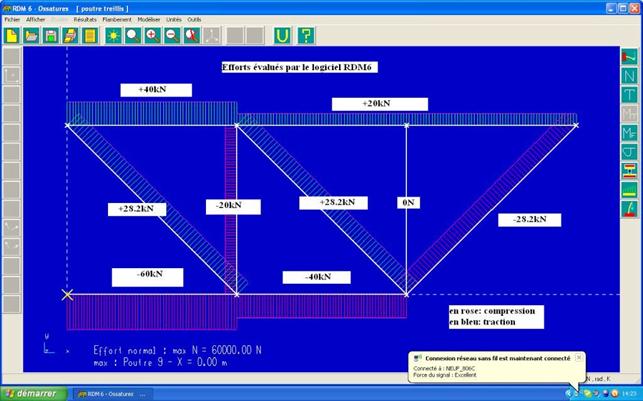
(*) vérifions que l’effort dans le montant CE est nul :

considérons 3 forces s’exerçant sur un même nœud et dont deux ont le même support.

Effectuons la somme vectorielle :

 en plaçant les vecteurs bout à bout comme l’indique la figure ci-dessous.

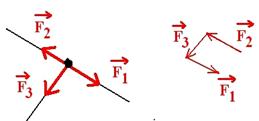
Sachant que les deux forces F₁ et F₂ ont même support, sur le polygone des forces elles sont parallèles. Dans ce cas celui-ci ne peut se fermer .L’équilibre n’est possible que si :

 

Ce résultat est général :

Lorsqu’un nœud ne recevant aucune charge extérieure est le point d’intersection de 3 barres dont deux ont même support, les efforts dans les deux barres de même support sont opposées et l’effort dans la troisième barre est nul.

Les questions suivantes sont traitées pour les lecteurs voulant approfondir leurs connaissances dans le domaine énergétique.

Elles sont considérées hors programme des lycées

4-déplacements  du point D :

4-a : déplacement vertical V_D

Nous allons mettre en œuvre une méthode énergétique pour évaluer ce déplacement

Sous l’effet de la force extérieure P, la structure se déforme élastiquement.

P et V_Dy ayant  même direction

Le travail de cette force élastique est :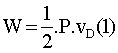      

En l’absence de frottements ce travail est converti en énergie potentielle élastique du système déformé soit U.

Le potentiel s’exprime simplement en fonction des éléments du torseur de cohésion de chaque section M (moment fléchiss), N (effort normal), T (effort tranchant) ,Mt (moment de torsion) du système .

Dans le cas présent, l’énergie potentielle est celle emmagasinée par chacune des barres lors de sa déformation en traction ou compression.(en conséquence M,T et Mt=0)

De plus les efforts étant  constants tout le long de la barre de longueur Li , la relation générale s’écrit :

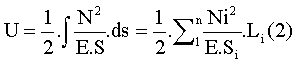
La sommation étant réalisée pour les n barres de section Si, soumises à Ni 

La conservation de l’énergie permet d’écrire que (1)=(2), on obtient la relation de Clapeyron, soit:

 

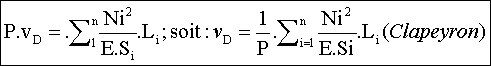
 (Equation de Clapeyron applicable si le déplacement cherché a même support que la force extérieure au point D)

 

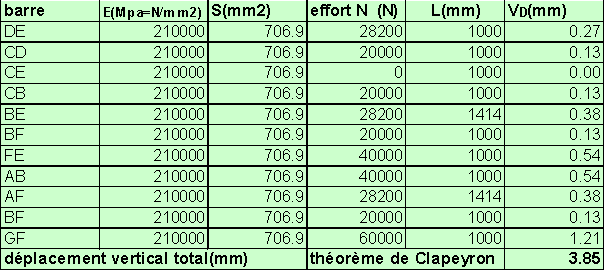
Il est intéressant de présenter les calculs dans un tableau.(voir ci-après)

 

Nous avons considéré la section Si=S  identique pour chaque barre ce qui permet de mettre ce terme en facteur dans l’expression ci-dessus.

 

La dernière colonne du tableau indique la part de flèche  résultant de la déformation de chaque barre.

Par application de la formule de Clapeyron précédente

 

Il faut donc évaluer cette expression barre après barre et faire la somme.

4-a: déplacement horizontal du point D (H_D) :

Cette fois les directions de P et du déplacement en D cherché ne sont plus identiques…

La solution la plus commode est d’utiliser le théorème  de Bertrand de Fontviolant (BdF).

Le principe de la méthode consiste à considérer 2 états de charge du même système :

Etat 0 (ou état réel) :

Poutre soumise aux forces extérieures (ici P). Nous recherchons le déplacement horizontal au point D dans cet état.

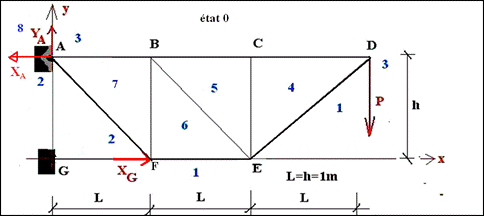
Etat 1 (« ou état fictif unitaire ») :

La même structure est soumise à une force unité appliquée au point D Cette force unité a même direction que le déplacement cherché (soit ici horizontale) 

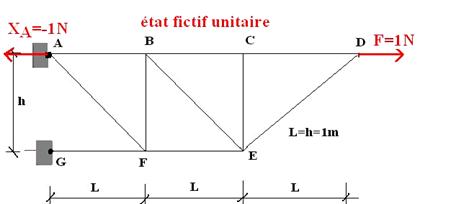
Le théorème de BdF (qui découle du théorème de Castigliano) s’énonce comme suit :

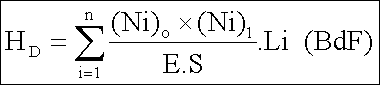
(Ni)o désigne l’effort normal dans la barre i la structure étant dans l’état 0,

(Ni)1 désigne l’effort normal dans la même barre ,la structure étant dans l’état 1.

La somme étant étendue à toute les barres.

Les efforts (Ni)0 sont reportés depuis  le tableau précédent. 

Les efforts (Ni)1 sont tous nuls sauf pour les 3 barres AB,BC,CD où ces derniers sont égaux à 1N.

Pour calculer H_D, il suffit de reprendre le tableau précédent et y ajouter la colonne des (Ni)1.

Le résultat est immédiat :

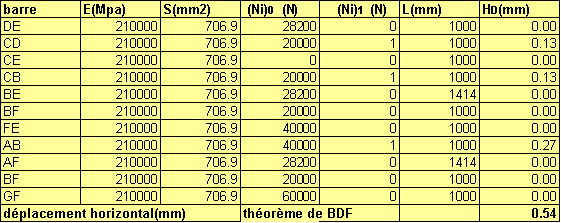
Pour vérifier ces résultats, on trouvera ci-dessous les déplacements des nœuds donnés par le logiciel RDM6.

Le point D étudié correspond au nœud 4 :

Déplacement vertical :  dy=-3,83mm ; déplacement horizontal : dx=0,539mm !

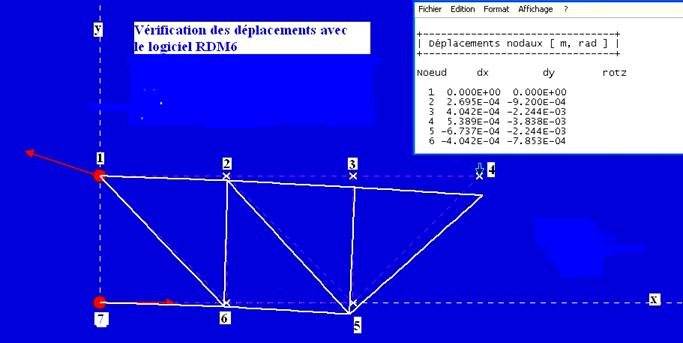
(La méthode de BDF était utilisable pour évaluer V_D ; il fallait alors considérer la poutre dans l’état réel soumise à P puis la poutre dans l’état fictif soumise en D à F=1N  force verticale et appliquer l’équation de BDF.)

(Pour obtenir les efforts dans les barres dans l’état fictif  (Ni)₁ il suffit de multiplier les valeurs Ni(o) par F/ P )

(Cette méthode permet d’obtenir les déplacements  en n’importe quel point de la structure, ce qui n’est pas le cas avec  Clapeyron)

Informations biographiques

Nom:	Eugène Bertrand de Fontviolant
Né(e) en	1861 à Romilly-sur-Seine, Aube (10),
Décédé(e) en	1954 à Vallesvilles, Haute-Garonne (31),
Education:	Diplômé de l'Ecole Centrale de Paris