III. ÉQUATIONS TRIGONOMÉTRIQUES :

On rappelle que cos (x+2k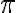$\pi$) = cosx et sin (x+2k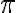$\pi$) = sinx quels que soient

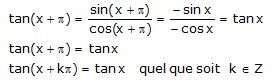
1. Equation cosx = a, a 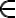$\in$ R

- Si, équation n’admet aucune solution

- Si  , on a une infinité de solution. En effet si  est solution, (c'est-à-dire ),  est aussi solution (car  )

Et comme  quel que soit est aussi solution, de même que

En admettant que ce sont les seules solutions, on a

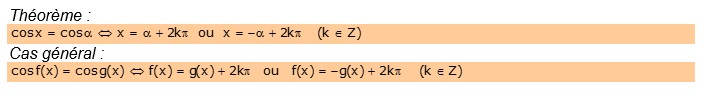
2. Equation sinx = a :

- Si  pas de solution

- Si  on a une infinité de solution

Si  est solution

Comme est aussi solution, donc  aussi

En admettant que ce sont les seules solutions on a :

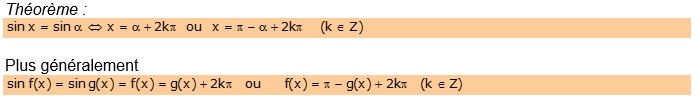
Exemple:

3. Equation acosx+ bsinx=c

Exemple

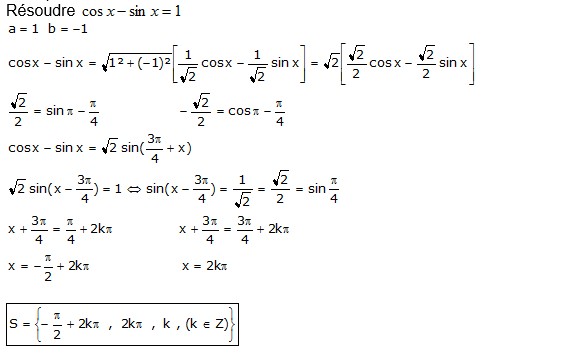
4. Equation tanx = a

Théorème :

Quel que soit le réel a, l’équation  admet toujours une infinité de solution.

5. Images des solutions d’une équation :

L’image d’une solution  d’une équation est le point M du cercle trigonométrique tel que

Si les solutions sont de la forme   les images des solutions forment un polygone régulier à n cotés inscrit dans le cercle trigonométrique.

Si n = 3, on a un triangle équilatéral

Si n = 4, on a un carré,

Si n = 5 , on a un pentagone régulier

…..

si n = 1, on un seul point

si n = 2, on a deux points symétriques par rapport à l’origine du repère

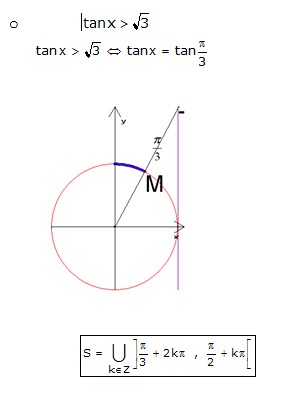
6. Exemples d’inéquation trigonométrique :

Exemples : 

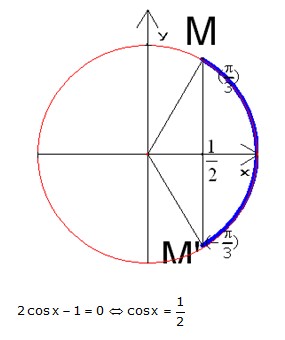
- résoudre 2cosx - 1 > 0