Séquence 2: Notion de Variation

Des boules de cotillons ont été utilisées (les mêmes que pour les simulations de désintégrations des radio-isotopes). Les sacs sont confectionnés avec des sac-poubelles.

Au départ de la manipulation les 40 boules sont enfermées dans un seul sac.

Les "génotypes" des "individus" sont constitués par tirage au sort.

Chaque sac représente un individu. Les quatre sacs des "individus" qui ne participent pas à la reproduction sont mis de côté au hasard. Les autres sont rassemblés par paires également de façon aléatoire.

Pour constituer un "descendant" on prélève une boule dans chaque sac. Un des élèves, nommé secrétaire, note les résultats et les boules sont immédiatement replacées dans leur sac d'origine.

Chacun des quatres groupes de manipulation envoie un représentant reporter au tableau les résultats. Une réflexion commune à tous les membres du groupe permet de trouver une explication à la diversité des résultats : c'est la petite taille du groupe qui l'explique.

Une confrontation avec l'étude des probabilités de transmission des allèles permet de faire émerger l'idée que les fréquences alléliques vont varier de façon importante et rapide au sein de populations de taille réduite sans que la sélection naturelle soit en jeu.

L'hypothèse de la disparition probable d'un ou plusieurs allèles est posée

Les élèves désirent généralement poursuivre l'expérience sur les générations suivantes pour le vérifier mais plusieurs obstacles se présentent.

1 Le temps imparti dans les programmes est trop court pour réaliser une manipulation significative.

2 Une simulation sur plusieurs générations demande d'attribuer un sexe à chaque individu et de réaliser des couples en conséquence.

3 Il faudrait inventer des mécanismes de simulation pour éviter les mariages consanguins et parer aux variations importantes de sex-ratio.

Pour lancer une nouvelle étape dans la réflexion on peut évoquer le cas de l'apparition d'un nouvel allèle chez l'un des individus de la première génération. Les élèves doivent formuler des hypothèses.

Relevant le défi de la simulation numérique, Quentin Martouzet, élève de Terminale S au lycée Jean Perrin de Rezé a écrit un logiciel reproduisant la manipulation effectuée en classe. Il est téléchargeable en cliquant sur le lien ci-contre.

Après installation, le programme est disponible dans "Program Files".

Télécharger le logiciel fréquences alléliques

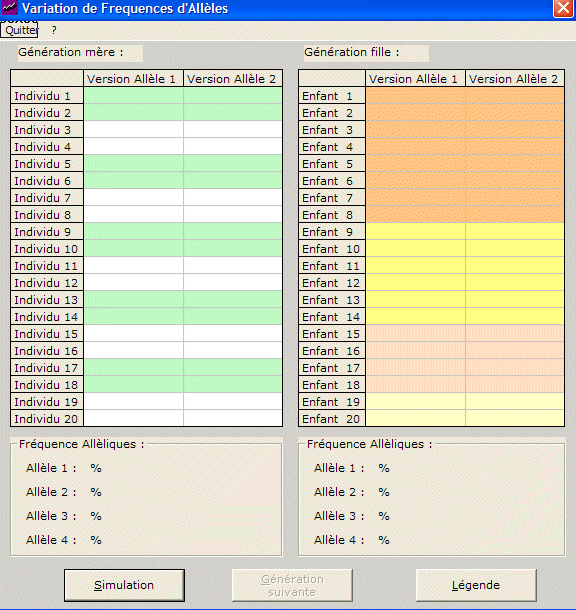
Au démarrage, aucun tirage au sort n'est effectué. En cliquant sur "simulation" on provoque la distribution des allèles à la génération des parents et la simulation de répartition des allèles chez les enfants. La procédure est strictement conforme à celle décrite dans la simulation analogique.

Dans la colonne "Parents" les deux teintes correspondent à la constitution des couples.

Dans la colonne "Génération fille" elles correspondent au rang des enfants dans les familles.

En cliquant plusieurs fois sur le bouton "Simulation" on obtient toujours des résultats différents.

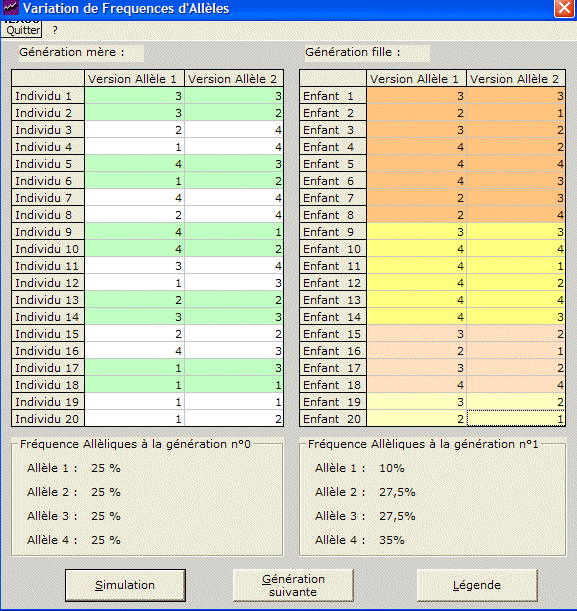
Un bouton "Génération suivante" a été ajouté. Il fonctionne en reportant dans la colonne de gauche le contenu de la colonne de droite et en refaisant la simulation de descendance cette fois-ci en refaisant des couples au hasard parmi les individu de la génération n°1.

Elle ne respecte pas les règles de constitution des couples puisque les individus ne sont pas sexués .

Tel qu'il est actuellement, ce logiciel permet de mettre en évidence que la disparition de tous les allèles sauf un est assez rapide. Lors d'une simulation nous avons constaté que la première disparition a lieu à la trente et unième génération, que la seconde disparition a lieu à la quarante sixième et qu'au bout de 100 générations un seul allèle est présent. Ces résultats sont très variables d'une simulation à une autre.

Il est possible de reporter ces résultats sur un graphique pour schématiser le phénomène appelé dérive génétique.

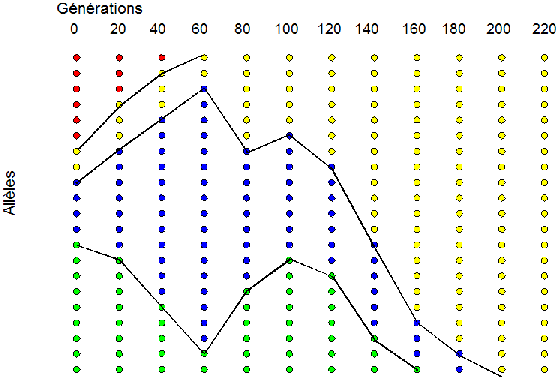
Le diagramme ci-contre représente le résultat d'une simulation sur 220 générations menée sur une population de 21 individus montrant quatre allèles différents. Le temps de coalescence (il ne reste plus qu'un seul allèle) est ici de 200 générations. Cette simulation, plus évoluée que celle qui est développée plus haut montre les mêmes résultats. En l'absence d'apport génétique externe ou de néomutations, les petites populations tendent vers l'homogénéisation génétique. (d'après André Langaney : Les Hommes passé, présent, conditionnel)

L'utilisation de la loi des grands nombres que les élèves connaissent en Terminale S conduit à affirmer que les fréquences alléliques doivent rester stables au cours du temps si tous les croisements sont équiprobables et si l'effectif de la population est infini ou supposé tel. De telles conditions ne sont jamais réalisées pour les populations d'êtres vivants et la coalescence devient inéluctable. Dans ce modèle, les néomutations ne sont pas prises en compte et le modèle suivant permet de répondre à cette objection légitime.

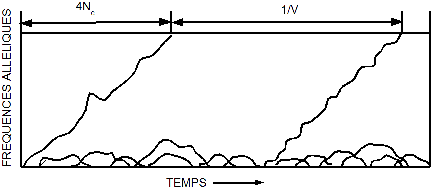
Dans cette simulation, des néomutations ont étés introduites. On voit que la plupart des allèles disparaissent rapidement mais que certains arrivent à effectuer un remplacement. Le temps de coalescence en nombre de générations est estimé à quatre fois l'effectif efficace (Ne). Le temps de remplacement d'un allèle par un autre sera égal à l'inverse du taux de mutation 1/V. Chaque nouvelle mutation neutre a la même probabilité d'arriver à la coalescence que les autres. Bien que cette probalité soit faible, la multiplication des mutations raccourci le temps de remplacement.

d'après Ridley, "écologie" d'après Kimura 1980 dans pour la science N°27