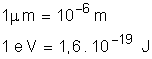Enoncé Physique série A 2010

BACCALAUREAT DE L’ENSEIGNEMENT GENERAL – MADAGASCAR

Série : A -  SESSION 2010

 

Epreuve de : Sciences Physiques

Durée : 2 heures  15 minutes 

                                                                                                                                                  

 

EXERCICE 1                   (6pts)

 

Une lame vibrante munie de deux pointes déterminer, en deux points 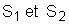 de la surface libre d’un liquide au repos, des mouvements vibration d’équation horaire :

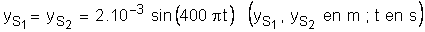
1-    a) Quel phénomène physique se produit- il à la surface libre du liquide ?                          (1 ; 1)

b) Qu’observe-t-on à la surface libre du liquide ?                                                                           (1 ; 1)

   2- La longueur d’onde est 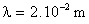. Calculer la célérité de propagation des ondes.                  (1,5 ; 1)

3- On considère un point M appartenant à la surface libre du liquide tel que 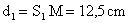 et 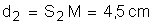. Déterminer l’équation horaire du mouvement du point M.                            (2,5 ; 1,5)

 

Pour A seulement

4- Déterminer le nombre et les positions par rapport à 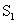 des points immobiles sur le segment  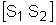(0 ;1,5)

On donne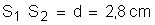 

 

EXERCICES 2 :                    (7pts)

Dans un dispositif interférentiel d’Young, le distance séparant les deux fentes fines 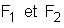 identique et parallèles, est a= 1,9 mm. L’écran E est placé à une distance D = 2 m du plan des  fentes. On éclaire le dispositif avec une radiation rouge de longueur d’onde .

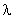1-    Expliquer le phénomène observé sur l’écran E.                                                               (1,5 ; 1,5)

2-    La dixième frange obscure se trouve à une distance d = 7,6 mm de la frange centrale.

a)    Apres avoir défini l’interfrange i, la calculer.                                                                       (1,5 ; 1)

b)    Calculer la longueur d’onde 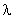 de la radiation utilisée.                                                           (2 ; 1)

3-    On éloigne l’écran E du plan des en déplaçant de 0,5 m de sa position précédente.

Déterminer la nouvelle distance de la dixième frange obscure à la frange centrale ?              (2 ; 1,5)

 

Pour A2 seulement

1)    On ramène l’écran à la distance D= 2m. Le dispositif est maintenant éclairé par une source émettant une radiation rouge de longueur d’onde 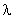 et une autre radiation de longueur d’onde  .

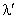On observe que la première coïncidence se produit à la 7eme frange brillante rouge et à la 8eme frange brillante de l’autre radiation. Calculer 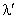 .                                                                                        (0 ; 2)

 

EXERCICE 3 :

La cathode d’une cellule photoélectrique zu potassium est éclairée par deux radiations lumineuses monochromatique de longueur d’onde respectives .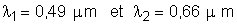

L’énergie d’extraction d’un électron de la cathode au potassium est .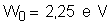

1-    Définir l’énergie d’extraction d’un électron ?                                                                                (1 ; 1)

2-    Calculer la longueur d’o, de seuil 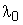 du potassium                                                                  (2 ; 1,5)

3-    Laquelle de ces deux radiations provoque-t-elle l’effet photoélectrique ?                                 (2 ; 1,5)

(Votre réponse doit être justifié)

4-    Calculer, en joule, l’énergie cinétique maximale d’un électron à la sortie de la cathode au potassium. (2 ; 1,5)

 

Pour A2 seulement

5-    Calculer la vitesse maximale d’un électron à la sortie de la cathode au potassium.                (0 ; 1,5)

On donne :

Constance de Planck :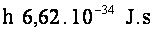

Masse d’un électron :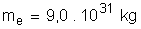 

Célérité de la lumière dans le vide :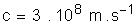 

Charge d’un électron :