Série D - Sciences Physiques

BACCALAUREAT DE L’ENSEIGNEMENT GENERAL – MADAGASCAR

Série : D -  SESSION 2007

 

Epreuve de : Sciences Physiques

Durée : 3 heures  15 minutes 

 

I - CHIMIE ORGANIQUE                 (3 pts)

Un mono alcool saturé X a pour masse molaire .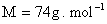

1-      Donner la formule brute et les formules semi-développées des isomères de cet alcool.

2-      Un des isomères de cet alcool, noté A est optiquement actif. Donner la formule semi-développée et le nom de A, représenter en perspective ses deux énantiomères.

3-      L’oxydation ménagée d’un deuxième isomère, noté B par une solution acidifiée de permanganate de potassium 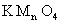 en excès, produit de l’acide butanoïque.

Après avoir identifié l’alcool B, écrire l’équation bilan de la réaction traduisant l’oxydation de cet alcool.

 

 

II - CHIMIE MINERALE                    (3 pts)

 

On considère une base 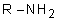 dans laquelle R est un groupe alkyle de formule .

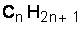1-      Ecrire l’équation de la réaction de dissolution de 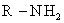 dans l’eau.                                 

2-      On prépare une solution S en dissolvant m = 2,19g de cette base dans l’eau, de façon à obtenir un litre de solution. On prélève un volume 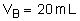 que l’on introduit dans un bécher et on y ajoute progressivement une solution d’acide chlorhydrique de concentration 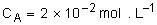. En suivant l’évolution du pH au cours de la réaction, on obtient l’équivalence acido-basique lorsqu’on a versé un volume  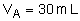de cette solution acide.

a-    Ecrire l’équation bilan de la réaction qui se produit.                                                       

     b-    Déterminer la concentration molaire CB de la solution S.

En déduire la masse molaire et la formule brute de cette base faible.  

                

                             

III - PHYSIQUE NUCLEAIRE                      (2 pts)

 

Un noyau de polonium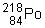  se transforme en noyau  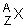 en émettant une particule a constituée de noyau d’hélium.

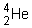1-     Calculer en MeV l’énergie de liaison par nucléon du noyau d’hélium.                                    

2-     Ecrire l’équation de désintégration du 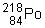en précisant les lois de conservation utilisées. 

3-     La période radioactive du 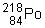 est de 3min 03s. Un échantillon renferme 2mg de  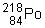à l’instant initial. Soit m la masse de 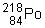qui reste à l’instant t. Reproduire et compléter le tableau suivant :

     

t	0	T	2T	3T
m(mg)

 

Données :       unité de masse atomique :     1u 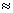   931,5 MeV.c^–2

                        masse du proton :                  mp 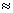   1,0073 u

                        masse du neutron :                mn 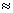    1,0087 u

                        masse du noyau d’hélium :    mHe 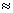 4,0015 u

Extrait du tableau de classification périodique :

IV - OPTIQUE                                               (2 pts) 

Une lentille mince convergente 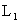, de centre optique 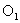, a une distance focale .

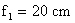1-     Un objet AB de hauteur 1cm est placé perpendiculairement à l’axe optique, à 10cm devant la lentille L1.

a-  Déterminer par calcul les caractéristiques (position, nature, sens et grandeur) de l’image A’B’ de AB.  

b-  Effectuer ensuite une construction graphique.                                                                     

(Echelle : 1/5 sur l’axe optique et en vraie grandeur pour l’objet  AB)

2-     A la lentille L1, on accole une lentille L2 de distance focale f2 pour avoir un système optique de vergence C. On maintient l’objet AB à la même position que précédemment. On obtient une image renversée deux fois plus grande que l’objet AB. Déterminer la vergence C du système optique accolé. En déduire la distance focale f2 de la lentille L2.                                                                       

 

 

V - ELECTROMAGNETISME                     (4 pts)

 

A-   Une bobine de centre O, de longueur l = 50cm et d’inductance L est formée de N = 500 spires ; le rayon de chaque spire est r = 5cm. La bobine est parcourue par un courant d’intensité

I = 50mA.

1-       Calculer l’intensité du champ magnétique créé au centre de la bobine.                                   

2-       Montrer que l’inductance L de la bobine s’écrit : 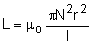 Calculer L.                            

B-     Un circuit comprend en série une bobine de résistance interne négligeable et d’inductance L = 5mH, une résistance R = 10Ω et un condensateur de capacité C. Il est soumis à une tension alternative sinusoïdale de valeur efficace U = 25V et de fréquence f = 50Hz.

1- Qu’appelle-t-on résonance d’intensité ? Déterminer la capacité C du condensateur pour qu’il y ait résonance.                                                                                                                                     

2- Calculer, dans cette condition, la valeur efficace I0 de l’intensité du courant dans le circuit, ainsi que les tensions efficaces aux bornes du condensateur et aux bornes de la bobine.                                    

On donne :  µ0 = 4 x 10–7 SI      ;      2 = 10.

 

PROBLEME DE MECANIQUE                   (6 pts) 

Les parties A et B sont indépendantes. Prendre .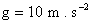

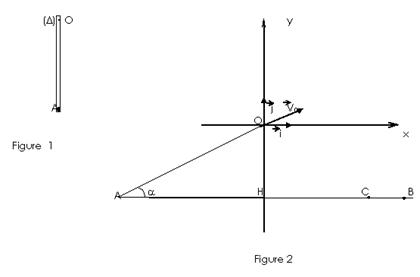
A-   Un système (S) est constitué d’une tige homogène de section constante, de longueur ℓ et de masse M. A son extrémité A est fixée une masse ponctuelle m telle que m = M/3. A l’autre extrémité O passe un axe horizontal (D) perpendiculaire au plan de la figure. On néglige les forces de frottement. (Figure 1)

1-       Montrer que la position du centre d’inertie G du système est telle que .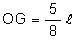       

2-       Montrer que le moment d’inertie du système par rapport à l’axe (D) est JD = 2mℓ2.     

3-       On écarte (S) de sa position d’équilibre d’un angle très petit qm et on l’abandonne sans vitesse initiale. Etablir l’équation différentielle du mouvement de (S). En déduire sa nature.             

 

B-    Un solide ponctuel de masse m = 0,1kg est lancé, à partir d’un point A avec une vitesse initiale 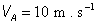, le long de la ligne de plus grande pente d’un plan incliné AO, de longueur L, faisant un angle a = 30° avec l’horizontal. (Figure 2)

Au cours de son déplacement, il est soumis à une force de frottement f, parallèle au plan incliné et de sens opposé au vecteur vitesse, d’intensité constante f = 0,1N.

1- Calculer la longueur L de la piste sachant que sa vitesse en O est  .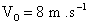        

2- Le solide quitte le plan incliné au point O à l’instant t = 0 et tombe sur le sol horizontal AB, en un point C, après avoir décrit une trajectoire C.

Etablir l’équation cartésienne de la trajectoire C  dans le repère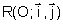  

et calculer la distance AC.