Enoncé Mathématiques série D 2000
MATHEMATIQUES - Série D - SESSION 2000
Exercice 1 (5 points)(corrigé)
P est un plan complexe rapporté à un repère orthonormal direct (O ;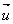 
, 
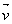). On prendra 1 cm pour unité graphique.
1.a.Résoudre dans C l’équation : z ² – (6 – i) z + 11 – 3i = 0.(0,5 pt)
b. Déterminer les nombres complexes z et z ’ tels que :
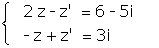(0,5 pt)
Dans tout ce qui suit, on note par A, B, C et D les points d’affixes respectives a = 3 + i, b = 3 – 2i,
c = 6 – 2i et d = 6 + i.
2.a.Placer dans P les quatre points A, B, C et D.(0,5 pt)
b.Démontrer que le triangle (BAD) est isocèle et rectangle en A, et le triangle (BCD) est isocèle et rectangle en C.(0,75 pt)
c.En déduire que les quatre points A, B, C et D se trouvent sur un même cercle (G) dont on précisera le centre W et le rayon. Tracer (G) sur la figure précédente.(0,75 pt)
3. Soit S la similitude plane directe de centre A et qui transforme B en C.
a.Préciser les éléments caractéristiques de S.(1 pt)
b.Construire sur la figure précédente le transformé de ABCD par S.(1 pt)
Exercice 2(5 points)(corrigé)
N.B. :On exprimera les résultats sous forme décimale à 10–2 près.
Le tableau suivant indique les variations du chiffre d’affaires yi d’une entreprise selon les frais de publicité xi (xi et yi sont exprimés en millions de francs malagasy) de 1992 à 1999.
|
Années |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
xi |
2 |
2,3 |
2,6 |
2,9 |
3,2 |
3,5 |
3,8 |
4,1 |
|
yi |
52 |
59 |
60 |
65 |
70 |
72 |
73 |
75 |
On donne :
; 
; 
; 
;
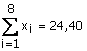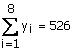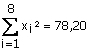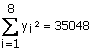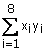=1645,10.
1.a.Représenter le nuage de points Mi(xi , yi).
(Unité graphiques :
- 2 cm représente 1 million de francs malagasy sur l’axe des abscisses.
- 1 cm représente 10 millions de francs malagasy sur l’axe des ordonnées).(1 pt)
b.Calculer les coordonnées du point moyen G et placer ce point.(0,75 pt)
2.a.Montrer que le coefficient de corrélation linéaire associé à cette série statistique est :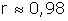 
.(1,5 pt)
b.Interpréter ce résultat.(0,25 pt)
c.Par la méthode des moindres carrés, donner l’équation de la droite de régression de y en x et tracer cette droite.(0,75 pt)
3.a.Montrer que x1, x2, …, x8 constituent les 8 premiers termes d’une suite arithmétique (xn) dont on précisera la raison.(0,25 pt)
b.Donner une estimation du chiffre d’affaires de cette entreprise en 2002.(0,5 pt)
Exercice 3(5 points)(corrigé)
N.B. :–Les questions 1. et 2. sont indépendantes.
- On donnera les résultats sous forme de fraction irréductible.
Une urne contient des boules indiscernables au toucher : rouges, vertes et noires.
1. On suppose qu’il y ait 12 boules dans l’urne dont : 3 rouges, 4 noires et 5 vertes. On tire au hasard et simultanément 3 boules de l’urne.
a.Déterminer le nombre de tirages possibles.(0,5 pt)
b. Déterminer les probabilités des événements suivants :
A : « Avoir 3 boules noires ».(0,5 pt)
B : « Avoir 3 boules de même couleur ».(0,5 pt)
C : « Avoir au moins deux boules noires ».(0,5 pt)
D : « Avoir au plus deux boules rouges ».(0,5 pt)
2. On suppose qu’il y ait 25% de boules rouges dans l’urne. On appelle « gain » l’obtention d’une boule rouge lors d’un tirage d’une boule de l’urne. L’expérience consiste à tirer au hasard et successivement 4 boules de l’urne en remettant dans l’urne chaque boule tirée avant de tirer une autre. Soit X la variable aléatoire qui à chaque expérience associe le nombre de gains.
a.Vérifier que l’univers image de X est {0, 1, 2, 3, 4}.(0,25 pt)
b.Montrer que la probabilité d’avoir 3 gains est égale à 
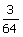.(0,5 pt)
c.Déterminer la loi de probabilité de X.(1 pt)
d.Définir la fonction de répartition F de X.(0,5 pt)
e.Si n est le nombre de boules rouges, 3n – 7 le nombre de boules vertes et 2n – 1 le nombre de boules noires dans l’urne, calculer n.(0,25 pt)
Exercice 4(5 points)(corrigé)
On considère la fonction f définie sur [ 0 ; + ¥ [ par :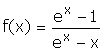 
.
On note par (C) la courbe représentative de f dans un repère orthonormé (O ;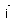 
, 
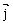), d’unité 2 cm.
1. Soit h la fonction définie sur [ 0 ; + ¥ [ par : h (x) = (– x + 2)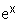 
– 1.
a.Etudier les variations de h et dresser son tableau de variation. (On ne demande pas de tracer la courbe représentative de h).(0,5 pt)
b.Montrer que l’équation h (x) = 0 admet une solution unique a dans [ 0 ; + ¥ [. Vérifier que a est compris entre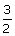 
et 2.(0,5 pt)
c.En déduire, suivant les valeurs de x, le signe de h (x).(0,5 pt)
2.a.Déterminer la limite de f en + ¥. Interpréter graphiquement ce résultat.(0,5 pt)
b.Etudier, suivant les valeurs de x, la position relative de (C) par rapport à la droite (D) d’équation y = 1. (On admet que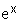 
– x > 0 sur [ 0 ; + ¥ [).(0,5 pt)
3.a.Montrer que pour tout x de [0 ; + ¥[ ,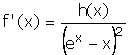 
.(0,5 pt)
b.Montrer que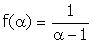 
et donner le tableau de variation de f.(0,5 pt)
c.Tracer (D) et (C) dans un même repère. (On prendra a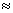 
1,84 et f (a) 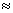1,20).(0,5 pt)
4. Soit F la fonction définie sur [ 0 ; + ¥ [ par : F (x) = l n (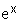 – x).
a.Calculer F ’ (x).(0,5 pt)
b.On note par A(a) l’aire du domaine plan limité par la courbe (C), l’axe (x ’Ox), les droites d’équations x = 0 et x = a. Utiliser l’égalité h (a) = 0 pour montrer que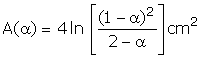 
.(0,5 pt)