Enoncé Mathématiques série D 2002
Résumé de section
-
Nous mettons à votre disposition des sujets de Mathématiques
proposés au baccalauréat série D à Madagascar
MATHEMATIQUES - Série D - SESSION 2002
N.B. : Les QUATRE exercices sont obligatoires
EXERCICE 1 ( 5 points ) corrigé
Soit le polynôme P à variable complexe z défini par : P(z) = z3 – (5 + i) z2 + (10 + 6i) z – 8 – 16i.
1°/ a) - Montrer que l’équation P(z) = 0 admet une solution imaginaire pure 
i où est un réel
que l’on déterminera. ( 0,5 pt )
b) - Mettre P(z) sous la forme (z - i ) (z2 + az + b) où a et b sont des nombres complexes que
l’on déterminera. ( 0,5 pt )
c) - Résoudre dans C l’équation P(z) = 0. ( 0,5 pt )
2°/ Dans le plan complexe (P ) muni d’un repère orthonormé direct (O ;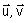 
), on considère les points
A, B, C d’affixes respectives zA = 3 + i ; zB = 2i ; zC = 2 – 2i.
a) – Placer les points A, B, C (On complètera cette figure au fur et à mesure des questions). ( 0,5 pt )
b) – On pose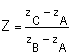 
. Donner la forme trigonométrique de Z. ( 0,5 pt )
c) – En déduire la nature du triangle ABC. ( 0,5 pt )
d) – Calculer l’affixe du point E tel que ABEC soit un carré. ( 0,25 pt )
e) – Calculer l’affixe du point D tel que ABCD soit un parallélogramme. ( 0,25 pt )
3°/ Soit S la similitude plane directe transformant A en C et laissant invariant le point B.
a) – Déterminer l’expression complexe de S et préciser ses éléments caractéristiques. ( 0,5 + 0,5 pt )
b) – Déterminer et construire l’image par S du quadrilatère ABED. ( 0,5 pt )
EXERCICE 2 ( 5 points )
Le tableau suivant indique, pour une même distance, les variations des quantités yi d’essence consommées de certaines voitures suivant leurs puissances xi (xi est exprimé en chevaux et yi en litres).
|
xi |
3 |
4 |
5 |
5 |
6 |
7 |
8 |
10 |
|
yi |
10 |
12 |
20 |
25 |
28 |
30 |
32 |
35 |
On donne :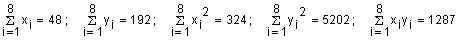 
.
1°/ a) – Représenter le nuage de points Mi (xi, yi) associé à cette série statistique dans un repère orthogonal. ( 1 pt )
* 1 cm sur l’axe des abscisses représente 1 cheval.
* 1 cm sur l’axe des ordonnées représente 5 litres.
b) – Calculer les coordonnées du point moyen G et placer ce point. ( 0,75 pt )
2°/ a) – Calculer le coefficient de corrélation linéaire associé à cette série statistique. ( 1,5 pt )
b) – Interpréter ce résultat. ( 0,25 pt )
3°/ a) – Par la méthode des moindres carrés, donner l’équation de la droite de régression (D) de y en x.
Tracer cette droite. ( 0,75 + 0,25 pt )
b) – Donner une estimation de la quantité d’essence consommée par une voiture de puissance de 12 chevaux. ( 0,5 pt )
EXERCICE 3 ( 5 points )
Une urne contient dix jetons indiscernables au toucher dont :
- cinq jetons blancs numérotés : 2, 4, 6, 8, 10.
- cinq jetons noirs numérotés : 1, 3, 5, 7, 9.
L’épreuve E consiste à tirer au hasard et successivement trois jetons de l’urne sans remettre dans l’urne
le jeton qui a été tiré.
1°/ a) – Quel est le nombre de triplets que l’on peut obtenir ? ( 0,5 pt )
b) – Calculer la probabilité de chacun des événements suivants :
A : « Les jetons tirés sont de même couleur ». ( 0,5 pt )
B : « Les numéros des jetons tirés forment dans l’ordre une progression arithmétique de raison 2 ». ( 0,5 pt )
C : « Les numéros des jetons tirés forment dans l’ordre une progression géométrique de raison 2 ». ( 0,5 pt )
2°/ Soit X la variable aléatoire qui à chaque épreuve, désigne le rang du premier jeton noir tiré. (On admet
que ce rang est 0 s’il n’y a aucun jeton noir tiré).
a) – Déterminer la loi de probabilité de X. ( 1 pt )
b) – Définir la fonction de répartition de X et la représenter graphiquement dans un repère orthogonal
(O ;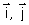 
). Unités : || 
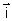|| = 1 cm ; || 
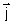||= 9 cm. ( 0,25 + 0,25 pt )
3°/ On répète 5 fois de suite et de manière indépendante l’épreuve E. A chaque épreuve, on marque 1 point
si l’on tire un jeton noir au premier coup sinon on marque 0 point.
Soit Y la variable aléatoire égale au total des points marqués à l’issue des 5 épreuves.
a) – Déterminer la loi de probabilité de Y. ( 0,5 pt )
b) – Calculer l’espérance mathématique et la variance de Y. ( 0,25 + 0,25 pt )
c) – Calculer la probabilité pour que l’on marque au moins 1 point à l’issue des 5 épreuves. ( 0,5 pt )
EXERCICE 4 ( 5 points )
On considère la fonction numérique f définie par f (x) = (x + 1) ln |x|. On note (C ) la courbe représentative de f dans un plan rapporté à un repère orthonormé (O ; 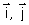) d’unité 1 cm.
1°/ a) – Déterminer le domaine de définition Df de f. ( 0,25 pt )
b) – Calculer les limites aux bornes de Df. ( 0,25 pt )
2°/ Soit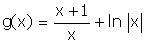 
.
a) – Etudier les variations de g (on ne demande pas la courbe représentative de g). ( 0,5 pt )
b) – Calculer g (– 1) et préciser le signe de g(x) suivant les valeurs de x. ( 0,5 pt )
3°/ a) – Calculer f ’(x) et l’exprimer en fonction de g(x). ( 0,5 pt )
b) – Dresser le tableau de variation de f. ( 0,5 pt )
4°/ a) – Montrer que le point I (1, 0) est un point d’inflexion pour la courbe (C ). ( 0,25 pt )
b) – Donner une équation de la tangente ( T ) à (C ) au point I. ( 0,25 pt )
c) – Etudier les branches infinies de (C ). ( 0,25 pt )
d) – Construire ( T ) et (C ). ( 0,25 + 0,5 pt )
5°/ Calculer, en cm2, l’aire A du domaine plan limité par (C ), l’axe (x’Ox) et les droites d’équations
x = 1 et x = e. (On pourra faire une intégration par parties). ( 1 pt )