Séquence 2: Loi de la chute libre

Correction

 

1-Commentaires et exploitation des expériences

 

L’expérience réalisée par Mathieu ne permet pas de distinguer des temps de chute différents pour les deux boules bien que les poids des objets soient très différents.

Mais l’expression du poids d’un objet est P= m.g. Or le « g » est ici identique pour les deux objets .Le temps de chute dans cette expérience serait donc indépendant de la masse de l’objet ce qui n’était pas forcément évident pour tout le monde!

 

Les caractères de la chute d’une boule d’acier et d’une feuille de papier sont par contre bien différents! La trajectoire de la feuille de papier dans l’air n’est pas verticale et sa durée de chute est plus grande! L’explication est que la feuille de papier est soumise aux frottements de l’air qui ne sont plus négligeables devant le poids .On peut donc penser que les objets ont des chutes identiques tant que les frottements restent négligeables par rapport au poids.

Ce qui est confirmé avec l’expérience sur la Lune. Le marteau et la plume ont des mouvements rigoureusement identiques.

Dans le vide, tous les corps satisfont à la même loi de chute libre. La masse n’intervient pas.

Par contre on peut observer sur la vidéo que les temps de chute identiques des deux objets sur la Lune sont plus grands que sur Terre. Le temps de chute dépend du « g » local.

 

Critiquons tout de même la première expérience : elle aurait été plus probante avec des boules de même diamètre car on pourrait conclure que la masse plus faible de la bille de bois est compensée par une meilleure pénétration dans l’air à cause de son diamètre qui est plus faible ! )

 

 

2-exploitation avec le tableur des mesures:

 

 

 

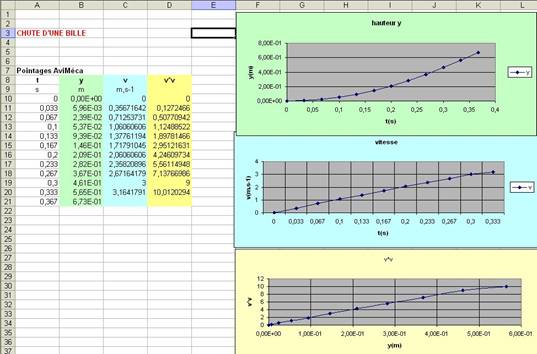
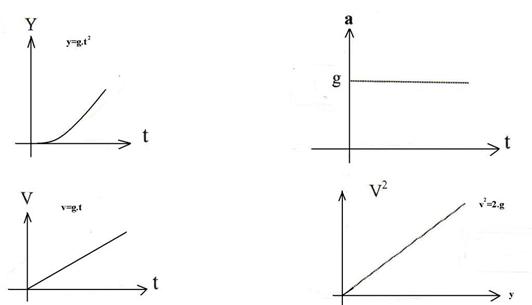
Au début de la chute, le graphe de la vitesse v=f(t) est une droite passant par l’origine (le graphe montre que la linéarité n’est plus tout à fait vérifiée au-delà de 3m.s^-1)

La position y(t) a une allure parabolique.

Les équations demandées sont :

 

Y=5t² et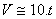

Enfin, le carré de la vitesse est une fonction linéaire de la position y soit.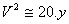

 

 

Tant qu’elle n’est pas trop grande, la vitesse est une fonction linéaire du temps (ici :v <3m.s^-1)

 

 

 

On montre qu’avec les conditions initiales les plus simples : à savoir à t=0, v=0 et y=0, les équations de la chute libre (dans le vide) s’écrivent  relativement à un repère Oy vertical orienté positivement vers le bas :

 

1- équation donnant la position à la date t: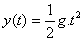

 

2- équation donnant la vitesse à la date t: v(t)= g.t.

 

3- équation donnant l’accélération : a (t)= g=constante en un lieu donné.

 

4- relation indépendante du temps entre la vitesse et l’espace parcouru : v²=2.g.y

Ces 4 équations sont celles caractérisant un mouvement rectiligne uniformément varié.

 

Remarques :

Les 3 premières équations peuvent être établies à partir de la 2éme loi de Newton en classe de terminale. Par contre la quatrième peut être établie à partir du théorème de l’énergie cinétique en classe de première (voir ci-dessous).

 

 

 

La relation (4) se déduit des expressions (1) et (2) mais elle peut aussi être établie à partir du théorème de l’énergie cinétique

Dans l’hypothèse de la chute libre, la seule force exercée sur l’objet est le poids P.

Appliquons le théorème de l’énergie cinétique entre la date t=0 et la date t :

Ec(t)-0= W(P)

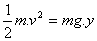( équation indépendante de m puisque m se simplifie )

Soit : v²=2 g.y

Relation en accord avec l’expérience, ce qui conforte que la chute de la bille de faible diamètre (donc peut sensible aux frottements dans l’air) peut être assimilée à une chute libre.

 

Tous les corps ont même loi de chute dans le vide (c’est alors une chute libre !)…Le corps le plus lourd comme le plus léger !…Cette observation ne nous semble pas forcément évidente car au voisinage du sol terrestre l’atmosphère perturbe beaucoup le mouvement de la plume qui n’est pas du tout celui d’une chute libre !