TP simulation « lancement de satellites ».

 

I-Introduction :sur les traces de Newton

Partie extraite d’un document de Stéphanie Hess :http://pagesperso-orange.fr/lycorsayphy/Travauxpratiques/Seconde

Dans son ouvrage, Système du monde, Newton (1642-1727) écrit :

« …plus elle (la pierre) sera projetée avec une grande vitesse, plus elle ira loin avant de retomber sur la Terre. Nous pouvons donc en déduire qu’en augmentant sa vitesse initiale elle pourra parcourir des distances de 1,2, 5, 10, 100, 1000 milles avant de retomber sur Terre, jusqu’au moment où, dépassant les limites de la Terre, elle poursuivra son parcours dans l’espace sans avoir touché le sol. »

Un boulet tiré avec une faible vitesse initiale retombe sur le sol rapidement

Un boulet tiré avec plus de puissance tombe plus loin. L'effet de courbure de la terre commence a être visible.

Un boulet tiré à très grande vitesse se satellise

2-Objectifs du TP:

-Quelle vitesse horizontale minimale faut-il communiquer à un objet pour le satelliser ? Donner les valeurs des vitesses nécessaires pour obtenir une trajectoire circulaire puis elliptique.

-Qu’est-ce qu’un satellite géostationnaire ? Quel intérêt présente-t-il ? Quelle est son altitude et sa vitesse ?

-Dans quel référentiel étudier le mouvement des satellites de  ? Le référentiel terrestre est-il le plus approprié ?

 

3-Les différents paramètres de la trajectoire :

La 1ère loi de Képler stipule que la trajectoire d’une sonde spatiale au voisinage d’un astre est toujours une conique (cercle, ellipse, parabole ou hyperbole) dont l’un des foyers est confondu avec le centre de l’astre .Cette trajectoire est relative au référentiel géocentrique de l’astre (référentiel non entrainé avec l’astre dans son mouvement éventuel de rotation propre).

Dans le cas du satellite, la trajectoire est une ellipse ou un cercle (le cercle étant un cas particulier de l’ellipse lorsque son excentricité est nulle).

L’astre considéré étant , on désignera par : R son rayon , M sa masse , h l’altitude de lancement, r_o la position initiale du satellite par rapport au centre de

 

-Remarque : les grandeurs v_o (vitesse initiale) et T (période du satellite) sont relatives au référentiel géocentrique associé à

Imaginons dont la rotation propre autour de son axe serait bloquée ! Ce solide fictif constitue un référentiel géocentrique de (*). Le référentiel géocentrique est animé d’un mouvement de translation autour du centre du Soleil.

L’étude du mouvement d’un satellite par rapport au référentiel terrestre est beaucoup plus complexe car il faut tenir compte aussi du mouvement relatif de (sa rotation autour de son axe) par rapport au référentiel géocentrique.

(*)Pour approfondir cette question, cliquer sur le lien :

Référentiels terrestre et géocentrique

 

 

4-Manipulations possibles:

 

Pour réaliser des simulations de mouvement de satellites, cliquer sur le lien suivant :

petit logiciel de physique chimie pour le lycée

ouvrir le logiciel et demander le paragraphe : « mouvement de satellites »

Avant chaque lancement, il suffira de régler v_o et r₀.

(Il est recommandé de demander le tracé des vecteurs force et vitesse )

 

 

Remarque: ayant ouvert le logiciel, il est nécessaire de revenir au texte du TP pour suivre le protocole proposé . Et vice versa.

Il suffit pour cela de mettre en réduction la page ouverte du logiciel .

En cliquant dans la barre des taches (en bas de l’écran) sur le document ouvert réduit, on peut réaliser des « allers et retours » entre le texte et le logiciel .

 

a- Détermination de la vitesse v_o nécessaire pour obtenir une satellisation circulaire en orbite basse (cas de la « navette spatiale » apportant des éléments à la station orbitale internationale « ISS »)

Après ouverture du logiciel :

-Choisir l’option « au voisinage de la Terre » avec v_o =1km/s, lancer le satellite en appuyant sur « action ». Celui-ci retombe sur le sol, sa vitesse n’est pas suffisante !

Augmenter v_o, jusqu’à obtenir une satellisation circulaire. Une telle vitesse (proche de 8km/seconde) ne peut être obtenue quand dehors de l’atmosphère où les frottements sont nuls ; d’où la nécessité d’utiliser une fusée capable d’emporter carburant + comburant pour le lancement du satellite.

 

-Quitter la page (clic sur « retour ») et choisir l’option « loin de la Terre ».

Prendre r_o légèrement supérieur au rayon terrestre (par exemple :7500km) et donner à v_o la valeur de 7.5km/s. Lancer le satellite(« action »)

Comparer le mouvements du satellite et le mouvement de rotation propre de (point rouge et repère jaune). Constater que la période du satellite est petite par rapport à la période de rotation propre de faut en effet environ deux heures pour que la station ISS repasse au dessus d’un même méridien de

Choisir une valeur plus grande de r ; constater que pour maintenir la trajectoire circulaire, il faut modifier v_o.

Cette observation est-elle en accord avec la formule du cours ?

 

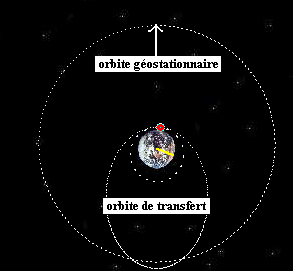
b- Orbite géostationnaire :

Sur une telle orbite, le satellite est immobile par rapport au sol ;il est alors utilisé comme relais de télécommunication pour une région donnée de

Un satellite géostationnaire gravite, dans le référentiel géocentrique, sur une trajectoire circulaire dont le centre est confondu avec celui de , dans le plan de l’équateur terrestre et dans le sens de rotation de autour de son axe. Sa période de révolution est égale à la période sidérale (ou jour sidéral**) de  (soit:86164s).

 

Il reste donc continuellement à la verticale d’un même lieu de l’équateur.

Un calcul simple permet de trouver r voisin de 42 500 km. Régler alors la vitesse pour que la trajectoire soit circulaire. Lors de l’animation, le satellite doit toujours rester au dessus du repère lié au sol et la trajectoire doit être circulaire. Ajuster r et v pour qu’il en soit ainsi. N’effacer pas la trace du satellite, elle permettra ensuite de la comparer à l’orbite de transfert.

c- Orbite de transfert :

 

C’est l’orbite qui permet au satellite de rejoindre l’orbite géostationnaire (r_rmax voisin de 42500km) à partir de sa trajectoire circulaire initiale de lancement (r=7500km) .La trajectoire est alors elliptique (l’excentricité est comprise entre 0 et 1) .La vitesse v_o nécessaire est proche de 10km/sec.

Le point de la trajectoire le plus proche de est l’apogée ; le point le plus éloigné le périgée.

Constater que le mouvement n’est plus uniforme : la vitesse est maximum à l’apogée et minimum au périgée. Ce résultat est en accord avec la loi des aires (2^ème loi de Képler)

 

d- sonde interplanétaire :

Augmenter v jusqu’à ne plus obtenir de retour de la sonde. La trajectoire est parabolique. Si l’on augmente encore v, la trajectoire devient hyperbolique.

 

 

** Le « jour sidéral » est la durée d’un tour de autour de son axe ce qui représente un peu moins de 24heures. La durée de 24heures est celle du « jour solaire » :c’est la durée entre 2 passages consécutifs du Soleil à la verticale d’un point de un jour Solaire, effectue un peu plus d’un tour sur elle-même parce qu’elle tourne aussi pendant ce temps un peu autour du Soleil.

 

Pour mieux comprendre cette notion, cliquer sur le lien suivant :

période solaire et période sidéral