Enoncé Mathématiques série C 2004
Baccalauréat de l'enseignement général
Madagascar
Session 2004
mathematiques – Série : C
N.B. : - L’Exercice et les DEUX Problèmes sont obligatoires.
- Machine à calculer autorisée.
Exercice (4 points)
I) Un dé cubique a quatre faces numérotées 0 et deux faces numérotées 1. Quand on lance ce dé, toutes les faces ont la même probabilité d’apparition.
1.- On lance ce dé une fois. Calculer les probabilités des événements suivants :
A : « La face supérieure du dé porte le numéro 0 ». (0,50 pt)
B : « La face supérieure du dé porte le numéro 1 ». (0,25 pt)
2.- On lance ce dé cinq fois de suite ; les lancers étant indépendants, calculer les probabilités des événements suivants :
C : « Le numéro 0 apparaît exactement une fois ». (0,50 pt)
D : « Le numéro 1 apparaît exactement cinq fois ». (0,25 pt)
E : « Le numéro 0 apparaît au moins une fois ». (0,50 pt)
II) 1.- a) Convertir dans la base 10 l’entier x écrit dans le système binaire : 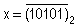 . (0,25 pt)
. (0,25 pt)
b) Convertir dans le système binaire l’entier naturel y ' 23 de la base 10. (0,25 pt)
2.- a) Dresser la table de multiplication et la table d’addition de Z/2Z. (0,25 + 0,25 pt)
b) Résoudre dans Z/2Z l’équation à une inconnue (0,50 pt)
c) Résoudre dans Z/2Z x Z/2Z le système de deux équations à deux inconnues x et y
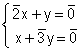 (0,50 pt)
(0,50 pt)
Problème 1 (7 points)
On considère un triangle (ABC) rectangle en A avec mes 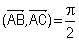 et AB ' 2AC ' 8 cm.
et AB ' 2AC ' 8 cm.
Soient I, J et E les milieux respectifs des segments [AB], [AC] et [BC].
PARTIE A
1.- a) Déterminer et construire le barycentre G du système des points pondérés {(A, ‒1), (B, 1), (C, 1)}. (0,50 pt)
b) Exprimer 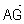 en fonction de
en fonction de 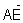 et calculer la distance AG. (0,25 + 0,25 pt)
et calculer la distance AG. (0,25 + 0,25 pt)
c) Montrer que le point E est le centre du cercle circonscrit au triangle (ABC). (0,25 pt)
d) Construire le point D tel que (ABDC) soit un rectangle et déterminer 2 isométries affines qui laissent globalement invariant le rectangle (ABDC). (0,25 + 0,25 pt)
e) Déterminer et construire l’ensemble (C) des points M vérifiant : ‒ MA2 + MB2 + MC2 = 20. (0,50 pt)
Vérifier que E appartient à (C). (0,25 pt)
2.- Montrer que pour tout point M du plan contenant A, B et C 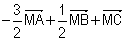 est un vecteur fixe
est un vecteur fixe 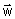 que l’on précisera. Construire le point K tel que
que l’on précisera. Construire le point K tel que 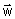 =
= 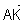 . (0,25 + 0,25 pt)
. (0,25 + 0,25 pt)
PARTIE B
Le plan complexe (P ) est rapporté à un repère orthonormé (A, 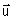 ,
, 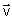 ) tel que
) tel que 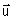 =
= 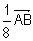 ,
, 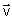 =
= 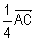 .
.
Soient S1 la similitude plane directe qui transforme C en C et I en A ; S2 la similitude plane directe qui transforme I en I et A en C.
1.- Déterminer zA, zB, zC, zI affixes respectives des points A, B, C et I. (0,50 pt)
2.- a) Déterminer les expressions complexes de S1 et S2. (0,5 + 0,5 pt)
b) Préciser les éléments caractéristiques de ces deux similitudes directes. (0,5 + 0,5 pt)
3.- Soit R = S2 o S1.
a) Préciser l’image de I par R. (0,25 pt)
b) Donner l’expression complexe associée à la transformation ponctuelle R. (0,50 pt)
c) En déduire ses éléments géométriques. (0,25 pt)
4.- Soit g la transformation ponctuelle réciproque de S1.
Caractériser g et trouver la représentation complexe associée à g. (0,25 + 0,25 pt)
Problème 2 (9 points)
Pour tout n élément de IN*, on considère la fonction fn définie par :
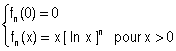 .
.
On note (Cn) la courbe représentative de fn dans un repère orthonormé (O, 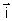 ,
,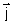 ) d’unité : 2 cm.
) d’unité : 2 cm.
PARTIE I
On désigne par In = 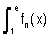 dx , n
dx , n IN*.
1.- Calculer I1. (0,50 pt)
2.- A l’aide d’une intégration par parties,
a) Calculer I2. (0,25 pt)
b) Donner une expression de In+1 en fonction de In. (0,50 pt)
c) En déduire I3. (0,25 pt)
PARTIE II Etude des fonctions fn pour n fixé
A/ 1.- a) Montrer que fn est continue en 0. (0,25 pt)
b) Etudier la dérivabilité de fn en 0. (0,25 pt)
c) En déduire la tangente à (Cn) au point d’abscisse x0 = 0. (0,25 pt)
2.- Montrer que l’équation fn+1(x) ‒ fn(x) = 0 admet trois solutions dans l’intervalle [0, +[. (0,50 pt)
En déduire que toutes les courbes (Cn) passe par 3 points fixes dont on précisera les coordonnées. (0,25 pt)
B/ Variation de fn , pour n 2.
1.- Calculer 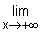 fn(x). (0,25 pt)
fn(x). (0,25 pt)
2.- Montrer que pour tout x > 0 : 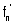 (x) = [n + ln x] [ln x]n־1. (0,50 pt)
(x) = [n + ln x] [ln x]n־1. (0,50 pt)
3.- Pour n impair
a) Montrer que 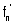 (x) et [n + ln x] sont de même signe. (0,25 pt)
(x) et [n + ln x] sont de même signe. (0,25 pt)
b) Dresser le tableau de variation de fn. On calculera en particulier fn(e־n). (0,50 + 0,25 pt)
Application : Dresser le tableau de variation de f3. (0,25 pt)
4.- Pour n pair
a) Montrer que :
- pour tout x ]0, e־n[ U ]1, +
[
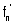 (x) > 0. (0,25 pt)
(x) > 0. (0,25 pt)
- pour tout x [e־n, 1]
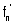 (x)
(x) 0. (0,25 pt)
b) Dresser le tableau de variation de fn. (0,50 pt)
Application : Dresser le tableau de variation de f2. (0,25 pt)
5.- Etudier les positions relatives de (C2) et (C3) respectivement dans les intervalles ]1, e[ et [e, +[.
(0,25 + 0,25 pt)
6.- Montrer que le point I(1, 0) est un point d’inflexion de (C3). (0,25 pt)
7.- Tracer dans un même repère (C2) et (C3). (0,50 + 0,50 pt)
C/ On note g la restriction de f2 à l’intervalle [1, e].
1.- Montrer que g est une bijection de l’intervalle [1, e] sur un intervalle J que l’on déterminera. (0,25 pt)
2.- Calculer (g־1)’ (e), g־1 étant la fonction réciproque de g. (0,25 pt)
3.- Représenter graphiquement g־1 dans le même repère que (C2) et (C3). (0,50 pt)
On donne : e־3 ≈ 0,05 ; e־2 ≈ 0,13 ; e ≈ 2,7.