Chapitre 2: TRAVAIL SUR PLANCHETTE

3- CONSTRUCTIONS GÉOMÉTRIQUES

A Propos

  En dessin technique, les traces doivent être faites avec précision. Dans ce cas, il est nécessaire de les tracer avec les matériels de précision tels que le compas, la règle, la règle T, l’équerre, …etc.

3.1-        Perpendiculaires

Perpendicularité des droites ou ligne horizontale: emploi du règle T et de l'équerre

  • Tracer la perpendiculaire au milieu d'un segment (A et B) de la figure ci-après:

p

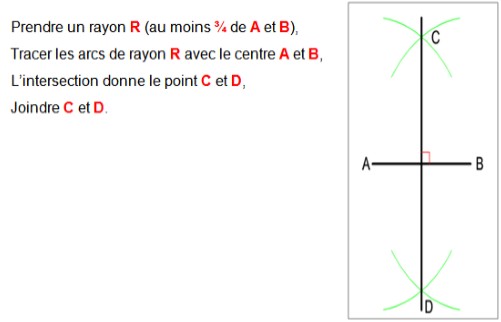
Figure 01: Construction de la perpendiculaire sur un segment

  • Tracer la perpendiculaire en un point J sur une droite:

o

Figure 02: Construction de la perpendiculaire sur une droite

  • Tracer la droite perpendiculaire au bout d'un segment non prolongeable:

Tracer un cercle de centre I (point quelconque) qui n'appartient pas au segment [AB] donné, passant par le point B (bout de ce segment).

Noter C le point d'intersection du segment et le cercle.

Tracer un segment de ce cercle qui est le diamètre et noter CD,

Tracer une droite passant par le point D et l'extrémité de segment [AB] donné,

Donc on a une droite perpendiculaire au point de ce segment.

 p

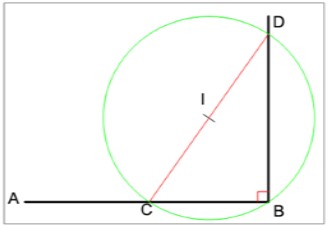Figure 03: perpendiculaire au bout d'un segment non prolongeable

3.2-        Parallèles

Perpendicularité des droites ou horizontale et verticale: emploi du règle T et de l'équerre.

  • Tracer le parallèle d'une droite (\Delta ) à une distance h donné:

En traçant une droite tangente aux deux cercle de rayon R sur une même droite et de centre A et B, avec R=h (h: hauteur donnée), on obtient un parallélisme.

r

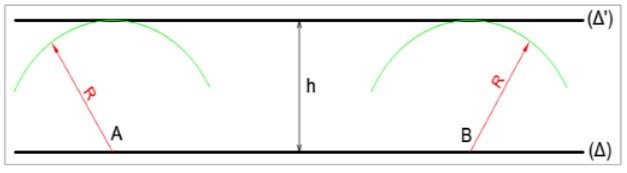
Figure 04: Construction des droites parallèles

Si on veut plus de précision, en élevant de A et B deux perpendiculaires et en portant sur celle-ci la distance h donnée, la droite (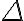\Delta ') est ainsi déterminée par deux points C et D.

r

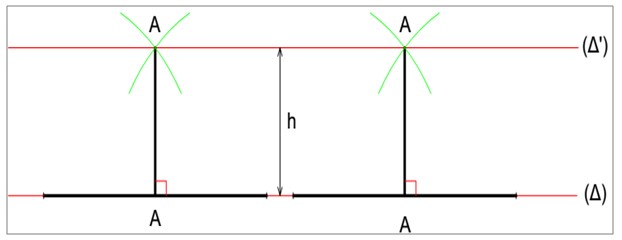
Figure 05: Construction de parallélisme avec plus de précision

3.3-        Tangentes 

La tangente est perpendiculaire à l'extrémité du rayon qui aboutit au point de contact.

  • Tracer la tangente d'une circonférence à un point A à l'extérieure

Joindre AO, tracer le diamètre AO (déterminer le point J, milieu de OA)

Tracer la circonférence de centre J et de rayon OJ coupant la circonférence de centre O et de rayon R.

Mettre T1 et T2 les intersections de ces deux cercles et joindre AT1 et AT2.

 m

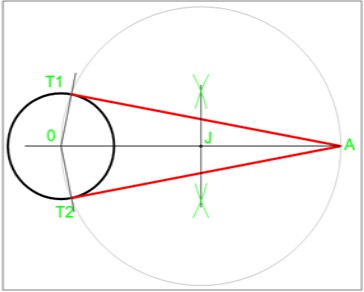Figure 06: tangente d'une circonférence en un point à l'extérieure

  •    Tracer les tangentes communes extérieures à deux circonférences données:

f

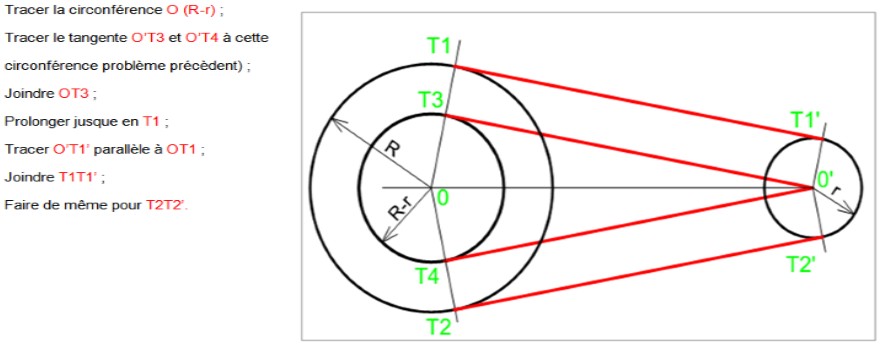
Figure 07: Tangentes communes extérieures à deux circonférences

  • Tracer les tangentes communes intérieures à deux circonférences:

Même solution que le problème précédent, mais une circonférence O (R+r)

f

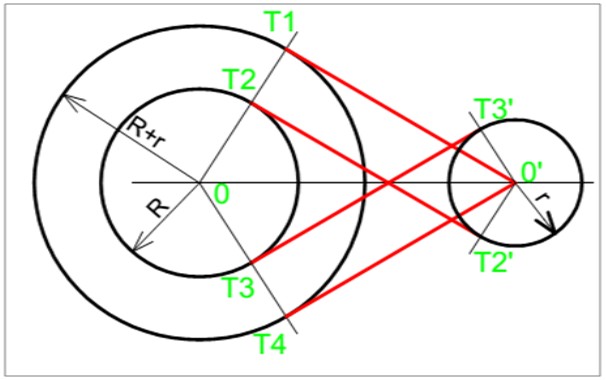
Figure 08: tangentes communes intérieures à deux circonférences

3.4-        Raccordements :

a - Méthodes de tracés manuels en dessin industriel

Si les tracés n'exigent pas une précision particulière, l'utilisation d'un gabarit ou d'un trace-cercles suffit pour donner des résultats satisfaisants. Pour des tracés plus précis, les méthodes décrites dans les paragraphes suivants sont utilisables.

b - Tracé d'un arc de raccordement de rayon R entre deux lignes quelconques

La méthode est applicable à tous les types d'angles: aigu, droit ou obtus.

Ordre des tracés:

  • parallèle à la ligne 1 situé à la distance R de celle-ci,
  • parallèle à la ligne 2 situé à la même distance R de celle-ci,
  • point d'intersection J des deux parallèles précédentes,
  • perpendiculaire JT1 à la ligne 1,
  • perpendiculaire JT2 à la ligne 2,
  • l'arc de raccordement cherché T1T2 de centre J et de rayon R.

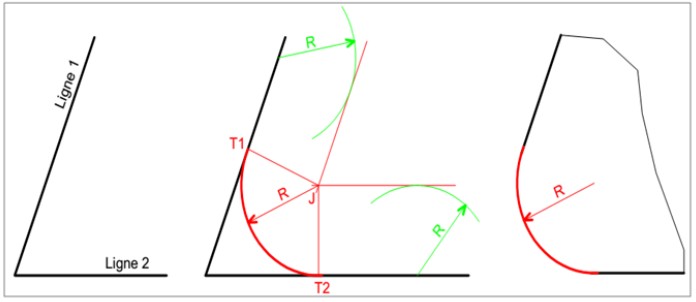
construction

Figure 09: raccordement de rayon R entre deux lignes 1 et 2

c - Tracé d'un arc de raccordement de rayon R entre une ligne et un cercle (ou arc)

Ordre des tracés:

  • la parallèle à la distance R de celle-ci,
  • le cercle de centre O et de rayon Ro + R,
  • le point d'intersection J entre le cercle et la ligne,
  • la droite OJ qui coupe le cercle initial en T1,
  • la perpendiculaire JT2 à la ligne initiale,
  • l'arc cherché T1T2 de centre J et de rayon R

f

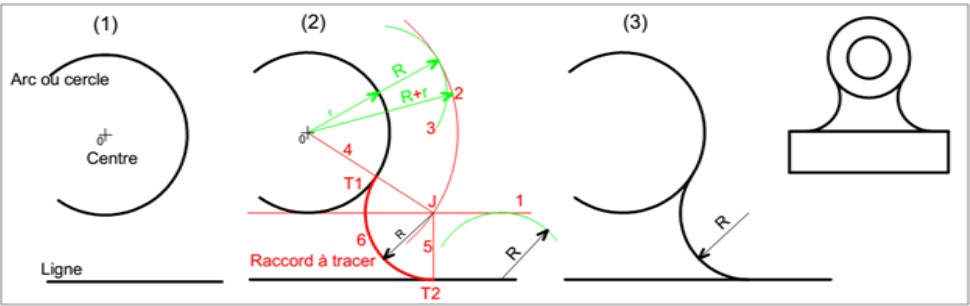
Figure 10: raccordement de rayon R entre une ligne et un cercle (ou arc)

d - Tracé d'un arc de raccordement de rayon R entre deux cercles (ou deux autres arcs)

Ordre des tracés:

  • le cercle de centre O1 et de rayon R1 + R,
  • le cercle de centre O2 et de rayon R2 + R,
  • le point d'intersection J des deux cercles précédents,
  • la droite O1J qui coupe son cercle en T1,
  • la droite O2J qui coupe son cercle en T2,
  • l'arc cherché T1T2 de centre J et de rayon R.

f

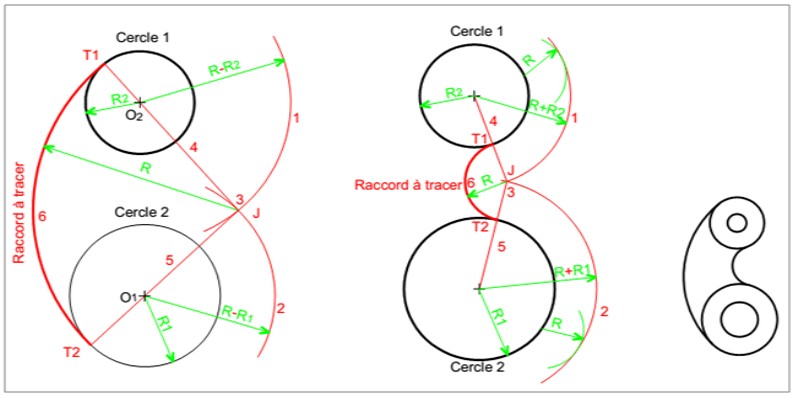
Figure 11: raccordement de rayon R entre deux cercles (ou deux autres arcs)

HAUT
Modifié le: Wednesday 3 August 2016, 12:22