Biométrie
GÉNÉTIQUE ET HÉRÉDITÉ
Biométrie
Entre les enfants et leurs parents, on note généralement une certaine ressemblance que traduit le mot hérédité. Mais les enfants présentent aussi des caractères différents de ceux de leurs parents et deux enfants nés des mêmes parents ne sont jamais absolument semblables : ce sont ces différences que traduit le mot variation.
Naturellement, l’étendue de la variation s’accroit si l’on quitte le domaine de la famille pour celui de la race, de l’espèce.
La biométrie est une méthode statistique appliquée à la biologie pour étudier quantitativement la variation au sein d’une population.
1-Analyse d’une distribution de fréquence
Série discontinue
Le nombre de loges de capsule de coquelicot varie de 6 à 20 : on répartie cette population en 15 classes ayant respectivement 6, 7, 8, ……….20 loges ; on aboutit à la distribution suivante :
|
C Classe Xi xi (n nombre de loges) |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
E Effectifs ni ni (n nombre de capsules ayant ce nnombre de loges) |
3 |
11 |
38 |
106 |
152 |
238 |
305 |
315 |
302 |
234 |
128 |
50 |
19 |
3 |
1 |
Le nombre de loges étant nécessairement un nombre entier, la série est dite discontinue
Série continue
Le diamètre de chaque coquille des petits Gastéropodes marins est mesuré à mm près à l’aide d’un pied à coulisse, la population est répartie en classes délimitées par des intervalles égaux de dimensions : 116 à 120 dixièmes de mm, de 121 à 125 dixièmes de mm, etc… Chaque classe est définie par une valeur centrale : 118, 123, etc… On a la distribution suivante :
|
Classe xi |
Valeurs limites |
116 à 120 |
121 à 125 |
126 à 130 |
131 à 135 |
136 à 140 |
141 à 145 |
146 à 150 |
151 à 155 |
156 à 160 |
161 à 165 |
|
|
Valeurs centrales |
118 |
123 |
128 |
133 |
138 |
143 |
148 |
153 |
158 |
163 |
|
Effectifs ni (nombre d’individus appartenant à chaque classe) |
|
18 |
29 |
55 |
107
|
82 |
61 |
26 |
3 |
3 |
Entre 116 et 165 dixièmes de mm, toutes les valeurs sont possibles, la série est dite continue
2- Représentation graphique d’une distribution de fréquence
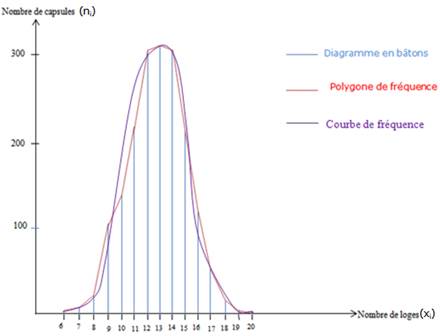
Diagramme en bâtons : sur deux axes de coordonnées, porter les classes des x en abscisse et les fréquences n correspondantes en ordonnée. A chaque classe correspond un point ; relier chaque point à l’axe des abscisses par un trait vertical ou bâton
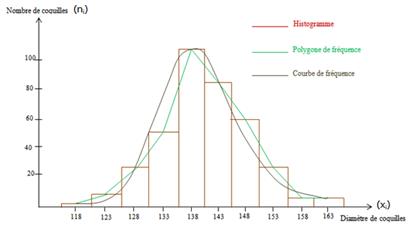
Histogramme : Porter à l’abscisse les limites des classes x et en ordonnés les fréquences correspondantes n : Chaque limite de classe étant marquée par un trait vertical, on dessine une série de rectangles dont les hauteurs sont proportionnelles aux effectifs
Polygone de fréquence : Relier les extrémités des bâtons ou les milieux des côtés libres de l’histogramme par des segments de droite
Courbe de fréquence : On passe du polygone à la régularisation des contours. Cette opération, difficile à réaliser de façon rigoureuse, peut être faite approximativement, à la main levée, en veillant à ce que les aires délimitées par le polygone et la courbe soient équivalentes de part et d’autre de celui-ci.
Lorsque la courbe de fréquence a la forme caractéristique d’une cloche, elle est dite courbe de Gauss : unimodale et symétrique
Diagramme en bâtons polygone et courbe de fréquence sur l’étude de nombre de loges de capsules
Histogramme, polygone et courbe de fréquence sur l’étude de diamètres des coquilles![]()
3- Paramètres caractéristiques d’une distribution de fréquence
Mode c’est la valeur de xi correspondante à ni maximum. Il n’est pas toujours unique, on peut avoir deux ou même plusieurs modes ; ainsi, la courbe peut être uni-, bi- ou plurimodale
Moyenne arithmétique
![]()
Variance
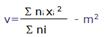
Ecart-type
![]()
Tableaux de distribution de fréquence sur l’étude de variation des diamètres des coquilles
|
Classes (en dixièmes de mm) |
Centres des classes xi |
Effectifs ni |
ni xi |
ni xi2 |
|
116-120 |
118 |
1 |
118 |
13924 |
|
121-125 |
123 |
8 |
984 |
121032 |
|
126-130 |
128 |
29 |
3712 |
475136 |
|
131-135 |
133 |
55 |
7315 |
972895 |
|
136-140 |
138 |
107 |
14766 |
2037708 |
|
141-145 |
143 |
82 |
11726 |
1676818 |
|
146-150 |
148 |
61 |
9028 |
1336144 |
|
151-155 |
153 |
26 |
3978 |
608634 |
|
156-160 |
158 |
3 |
474 |
74892 |
|
161-165 |
163 |
3 |
489 |
79707 |
|
|
ni = 375 |
ni xi = 52590
|
ni xi2 = 7396890 |
Mode=138
![]()
![]()
![]()
4- Interprétation biologique des résultats
Du point de vue théorie, la connaissance des valeurs m et permet de définir exactement l’équation de la courbe de fréquence et, par suite, de tracer cette courbe avec précision :
-les points d’abscisses m - et m + correspondent aux points d’inflexion de la courbe.
-pour une population homogène, les points d’abscisses m - 2 et m + 2 encadrent 95% de l’effectif total, ce qui permet d’affirmer au risque de 5% que la valeur du caractère étudié est comprise entre m - 2 et m + 2.
(Cas des diamètres des coquilles
m-2=140,24-2x7, 60=125,04
m+2=140,24+2x7, 60=155,44
Effectif inférieur à 125,04 : 1+8=9
Effectif supérieur à 155,44 : 3+3=6
Effectif au-delà de m-2 et m+2 : 9+6=15 qui représentent 4% de l’effectif total alors 96% de la population sont encadrés par m-2 et m+2 donc on a une population homogène)
Dans ce cas, la courbe a la forme caractéristique d’une cloche elle est unimodale; le mode est très proche de la moyenne arithmétique
Du point de vue pratique, la méthode biométrique est utilisée par les biologistes (agronomes et éleveurs) pour l’analyse de la variation :
Complétée par des essais de sélections, la méthode biométrique permet de vérifier l’hétérogénéité des populations.
Sélection : elle consiste à isoler les individus des classes extrêmes, de les laisser reproduire, de faire une distribution de fréquence de la descendance : déterminer le nouveau mode et tracer le polygone de fréquence ; On répète la même opération jusqu’à ce que le mode et le polygone de fréquence ne varie plus ; à ce moment-là on a une population appartenant à une lignée pure pour ce caractère.
Dans une lignée pure, la sélection n’est plus efficace