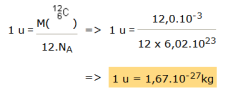NOYAU ATOMIQUE

1. Relation d'Einstein

En 1905, en élaborant la théorie de la relativité restreinte, Einstein postule que la masse est une des formes que peut prendre l'énergie.

Postulat d'Einstein: Un système de masse m possède lorsqu'il est au repos, une énergie:

E = m.c²

avec

E: énergie du système en joules (J)

m: masse du système en kilogrammes (kg)

c: vitesse de la lumière dans le vide (c=3,0.10⁸m.s^-1)

Conséquence: Si le système (au repos) échange de l'énergie avec le milieu extérieur, (par rayonnement ou par transfert thermique par exemple), sa variation d'énergie ΔE et sa variation de masse Δm sont liées par la relation: ΔE = Δm.c²

Remarque:

Si Δm<0 alors ΔE<0: le système fournit de l'énergie au milieu extérieur.

Si Δm>0 alors ΔE>0: le système reçoit de l'énergie du milieu extérieur.

2. Unités de masse et d'énergie

Le joule est une unité d'énergie inadaptée à l'échelle microscopique. On utilise plutôt à cette échelle l'électron- volt (noté eV):

1 eV= 1,60.10^-19 J

Remarque: On utilise aussi le MeV: 1MeV = 10⁶eV = 1,60.10^-13J.

A cette échelle, il est possible d'utiliser comme unité de masse l'unité de masse atomique (notée u). L'unité de masse atomique est définie comme étant égale au douzième de la masse d'un atome de carbone .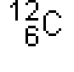

3. Défaut de masse du noyau

Expérimentalement, on a constaté que la masse du noyau atomique est inférieure à la somme des masses des nucléons qui le constituent. Dans le cas d'un noyau , en notant m_p la masse du proton et m_n la masse du neutron, on peut écrire: m_noyau < Z.m_p + (A - Z).m_n.

On pose:

Δm = Z.m_p + (A - Z).m_n - m_noyau

avec

Δm: défaut de masse du noyau

On remarquera que Δm>0.

Exemple: Dans le cas du noyau d'hélium 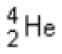, Δm = 2.m_p + 2.m_n - m().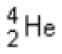