DIFFRACTION
ET INTERFERENCES
http://www.ac-nice.fr/clea/lunap/html/Interf/InterfEnBref.html
(D'après un article de G. Paturel, Cahiers
Clairaut n°87, p4, 1999)
Nous considérons la lumière comme
une onde. Que se passe-t-il quand deux ondes se rencontrent ? Deux ondes qui se
rencontrent vont interagir entre elles. Ont dit qu'elles interfèrent. Voyons
cela de plus près.
Les interférences
Imaginons deux sources émettant
une onde chacune. Nous supposerons que ces ondes sont en phase. Cela signifie
qu'au moment de leur départ, les deux ondes sont dans le même état. Si on se
rappelle que la période d'une onde lumineuse est de l'ordre de un millionième
de milliardième de seconde, ce ne doit pas être facile pour créer deux ondes
parfaitement synchrones. En fait on utilise couramment une source et son image,
ce qui permet ainsi d'avoir deux sources synchrones. Une autre condition qu'il
est important de satisfaire est d'avoir deux ondes de même fréquence. Nous
verrons cependant qu'il est possible de voir des interférences sans cette
condition (voir les activités proposées). Mais poursuivons les explications.
|
|
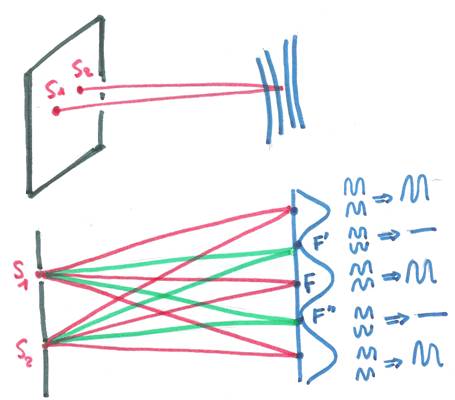
Observons la figure
ci-dessus. Quand les deux ondes arrivent en F, elles ont parcouru exactement le
même chemin. Elles sont parfaitement en phase. On a donc une source deux fois
plus intense en ce point. Si on s'écarte de F suffisamment, l'un des trajets
sera plus long, l'autre plus court. Les longueurs d'onde lumineuses ordinaires
étant très petites (quelques centaines de nanomètres) il ne faut pas beaucoup
d'écart entre les deux chemins lumineux pour faire un décalage d'une demi- longueur
d'onde. Quand cela se produira, les deux ondes seront opposées et s'annuleront.
C'est ce qui se produit en F' et F". Si on considère des écartements de
plus en plus grands, il arrivera un moment où, à nouveau, les ondes seront en
phases, puis, à nouveau, où elles s'annuleront, etc. Le résultat sera une
alternance de régions lumineuses (ondes en phase) et de régions sombres (ondes
décalées d'une demie longueur d'onde - dites en
opposition de phase).
La diffraction
Maintenant que nous avons compris
comment fonctionnent les interférences, nous allons pouvoir comprendre la
diffraction. Ce phénomène est particulièrement important en astronomie. Il
permet de comprendre la limite de résolution des lunettes et des télescopes, ce
qui ouvre la voie de l'optique moderne.
|
|
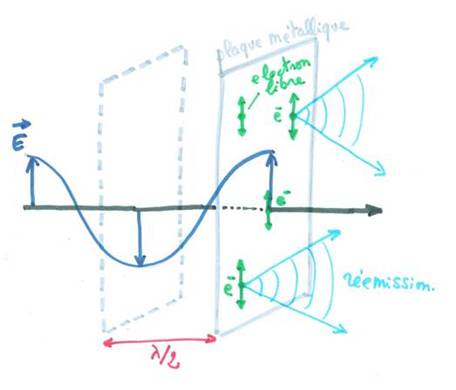
Pour commencer, posons- nous
la question suivante : Comment une onde agit-elle sur une surface métallique
plane (comme un miroir plan) ?
Nous avons vu (lumière) qu'une onde lumineuse est un champ électrique
oscillant. En présence d'un champ électrique, un électron subit une force (F
= e E), donc une accélération. Or un électron
accéléré crée un champ électrique E', donc une onde.
Tous les électrons libres de la surface métallique sont mis en mouvement de
va-et-vient sous l'effet de l'onde lumineuse. L'onde est absorbée, mais les
électrons, en oscillant, vont tous réémettre à la même fréquence et dans toutes
les directions.
Comment vont se recombiner toutes ces ondes réémises ? Avant de répondre nous
avons besoin de faire un petit détour par l'optique d'un miroir de télescope.
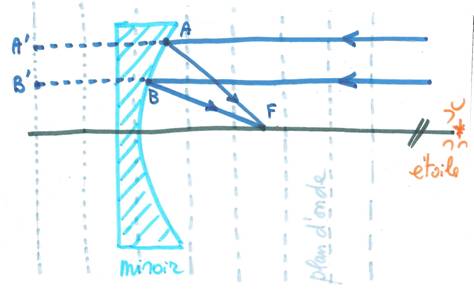
Sur la figure nous voyons les
plans d'égale phase qui arrivent sur le miroir. Quand l'onde plane se réfléchit
sur le miroir paraboloïdal, tous les rayons vont converger au foyer F. Il est
facile de voir qu'ils seront en phase, d'après la définition même d'une
parabole (lieu des points équidistants d'une droite et d'un point). En effet,
AF = A'A, BF = B'B etc. Or dans le plan contenant A'B' les rayons auraient tous
été en phase, comme avant. Donc, puisqu'ils ont parcouru le même chemin en
arrivant en F, ils sont en phase, comme avant.
Regardons ce qui se passe près du
foyer, quand l'image d'une étoile distante arrive sous forme d'une onde plane.
Tous les électrons excités, par l'onde et qui réémettent, donneront des ondes
qui seront toutes en phase en un seul point, le point F. En dehors il y aura
une superposition des ondes, mais elles seront un peu décalées (on dit
déphasées). Il y aura même des points où les ondes s'annuleront complètement.
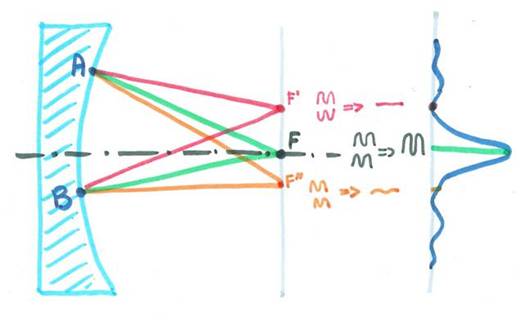
Si on considérait deux électrons
réémetteurs on observerait, comme pour les interférences de deux sources
synchrones, une série de maxima et de minima. Mais en prenant en compte tous
les électrons on observe un maximum en F (car il n'y a qu'en ce point que
toutes les ondes sont en phase) et quelques ondulations de part et d'autre du
maximum, résidus de la superposition de toutes les ondes déphasées. Le calcul
précis montrerait que l'image de l'étoile ponctuelle apparaîtrait comme sur la
figure ci-dessous. Cette figure s'appelle l'image de diffraction du miroir. On
l'appelle aussi "la tache d'Airy", du nom de l'astronome anglais qui
a contribué à faire comprendre ce phénomène. Sa demie largeur
est :
e =
1,22 l/D
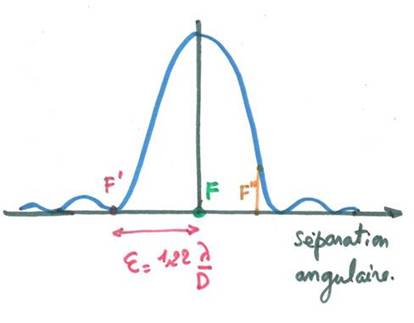
Si on applique cette relation à un
télescope dont le miroir a un diamètre D (en mètre) pour une longueur d'onde de
550 nanomètres, on trouve :
e =
1,22 . 550 . 10-9
/D
(e
est ici exprimé en radians).
Calculons le en seconde de d'angle.
e =
1,22 . 550 10-9 . (180 .
3600 / p)/D
C'est-à-dire :
e =
0,14 / D
(e
est exprimé en seconde d'angle et D en mètre).
On voit qu'avec un petit télescope
de 20 cm
de diamètre on peut séparer deux étoiles distantes angulairement de moins d'une
seconde d'angle. Nous verrons qu'en pratique, l'atmosphère vient perturber ce
résultat. Mais il y a des solutions avec les optiques modernes.
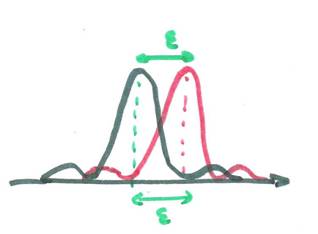
Que voit-on en pratique, quand on regarde une
étoile avec un télescope ? L'étoile est ponctuelle. On devrait donc voir une
"tache d'Airy". C'est-à-dire une image centrale de largeur e,
entourée d'anneaux de moins en moins brillants (les petites ondulations
résiduelles). En pratique, avec un gros télescope, la tache d'Airy est si
petite que les anneaux résiduels sont complètement masqués par les turbulences
atmosphériques. En revanche, avec un petit télescope les anneaux sont parfois
visibles.
DIFFRACTION
ET INTERFERENCES -Activités
G. Paturel et J. Ripert
Pour observer un phénomène
d'interférence, il suffit, à l'aide d'une aiguille, de percer deux tout petits trous, séparés d'un demi millimètre, dans du
papier d'aluminium. Pour cela, placer le papier d'aluminium sur du carton et
enfoncer seulement l'extrémité de l'aiguille. Placer les deux trous devant
l'œil et observer dans une obscurité partielle l'ampoule allumée d'une lampe de
poche placée à cinq ou six mètres. Il ne faut pas observer le réflecteur de la
lampe mais l'ampoule seule, en ouvrant le boîtier de la lampe.
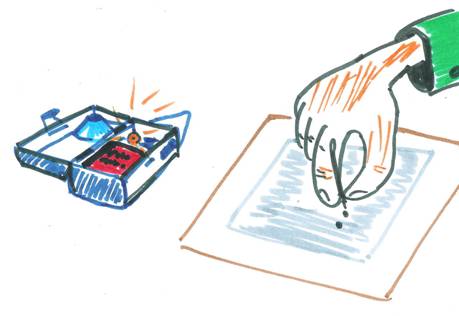
On voit l'ampoule striée de bandes
sombres et claires qui sont orientées perpendiculairement à la direction des
deux trous. Nous avons réussi à faire une ou deux photos du phénomène, mais la
réalité est bien plus belle. Essayez, c'est simple et ça marche.

Les
franges d'interférences

Pour observer un phénomène de
diffraction et une tache d'Airy, c'est un peu pareil. Il suffit, à l'aide d'une
aiguille, de percer un petit trou d'aiguille dans du papier d'aluminium. Avec
une aiguille très fine on peut percer au diamètre de l'aiguille. Le trou sera
ainsi bien rond et on pourra voir les anneaux de diffraction. Placer le trou
devant l'œil et observer. L'ampoule peut être un peu plus proche que
précédemment. Les anneaux ne sont pas très réguliers mais ça marche !
En tous cas, on voit bien que la
lumière se comporte de manière inhabituelle : elle ne va pas en ligne droite
bien sagement, sinon on verrait les bords du trou bien nets, ce qui n'est pas
le cas.

Une vilaine tache d'Airy.