RADIOACTIVITE : EXERCICES
EXERCICE 1 : Radioactivité
β- .
Le nucléide ![]() est radioactif (radioactivité β-).
Sa période (ou demi-vie) est 5500 ans.
est radioactif (radioactivité β-).
Sa période (ou demi-vie) est 5500 ans.
Ecrire l’équation de sa désintégration.
Soit un échantillon
contenant ce seul nucléide radioactif qui a une activité correspondant à 16
électrons émis par seconde. Au bout de combien de temps cette activité
sera-t-elle réduite à 4 électrons émis par seconde ?
SOLUTIONS
![]()
Activité divisée par 4 au bout de 2T = 11000 ans.
![]()
EXERCICE 2 : Décroissance
radioactive.
La période du![]() est
de 38 ans.
est
de 38 ans.
1° - Calculer la constante radioactive de ce nucléide.
2°- A partir de 1g de polonium, quelle est la masse restante
au bout de 1 jour, 1 an, 10 ans, 100 ans, 1 000 ans?
SOLUTIONS
1°.![]() .
.
2°. n = No.e-λt
ou m = mo. e-λt.
● t = 1 jour : ![]() .
.
● t = 1an : ![]()
● t = 10 ans : ![]()
● t = 100 ans :![]()
● t =1 000 ans : ![]()
![]()
EXERCICE 3 : Décroissance
radioactive.
Soit une source radioactive constituée par un milligramme de
radium dont la période (ou demi-vie) est voisine de 1 600 ans. Calculer la
masse de radium restant au bout de 1 an, 100ans, 1 000 ans, 10 000
ans, 100 000 ans.
SOLUTIONS
● ![]()
● Les masses cherchées sont respectivement (en mg) :
0,9996 ;
0,9957 ; 0,958 ; 0,65 ; 1,3.10-2 ; 1,5.10-19.
![]()
EXERCICE 4 : Décroissance
radioactive.
Le tritium ![]() se désintègre avec une constante
radioactive :
se désintègre avec une constante
radioactive :
λ =
1,789.10-9s -1.
a) Quelle est sa période radioactive. Donner le résultat en
années.
b) On considère une masse de tritium qui donne 2.106
désintégrations par seconde. Quelle est la valeur de cette masse ? (![]() ).
).
SOLUTIONS
a) ![]()
b) Le nombre de désintégration par seconde est aussi l’activité
de la source considérée :
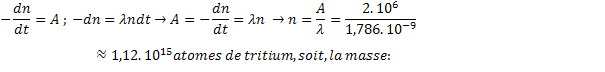
![]()
![]()
EXERCICE 5 : Radioactivité![]()
On rappelle que la radioactivité d’un sel de radium est due
à la destruction spontanée des atomes de radium et que, en moyenne, il se
détruit un atome sur 2 300 au cours d’une année.
A – Calculer le nombre des atomes détruits chaque seconde dans
une masse de radium de 10-9g.
Nombre d’Avogadro : N = 6,02.1023,
Ra = 226g.
B – A la suite de réactions nucléaires n’intervenant pas
ici, un atome de radium en se
détruisant donne naissance à quatre
particules![]() ,
de masse m et de charge q. Expérimentant sur 1g de radium, on constate que les
particules convenablement recueillies à un courant de 4,6.10-8A. En
déduire la charge q d’une particule
,
de masse m et de charge q. Expérimentant sur 1g de radium, on constate que les
particules convenablement recueillies à un courant de 4,6.10-8A. En
déduire la charge q d’une particule ![]() .
.
SOLUTION
A – Nombre d’atomes de radium dans 10-9g :
![]() .
.
En 1s, il se détruit
1 atome sur : n = 2 300.365,25.24.3 600.
Donc, ici le nombre d’atomes détruits en 1s est :
![]()
B – En 1s, le nombre des particules α émises est :
4.36,7.109≃ 1,47.1011
Si q est la charge d’une de ces particules, la charge totale
vaut 1,47.1011 q ou 4,6.10-8C ; d’où :
![]()
![]()
EXERCICE 6 : Radioactivité ![]() .
Scintillations sur une sphère
.
Scintillations sur une sphère
Par radioactivité ![]() ,
le radium
,
le radium ![]() se transforme en radon
se transforme en radon ![]() avec
émission d’une particule
avec
émission d’une particule ![]() .
.
1° - Calculer la charge q, la masse m et la charge massique
q/m de la particule á émise. On considérera que la masse du proton et celle du
neutron sont égales à 1u et on négligera la diminution de masse. On
donne : 1u = 1,66.10-27kg, charge du proton : e = 1,6.10-19C.
2° - On place un petit fragment de radium, de masse 3.10-5g
au centre d’une sphère de verre creuse, de rayon r = 0,12m, recouverte sur sa
paroi interne d’une pellicule de sulfure de zinc. Les particules ![]() sont
émises uniformément dans toutes les directions et, chaque fois que l’une
d’elles frappe l’écran au sulfure de zinc, une scintillation se produit. On
fait le vide dans la sphère et on dénombre 75 scintillations en 200s sur une
surface de 0,015 mm2 (observation avec un microscope). En déduire le
nombre moyen de particules
sont
émises uniformément dans toutes les directions et, chaque fois que l’une
d’elles frappe l’écran au sulfure de zinc, une scintillation se produit. On
fait le vide dans la sphère et on dénombre 75 scintillations en 200s sur une
surface de 0,015 mm2 (observation avec un microscope). En déduire le
nombre moyen de particules ![]() émises
par s et par g de Ra.
émises
par s et par g de Ra.
(Surface d’une sphère : S = 4𝜋R2)
3° - La vitesse d’émission des particules ![]() est 104km.s – 1.
Calculer en J et en MeV l’énergie cinétique d’une particule et l’énergie
libérée par s par la désintégration de la source de radium considérée.
est 104km.s – 1.
Calculer en J et en MeV l’énergie cinétique d’une particule et l’énergie
libérée par s par la désintégration de la source de radium considérée.
SOLUTION
1°
![]()
![]()
2° - Les particules ![]() sont émises uniformément dans toutes les
directions, donc le nombre de scintillations est proportionnel à la surface
considérée sur la sphère donc, en notant N le nombre total de désintégration,
on a (en 200 secondes) :
sont émises uniformément dans toutes les
directions, donc le nombre de scintillations est proportionnel à la surface
considérée sur la sphère donc, en notant N le nombre total de désintégration,
on a (en 200 secondes) :
N. à
S = 4𝜋r2 n = 75 à
s = 0,015mm2
![]()
D’où le nombre de désintégrations par s et par g de
Ra :
![]()
3° - La mécanique classique est utilisable :
![]()
Le nombre de désintégration par s est 4,525.106à
Energie libérée : w = 1,5.10-6J =
9,4.106MeV
![]()
EXERCICE 7 : Radioactivité![]()
Le plutonium ![]() est radioactif et émetteur
est radioactif et émetteur ![]() .
Sa période (demi-vie) est T ≃ 24 000ans.
.
Sa période (demi-vie) est T ≃ 24 000ans.
1° - Ecrire l’équation de la transformation radioactive.
2° - Calculer la masse d’uranium 235 et d’hélium formés au
bout de 10 ans à partir d’une masse de 10g de plutonium 239.
SOLUTION
1° - ![]()
2° - ● Nombre initial d’atomes de plutonium : ![]()
● Nombre d’atomes de plutonium au bout
de 10ans :
![]()
● Nombre d’atomes désintégrés en
10ans :
![]()
● Ce nombre est aussi le nombre
d’atomes d’uranium est d’hélium formés.
On en déduit :
- la masse d’uranium :
![]()
- la masse d’hélium : il se fait 1 atome d’hélium pour
1 atome d’uranium
![]()
![]()
EXERCICE 8 :
Désintégration de courte période
Le bismuth ![]() est
radioactif et émetteur
est
radioactif et émetteur ![]() .
.
1°- Ecrire l’équation
de désintégration. Quel est l’élément formé ?
Extrait du tableau périodique des éléments :
80Hg ;81Tl ; 82Pb ;
83Bi ; 84Po ; 85At ; 86Rn.
2° - Soit une source radioactive contenant initialement 0,1g
de bismuth radioactif. Grâce à un compteur, on a montré qu’il produit, à partir
de l’instant initial, 4,484.1019 désintégrations en 15 minutes.
Calculer la période radioactive (demi-vie) du ![]()
(Nombre d’Avogadro : N = 6,02.1023)
3° - Calculer le volume d’hélium produit en 30 minutes
(volume mesuré dans les conditions normales) par cette source radioactive.
SOLUTION
1° -![]()
2° - Cherchons le nombre d’atomes de bismuth 212 :
![]()
En 15min, le nombre de désintégration est 4,484.1019 (16% de N0),
la période radioactive est donc courte, de l’ordre du quart d’heure.
En t = 15min, le nombre n de désintégrations est :
![]()
![]()
3° - Au bout de 30min, le nombre des atomes de bismuth
restant est :
![]()
D’où le nombre de désintégrations qui est égal au nombre
d’atomes d’hélium produit :
![]()
On en déduit immédiatement
- le nombre de moles d’hélium :
![]()
- le volume d’hélium (1mole
à 22 400cm3)
v = 1,37.10-4.22 400 ≃
3,07cm3
![]()
EXERCICE 9 :
Datation par le carbone 14.
a) Dans la haute atmosphère, sous l’effet du bombardement
neutronique, l’azote ![]() se transforme en carbone
se transforme en carbone ![]() radioactif. La désintégration de ce carbone 14
donne de l’azote 14. Ecrire les équations de ces 2 réactions nucléaires.
radioactif. La désintégration de ce carbone 14
donne de l’azote 14. Ecrire les équations de ces 2 réactions nucléaires.
b) La période du carbone 14 est 5 590 années, il permet
d’effectuer des datations.
Un échantillon de charbon de bois, trouvé dans une grotte
préhistorique, donne 212 désintégrations par minute. Un échantillon de même
masse, préparé à partir d’un jeune bois,
donne 1 350 désintégrations par minute. Quel est l’âge de l’échantillon
des bois anciens ?
Indication :
Reportez – vous au paragraphe B – 2°) qui explique la datation par le carbone
14.
SOLUTION
1°- ![]()
![]()
2°- Activité : ![]()
● Bois jeune : n = N0à
A0 = λN0
● Bois ancien : ![]()
● ![]()
t≃
14 930 années