Exercice résolu sur les interférences
lumineuses
Source :http://www.chimix.com/ifrance/devoirs/t070.htm
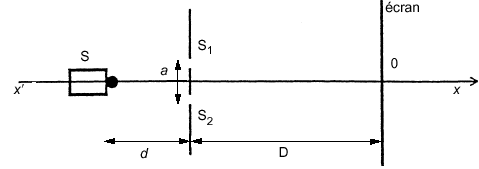
Le dispositif comprend une plaque percée de deux trous de Young
distants de a =500 µ m. En utilisant comme source émettrice S un laser He-Ne,
de longueur d’onde l=
633 nm on produit des interférences sur un écran. La plaque est placée à une
distance d =20 cm de la source, l’écran à une distance D = 4 m de la plaque. Les deux
trous de même diamètre sont placés à égale distance de la source et se
comportent comme deux sources synchrones et cohérentes.
1. Expliquer le phénomène d’interférences en
quelques lignes.
2. Au point O, la frange est-elle brillante
ou sombre ? Justifier.
3. Les franges brillantes sont équidistantes.
L’intervalle qui les sépare est appelé interfrange et noté i . On cherche à
connaître les paramètres dont peut dépendre i (nature de S, a , d , D) et à en
donner une expression parmi les propositions suivantes :
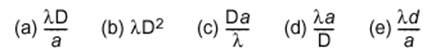
Par l’analyse
dimensionnelle, éliminer une ou plusieurs propositions.
4. En réalisant plusieurs expériences, où
l’on fait varier un seul paramètre en laissant les autres identiques, on
effectue les constatations suivantes :
-L’utilisation
d’un laser vert montre que l’interfrange diminue ;
-Si on
éloigne l’écran, l’interfrange augmente ;
- La
position de S sur l’axe ne modifie pas l’interfrange ;
- Les
deux trous étant rapprochés de l’axe, les franges s’écartent les unes des
autres.
En
utilisant ces résultats, trouver parmi les propositions (a), (b), (c), (d),
(e), l’expression de l’interfrange i , en justifiant le raisonnement.
Donner
la valeur de l’interfrange i obtenue avec le laser He-Ne.
CORRECTION
1-On observe un phénomène d ’interférences
lumineuses en tout point d ’un
écran où se superposent les 2 faisceaux lumineux issus des 2
sources secondaires S1 et S2.
Ces 2 faisceaux lumineux issus d’une même source ponctuelle S sont
cohérents.
Si les 2 vibrations qui interfèrent sont en phase, l’amplitude de
la vibration est maximale, les interférences sont dites constructives
et sur l’écran on a une raie brillante.
Si les 2 vibrations qui interfèrent sont en opposition de phase,
l’amplitude de la vibration est nulle, les interférences sont destructives et sur l’écran, on a une raie
sombre.
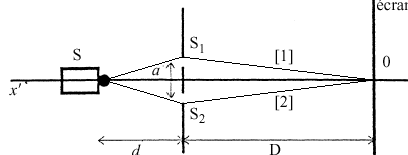
2-Pour atteindre le point O, les
vibrations lumineuses parcourent la même distance qu'elle prenne le chemin [1 ]
ou le chemin [2 ]. La différence de marche est nulle.
Les 2 vibrations qui interfèrent en O sont alors en phase :
frange brillante et interférences constructives.
3-analyse dimensionnelle
: voir point méthode
L'analyse dimensionnelle:pour vérifier l'homogénéité d'une
formule
l, D, a, d et i sont des longueurs :[L]
(a) lD/a
expression possible car [L] [L] [L]-1 = [L]
(b) lD²
expression impossible car [L] [L] [L] = [L]3
(c) Da / l
expression possible car [L] [L] [L]-1 = [L]
(d) la/D
expression possible car [L] [L] [L]-1 = [L]
(e) ld/a
expression possible car [L] [L] [L]-1 = [L]
4-recherche de la bonne expression de l'interfrange :
lvert < lrouge et
l'interfrange i diminue: i et l
varie donc dans le même sens.
(c) Da / l
éliminé.
D augmente, alors l'interfrange i augmente: D et i varie dans le
même sens.
(d) la/D
éliminé
la position de S sur l'axe xx' ne modifie pas l'interfrange: i
indépendant de d
(e) ld/a
éliminé
la distance S1S2 = a et l'interfrange i
varie en sens contraire
(a) lD/a
expression correcte.
calcul de l'interfrange :
l = 633
nm = 6,33 10-7 m
D= 4 m; a = 5 10-4 m
i = 6,33 10-7 *4 /5 10-4
= 5,06 mm.