LES FRANGES D’ YOUNG
Source :http://www.lac.u-psud.fr/experiences-optique/interferences/young/fr-young.html
Thomas Young (1773-1829)
était médecin physicien .Il est connu surtout pour la contribution qu’il
apporta sur la nature de la lumière. En 1803, il montre que si l’on éclaire un
écran à travers une fente étroite, il se forme des franges très lumineuses en
des points qui auraient dû rester dans l’ombre si la lumière s’était propagée
en ligne droite .
Plus étonnante encore l’expérience réalisée avec
une double fente montre que deux rayons lumineux peuvent se combiner pour
produire une alternance de bandes claires et noires. L’expérience conduit à se
paradoxe : lumière
issue de la 1ère fente + lumière issue de la 2ème fente = Zéro de lumière
Comment interpréter la
formation de ces bandes sombres ? Quel modèle pour la lumière permet
d’interpréter ce phénomène ?
1-L’expérience
d’Young :
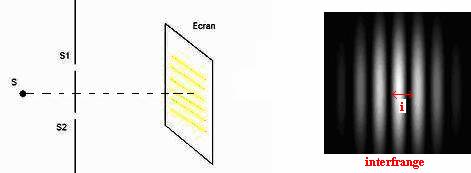
Dans l'expérience de Young, on utilise une source lumineuse S
monochromatique et on interpose une plaque percée de 2 fentes. Celles-ci se
comportent comme des sources secondaires S1 et S2.
On observe alors, sur un écran placé derrière, un réseau très serré de franges
alternativement sombres et claires parallèle aux fentes. La frange centrale
(observée sur la médiatrice se S1S2) est lumineuse.
Schéma de principe des
fentes de Young.
2-l’interprétation de Thomas Young :
a- Le caractère ondulatoire de la lumière
La théorie des interférences a été établie par analogie
avec les phénomènes observés à la surface de l’eau.
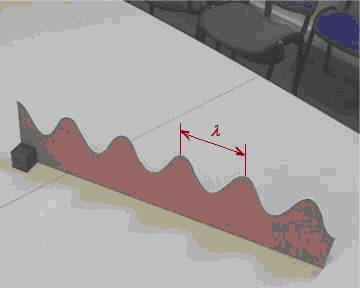
Rendons nous donc au bord d’un étang….
Le fait de jeter une pierre dans l’eau fait apparaître un système de
rides à profil sinusoïdal qui se déplace avec une vitesse V. Si un corps
flottant est placé sur le trajet, on voit le corps monter et descendre au
passage des vagues. Contrairement à une idée reçue, le corps ne se déplace pas,
il se contente d’osciller sur place.
Mathématiquement,
nous écrirons que le corps flottant reproduit le mouvement de la source un
instant plus tard.
Soit yS(t)=a cos ωt le mouvement de la source.
Si on appelle τ le temps que met le paquet de rides pour
atteindre l’objet flottant en M, le mouvement de celui-ci est décrit par l’expression :
yM(t)=yS(t-t)=a cos[ω(t - τ)] ou
l’expression entre crochet s’appelle la phase du mouvement. Celle-ci est
définie à 2P prés
A partir de cette équation, il y a trois
possibilités de raisonnement.
a- raisonnement sur les temps.
Avec ω = 2π / T, il vient a cos(ω t - 2π τ
/T). Par suite, si τ est égal à un nombre entier de périodes (τ
=kT), le mouvement du corps flottant est identique à celui de la source.
Tous deux passent par le maximum où le minimum en même temps.
b- raisonnement sur les phases.
Posons 2π τ /T = φ . Le mouvement du corps flottant est :
a cos (ω t - φ).
Si φ = 2 k π, les mouvements de la source et du corps flottant sont
dits «en phase». Maxima ou minima se produisent au même instant. Pour les
valeurs φ = (2k +1) π on parle d’opposition de phase. A
l’instant où la source est à son maximum d’amplitude, le corps flottant est à
la position la plus basse.
c- raisonnement sur les distances
Puisque les rides se déplacent à une vitesse constante V, le corps
flottant situé à une distance d est atteint au bout du temps τ = d /
V. L’équation devient a cos (ω t - 2π d / VT). V étant une
vitesse et T un temps, le produit VT est une longueur que l’on appelle longueur
d’onde et que l’on note λ.
L’équation du mouvement du corps flottant devient a cos (ωt -
2π d / λ). Par suite pour toutes les distances telles que d =
kλ ( k entier), le mouvement du corps est identique à celui de la source.
Il est en opposition pour les valeurs 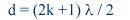
Note : A l’instant t = τ , prenons une photo du
système de rides. Le temps étant une fonction de la distance d. figé, ω τ = cste. Nous
visualisons ainsi l’équation a cos ( 2π d /λ + cste) qui devient
Deux points situés à des
distances différentes ont le même état vibratoire si l’argument du cosinus
diffère de 2kπ. Les points les plus proches ont lieu pour k=1
soit : (
2π d1
/λ + cste) = ( 2π d2 /λ + cste) + 2π . D’où l’on
tire d1 - d2 = λ .
La longueur d’onde n’est donc
autre que la distance entre deux rides successives.
On utilise parfois la grandeur inverse σ =1 /λ que
l’on appelle nombre d’onde. Elle correspond tout simplement au nombre de rides
présentes par unité de longueur. Ainsi pour l’eau, λ= 0,15 m d’où :
σ = 1/ 0,15 = 6, 67 m-1 . Il y a un peu moins de 7 rides sur une
distance de 1 mètre.
b-Expliquons le phénomène
d’interférences avec ce modèle :
Lâchons maintenant simultanément
deux pierres de façon que les équations de mouvement des sources s’écrivent a
cos ωt.
Si t1 et
t2 sont les temps mis par chaque
système de rides pour atteindre le corps flottant, le mouvement de celui-ci est
donné par l’équation :
S = a cosω (t + t1) + a cosω (t + t2) = 2a cosω [ t1 -t2) / 2] cosω [ t + (t1 + t2) / 2]
Le corps flottant oscille donc à
la même fréquence que les sources, avec un décalage qui dépend de la quantité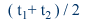 mais
aussi avec une amplitude qui vaut
mais
aussi avec une amplitude qui vaut 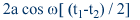
Or cette expression peut prendre
la valeur zéro en certains points du plan, ce qui se traduit par : Mouvement
dû à la source S1 + Mouvement dû à la source S2 = Absence
de Mouvement.
C’est sur cette simple
analogie que s’est appuyé FRESNEL pour développer la théorie ondulatoire de la
lumière.
De préférence à un calcul
mathématique, examinons ce qui se passe avec une maquette découpée dans une
simple planche d’isorel (photos :1,2,3et4)
1

2

3

4

Calcul de
l’interfrange i
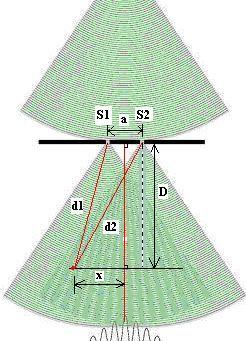
Revenons à l’optique.
Appelons D la distance de l’écran aux fentes et x la distance du point
d’observation à leur axe. La coutume veut que a désigne la distance entre les
fentes (ce qu’il ne faut pas confondre avec l’amplitude de l’oscillation).
|
|
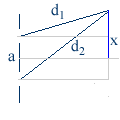
d1 et d2 étant les hypoténuses de triangles de
côtés D
et x ± a / 2, on a immédiatement
d1 - d2 =
que l'on peut écrire : 
|
a et x étant toujours beaucoup
plus petits que D (typiquement D > 1m, x = qqs cm et a < 1mm, les termes
littéraux sont << 1. Ce qui fait que les radicandes se mettent sous la
forme (1 + ε)1/2
dont le développement limité est 1 + ε /2.
D'où l'on tire : d1 - d2 = a x / D . Lorsqu'on fait varier x, la
quantité (d1 - d2) varie. Or, on passe d'un maximum au
suivant lorsque (d1 - d2) a
varié de λ. Désignons par i la variation correspondante de x. Il vient :
i = λ D /a
i est appelé interfrange.
Avec la simulation qui suit, vous
pouvez modifier les différents paramètres : l, D, a et vérifier si l’influence de chacun d’eux sur la valeur de
l’interfrange i correspond à l’expression ci-dessus.
Interférences mécaniques et lumineuses: animations
|
|
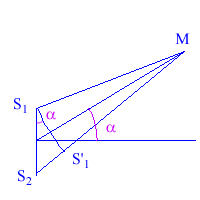
Note: Un autre manière de
faire le calcul de façon approchée consiste à tracer un arc de cercle centré
sur M et à assimiler la corde S1 S'1 à la perpendiculaire issue de S1 sur M S2.
De même, on suppose que la bissectrice de l’angle
S1 M S2 (qui est perpendiculaire à cette
corde) passe par le point situé à mi-distance des deux sources.
Avec ces approximations, on a :
tan α = x / D et sin α =
(d1 - d2 ) / a.
|
Pour les petits
angles tan α ≈ sin α ≈
α ce qui conduit au même résultat que précédemment. Mais
avec cette démonstration, la validité des approximations faites est beaucoup
plus délicate à établir.
Mesures de longueurs
d’onde
On oublie trop souvent que
cette expérience fut la première qui permit d’attribuer un nombre à une couleur
de l’arc-en ciel. Si, dès 1700, Newton avait inventé le prisme, l’avait
installé à la sortie de son télescope pour étudier la composition de la lumière
émise par les astres, ses descriptions manquaient de précision faute d’un
étalon de mesure.
Reprenons la valeur de
l’interfrange i = λ D / a. On voit que le facteur multiplicatif
(D/a) peut être énorme. Avec D = 4m et a = 0,5 mm, il vaut 8000. En utilisant un microscope
pour déterminer précisément la valeur de a, et en faisant porter les mesures
sur une vingtaine d’intervalles, on peut atteindre une précision de l’ordre de
1% sur la mesure de λ.
A la notion vague de couleur (jaune-vert, jaune paille, jaune franc,
jaune-or, jaune orange) se substituait un chiffre dont la précision allait
considérablement augmenter avec l’invention des réseaux de diffraction puis de
l’interféromètre de FABRY-PEROT.
La cohérence temporelle de
la lumière
L’observation des rides à la
surface de l’eau permet d’aller plus loin dans la compréhension du phénomène
lumineux. Lorsqu’on jette une pierre dans l’eau, il se forme seulement un
paquet de quelques rides. Supposons que nous lâchions les deux pierres à des
instants très différents. Le premier paquet s’est éloigné et le second ne
pourra le rattraper. Les interférences disparaissent.
Un siècle après l’expérience d’YOUNG, la théorie atomique allait
reprendre cette idée.
La lumière est émise par les atomes. Au repos ceux-ci n'émettent pas,
mais lors d’une collision, ils acquièrent de l’énergie qu’ils restituent sous
la forme de minuscules éclairs dont la durée peut varier de quelques
picosecondes (10-12 sec.) à rarement plus que quelques
microsecondes (10- 6 sec.).
De plus, contrairement aux rides qui conduisent à une oscillation
toujours perpendiculaire au plan de l’étang, l’oscillation de l’onde
électromagnétique se produit avec un azimut quelconque.
Or, l’expérience montre que les interférences
ne peuvent se produire que si les directions d’oscillation sont parallèles.
Ainsi la probabilité pour que deux atomes émettent simultanément
et, de plus, avec la même direction de polarisation est
infime.
FRESNEL avait énoncé la règle que l’on ne pouvait produire des
interférences avec deux sources différentes et qu’il fallait procéder en
divisant puis recombinant un même faisceau.
Nous traduisons ceci en écrivant que la lumière naturelle est
incohérente.