CORRECTION DES TROIS PREMIERS
EXERCICES SUR LA NATURE VIBRATOIRE DES SONS
Exercice I :
1°/ a) La nature du son est « Vibratoire »
b) Le son émis par cette source est « AUDIBLE » car les fréquences des
sons audibles sont comprises entre 20Hz et 20kHz,
et la fréquence du son émis par S1 est égale à 1230Hz.
2°/ Oui, le son se propage dans l’eau car l’eau est un milieu naturel et le son se propage
dans un milieu naturel
3°/ Calcul de la célérité de propagation du son émis par S1
dans l’air à 20°C
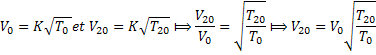
AN : 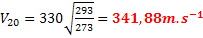
4°/ a) Calcul de la longueur d’onde du son émis par S1
dans l’air à la température 0°c :
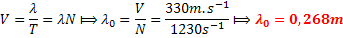
b) Calcul de la nouvelle température de l’air si cette
longueur d’onde vaut 𝜆1=
0,280m :
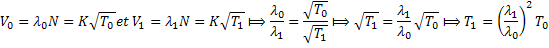
AN : 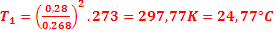
Exercice II :
1°/ Le son est produit par la
vibration d’objets
2 exemples d’émetteurs du son :
- un coup de bâton sur un tambour
- vibration d’une corde de guitare
2°/ Calcul de la célérité de propagation du son dans l’air à
30°C :
à 0°C , V0 =330m.s-1 ⟾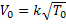
à 30°C , V30= ?
⟾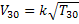
⟾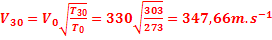
3°/
Calcul de la distance entre l’observateur et le lieu où la foudre est
tombée : d
à 0°C : V0=330m.s-1 et t = 13s la
durée entre le coup de tonnerre et l’éclair.
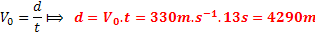
Exercice III :
1°/
Définitions de :
-Infra-sons:
sons inaudibles par l’oreille humaine, de fréquences inférieures à 20Hz
-Ultra-sons :
sons inaudibles par l’oreille humaine, de fréquences supérieures à 20kHz
-Sons audibles
par l’oreille humaine, de fréquences comprises entre 20Hz et 20kHz
2°/ La
vitesse de propagation du son dans l’air à 0°C est V=20,04√T.
a)
T représente la température absolue du milieu exprimée en Kelvin
(K)
b)
Calcul de la
vitesse de propagation du son dans l’air à 0°C=273K.
Soit
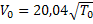 avec
T0=0°C=273K
avec
T0=0°C=273K
AN : 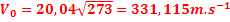
3°/ Un son
de fréquence 5000Hz se propage dans l’air.
a)
A la
température 27°C, la longueur d’onde 𝜆 :
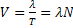 or N=5000Hz et t= 27°C= 300K ⟾
or N=5000Hz et t= 27°C= 300K ⟾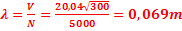
b)
Si la longueur
d’onde est de 8cm, calculons la température de l’air :
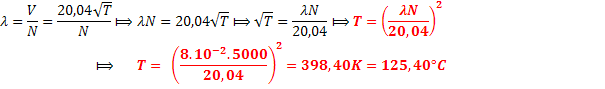
4°/Un son
de fréquence N1=2000Hz se propage dans l’air à la température 27°C
et un autre son de fréquence N2=2400Hz se propage dans l’air à la
température t2 et les 2 sons ont la même longueur d’onde ;
calculons t2 :