Phénomènes périodiques I

I-Un mobile est animé d’un mouvement rectiligne sinusoïdal, de fréquence N=50Hertz et d’amplitude a= 3mm, passe à l’instant initial à l’origine des abscisses en allant vers le sens négatif des élongations.

1°) a) Calculer : la pulsation ω et la phase initiale φ du mouvement.

      b) En déduire l’expression de l’élongation x en fonction du temps t ;

2°) Calculer les positions et les vitesses du mobile aux instants suivants : t₀=0s ; t₁=T/4 ; t₂=T/2 ; t₃= 3T/4 ; t₄=T où T est la période du mouvement.

3°) Tracer la courbe x= f(t) pour t Є[0,T]

II-Une corde élastique OA, de longueur L=1m, de masse m=50g, est tendue horizontalement par une force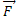, d’intensité F. L’extrémité O de la corde est animée d’un mouvement vibratoire transversal, de fréquence N=100Hz et d’amplitude a=2mm. On négligera la réflexion et l’amortissement des ondes le long de la corde.

1°)a) Calculer F si la célérité de propagation des ondes le long de la corde est V=10m.s^-1

     b) Définir est calculer la longueur d’onde λ de la vibration.

2°) Ecrire l’équation horaire du mouvement du point O, sachant qu’à l’instant t=0s, il passe par sa position d’équilibre en se déplaçant dans le sens positif des élongations.

3°) a) Ecrire l’équation horaire du mouvement d’un point M de la corde tel que OM=15cm.

      b) Comparer les mouvements de O et de M.

4°) Représenter l’aspect de la corde à l’instant t= 5.10^-2s.

III- Une lame vibrante munie d’une pointe P détermine en un point O de la surface libre d’un liquide au repos, une perturbation transversale sinusoïdale, d’équation horaire y₀(t)= 4sin (200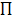t), (y₀ en cm et en s).

1°)a) Qu’observe-t-on à la surface libre du liquide ?

     b) Qu’appelle-t-on perturbation transversale ?

2°) Calculer la longueur d’onde λ sachant que le mouvement se propage à la célérité V=10m.s^-1

3°) Ecrire l’équation horaire du mouvement d’un point M de la surface libre du liquide, tel que OM =x=25cm.

4°) Représenter l’aspect de la surface libre du liquide à l’instant t=0,03s.

IV- L’extrémité O d’une longue corde vibrante horizontalement tendue est animée d’un mouvement vibratoire sinusoïdal, transversal, d’équation horaire : y₀(t)=4.10^-3sin 200∏t  (avec y₀ en mètres et t en secondes)

La célérité des ondes le long de la corde est v= 20ms^-1.

On néglige l’amortissement et la réflexion des ondes sur la corde.

1°)a) Déterminer la fréquence de mouvement de O.

     b) Calculer la longueur d’onde λ.

2°) Ecrire l’équation horaire du mouvement d’un point M de la corde tel que OM= x

Application numérique :x=25cm

3°) Soit P un point de la corde, tel que OP= 55cm. Déterminer :

  a)Le nombre des points de la corde, entre O et P, qui vibrent en opposition de phase avec le point O.

  b) La position de ces points par rapport au point O.

4°)a) Ecrire l’équation cartésienne de la corde représentant l’aspect de la corde à l’instant t= 3,5.10^-2s.

     b) Représenter l’aspect de la corde à cet instant.

V- Le mouvement d’un point A situé à l’extrémité d’une lame d’acier disposée horizontalement est un mouvement rectiligne sinusoïdal vertical d’amplitude a=4mm et de fréquence f= 10Hz.

1°) Ecrire l’équation horaire du mouvement y_A(t) du point A, le milieu O de la trajectoire est l’origine des élongations et à t=0, A passe par le point O en se dirigeant dans le sens descendant choisi comme le sens négatif.

2°)a) Tracer le vecteur de Fresnel représentant la fonction y_A(t) et tracer la courbe représentant y_A(t).

Echelle : abscisse : 12cm représente une période temporelle

              Ordonnée :2cm représente une élongation de 4mm

     b) Déterminer l’instant où A passe pour la seconde fois par le point B d’élongation y_B=2mm, à l’aide de la courbe précédente et par le calcul.

3°) On attache en A une corde horizontalement tendue et infiniment longue. La célérité de propagation des ondes le long de la corde est 40m.s^-1.

    a)Déterminer : -la longueur d’onde λ.

                            -l’élongation yM(t) d’un point M de la corde tel que AM=20cm

    b) Calculer y_M à l’instant t= 2,5.10^-2s

VI-1°) L’extrémité O d’une lame vibrante est animée d’un mouvement sinusoïdal d’amplitude a et de fréquence N= 50Hz. Le mouvement de O débute à l’instant t=0s de sa position d’équilibre en allant dans le sens positif des élongations, avec une vitesse v₀=0,628m.s^-1.

    a)Vérifier que l’amplitude du mouvement de O est a=2mm.

   b) Ecrire l’équation du mouvement de O

2°) Le point O de la lame précédente est relié à l’une des extrémités d’une corde élastique de masse par unité de longueur μ=20g.m^-1.La corde est tendue horizontalement par une force d’intensité  F= 2N. On néglige la réflexion et l’amortissement des ondes dans le milieu élastique.

a)   Calculer la célérité de propagation V des ondes le long de la corde.

b)   Définir et calculer la longueur d’onde λ de la vibration

c)   Soit un point M de la corde tel que OM=60cm.

Déterminer, entre O et M, le nombre des points de la corde vibrant en opposition de phase avec le point O

3°) Représenter l’aspect de la corde à l’instant t=5.10-2s

On donne : ∏=3,14

VII-  Soit une fonction sinusoïdale d’équation : y₀(t)= 2sin(200∏t+∏) (en mm)

1°)a) Déterminer l’amplitude, la pulsation, la période, la fréquence et la phase initiale de y₀(t)

     b) Représenter y₀ par un vecteur de Fresnel.

2°) Soit y₁(t)= 3 sin(200∏t-∏/2) (en mm)

a)   Calculer le déphasage entre y0 et y1.

b)   Comparer y₀ et y₁.

c)   Calculer le décalage horaire du couple (y₀, y₁)

3°) Déterminer la fonction d’onde résultante y= y₀+y₁ en utilisant la méthode de construction de Fresnel et puis par calcul.