PHYSIQUE TA

2013-2014

PHENOMENES PERIODIQUES

Exercice 1

Soient deux fonctions sinusoïdales définies par : y₁(t) = 2 sin (100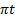 + ) ; y₂(t) = 3 sin (100 + )      

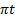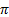 t en seconde et y en cm

1.      Calculer y₁(0) ; y₂(0) ; y₁(0,005) ; y₂(0,005)

2.      Préciser l’amplitude, la période, la fréquence et la phase initiale de chaque fonction sinusoïdale.

3.      Déterminer la phase du mouvement de :

a.      Y₁ à l’instant t = 0s

b.     Y₂ à l’instant t = 0,01s

4.      Comparer les deux fonctions sinusoïdales.

Exercice 2

La vibration de l’extrémité d’une lame vibrante a pour élongation :

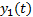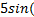 = 20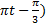 ; t en seconde et y en cm.

1.       Calculer les élongations aux instants suivants : t = 0,05s ; t = 0,025s et  t = 0s.

2.       Représenter le vecteur de Fresnel associé à y₁(t).

3.       Calculer la longueur du segment décrit par y₁.

4.       Donner la fonction y₂(t) caractérisée par les conditions suivantes :

­         Son amplitude est  le double de celle de y₁.

­         y₁ et y₂ sont synchrones

­         y₂ est en quadrature retard par rapport à y₁.

Exercice 3

L’extrémité A d’une corde élastique est animée d’un mouvement vibratoire sinusoïdale dont l’élongation, exprimée en cm, est donnée par la fonction définie par y_A(t) = 4sin20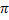t ; y en cm et t en seconde

1.       Déterminer l’amplitude, la phase initiale, la fréquence et la période du mouvement de A.

2.       Le mouvement vibratoire se propage le long de la corde avec une vitesse de 2,5ms^-1. Définir et calculer la longueur d’onde.

3.       Quelle est l’équation du mouvement d’un point M situé à 62,5cm de l’extrémité A.

4.       Calculer en radian la différence de phases correspondant aux mouvements de deux points M et M’ séparés par une distance de 40cm.

Exercice 4

Un point S est animé d’un mouvement vibratoire sinusoïdal. Sa trajectoire est un segment de droite de 20mm de longueur et il se trouve à l’instant t = 0s à son élongation maximale positive. Sachant qu’il effectue 100 vibrations en 2 secondes :

1.       Définir et calculer la période du mouvement vibratoire.

2.       Ecrire l’équation horaire de son mouvement.

3.       Donner l’expression de la vitesse de S en fonction du temps t. En déduire la vitesse de S à t = 0s.

4.       Représenter la courbe de diagramme de mouvement de S dans l’intervalle [0 ; 2T].

On prendra l’échelle 1cm pour 0,01s.

Exercice 5

L’extrémité O d’une longue corde élastique est animée d’un mouvement sinusoïdal de fréquence 50Hz et d’amplitude 2cm. La célérité de propagation des ondes le long de la corde est 20ms^-1 et il n’y a pas de réflexion des ondes sur l’extrémité de la corde.

1.       Donner l’équation horaire du mouvement de O sachant qu’à l’instant t = 0s, O passe par sa position d’équilibre en allant dans le sens des élongations négatives.

2.       Déterminer la vitesse du mouvement de O à l’instant t = 0,01s.

3.       Etablir l’équation horaire y_M(t) du mouvement du point M de la corde tel que OM = x. Application numérique :   x = 20cm. Comparer les mouvements de O et M.

4.       a) Ecrire l’équation cartésienne représentant l’aspect de la corde à l’instant t = 0,045s.

       b) Représenter graphiquement l’aspect de la corde à cet instant.

Exercice 6

L’extrémité O d’une corde élastique est attachée à un vibreur animé d’un mouvement vibratoire transversal de fréquence 50Hz et d’amplitude 2mm. Sachant qu’à t = 0, O passe par sa position d’équilibre dans le sens positif des élongations. Le front d’onde de la corde parcourt une distance d = 0,7m
pendant une durée 7.10^-2s.

1.       Ecrire l’équation horaire du mouvement de O.

2.       Calculer la vitesse de propagation du mouvement le long de la corde.

3.       Définir et calculer la longueur d’onde.

4.       Ecrire l’équation horaire du mouvement d’un point M de la corde tel que OM = x. A.N. : x= OM = 25cm.

5.      Représenter la courbe du diagramme du mouvement de M en fonction du temps et dans
l’intervalle [0 ; 0,04s]

Exercice 7

Soit une corde élastique de longueur l = 64cm et de masse m = 20g. De son extrémité S se propage
un mouvement d’équation : Y_s(t) = 4.10^-2sin(200pt +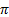)  ; t en s et y_S en m.

1.       Préciser l’amplitude, la période, la fréquence et la phase initiale de S.

2.       Calculer la tension de la corde.

3.       Définir et calculer la longueur d’onde.

4.       Etablir l’équation horaire du mouvement d’un point M de la corde tel que SM = x. application numérique x = 25cm.

5.       Représenter graphiquement le diagramme du mouvement de M dans l’intervalle [0 ; 2,25T]

Exercice 8

Une lame vibrante munie d’une pointe S, frappe la surface libre d’un liquide au repos. Elle est animée d’un mouvement sinusoïdal de fréquence N = 100Hz et d’amplitude a = 3mm. Au cours de la propagation des ondes, on négligera l’amortissement et la réflexion.

1.      a) Qu’observe-t-on sur la surface libre du liquide ?

  b) Ecrire l’équation horaire du mouvement du point S sachant qu’à l’instant t = 0s, S passe par sa position d’équilibre en allant dans le sens négatif des élongations.

2.      La distance entre deux crêtes consécutives est de 4mm. En déduire la longueur d’onde 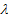 et calculer la célérité de propagation des ondes.

3.      Ecrire l’équation horaire du mouvement d’un point M de la surface libre du liquide situé à la distance x du point S. A.N : x = 16mm. Comparer les mouvements de S et M.

4.      Représenter l’aspect de la surface libre du liquide à t = 4.10^-2s.

5.      Déterminer le nombre des points qui vibrent en phase avec le point S à l’instant t = 4.10^-2s.

Exercice 9

Une lame vibrante provoque à l’extrémité S d’une corde élastique, de longueur l = 2m et de masse m = 40g, un mouvement vibratoire sinusoïdal qui se propage le long de la corde. La corde est tendue horizontalement par une force d’intensité F = 0,5N. On néglige l’amortissement et la réflexion des ondes aux extrémités de la corde.

1.      Calculer la célérité de propagation des ondes le long de la corde.

2.      La courbe suivante représente la variation de l’élongation y_s en fonction du temps t.

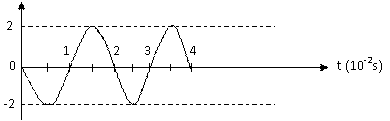
a) Déduire de cette courbe les valeurs de la période et de la fréquence du mouvement de S.

b) Ecrire l’équation horaire du mouvement S en fonction du temps t

3.       Donner l’expression de la vitesse de S en fonction du temps t. En déduire la vitesse maximale de S.

4.      Définir et calculer la longueur d’onde.

5.      Ecrire l’équation horaire du mouvement d’un point M de la corde tel que SM = x. application numérique x = SM = 7,5cm. Comparer les mouvements de S et de M.

6.      Tracer la courbe de diagramme du mouvement de M dans l’intervalle [0 ; 6.10^-2s]