Corrections avec rappel du sujet :

sujet1  sujet2

Auteur : Mme RASOLOARIMANA Vololoniarivo, professeur de sciences physiques au collège RASALAMA-Antananarivo

Sujet 1 :

Deux points S1 et S2 sont animés de mouvements sinusoïdaux d’équation horaire :

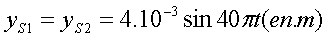
S₁ et S₂ sont en contact avec la surface de l’eau et sont distants de 7,5cm

1-     Qu’observe-t-on à la surface de l’eau ?

On observe des rides fixes en formes d’hyperboles de foyers S₁ et S₂ appelées franges d’interférences.

2-     Les ondes se propagent à la surface de l’eau à la célérité v=0,4m.s-1. Calculer :

  a -La longueur d’onde l.

           b-L’amplitude du mouvement d’un point M sachant que d₁=S₁M=11.5cm et d₂=S₂M=12cm.

        Quel est l’état vibratoire de M ?

a- La pulsation w=40.p=2.p.N  et donc la fréquence N=20Hz, d’où la longueur d’onde :

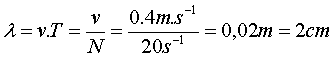
b-

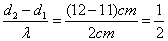
Les deux ondes se croisent en M avec un décalage spatial d’une demi longueur d’onde, ce qui signifie qu’elles sont en opposition de phase en ce point. L’interférence des deux ondes est destructive et M est immobile (si l’on suppose que les amplitudes de chaque onde sont restées constantes).

3-

         a- Déterminer le nombre de points immobiles sur le segment S₁S₂.

        b- En déduire leur distance par rapport à S1.

On a en ces points la double condition :

(1)  d₂-d₁=(2k+1)l/2=2k+1(cm)

(k est ici un entier positif, nul, ou négatif)

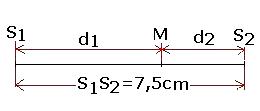
(2)  d₂ +d₁=S₁S₂=7,5cm

Eliminons d₂ entre les deux équations précédentes, il vient :

2d₁=7,5-2k-1=6.5-2k

 d₁=3,25-k (avec d₁ en cm)

Sachant que:0<d₁<7,5cm

On obtient les 8 valeurs suivantes (voir tableau ci-dessous) :

Remarque : ces valeurs sont les coordonnées des intersections des franges d’interférence (hyperboliques) avec la lignes des sources S₁S₂.

Sujet 2

A l’extrémité de l’une des branches d’un diapason, vibrant à la fréquence N =100Hz, est fixée une tige munie d’une fourchette dont les deux pointes sont distantes de d=2cm. Elles frappent la surface d’une nappe d’eau en deux points O₁ et O₂ où elles créent des vibrations sinusoïdales  de même amplitude  a=1mm, se propageant sur la surface de l’eau à la célérité v=40 cm.s-1. Dans cet exercice, on négligera l’amortissement.

1-

a-Quel phénomène se produit-il à la surface de l’eau ?

b-Décrire les observations et les expliquer.

a- C’est  le phénomène d’interférences mécaniques.

b- On observe des rides fixes en formes d’hyperboles de foyers O₁ et O₂ appelées franges d’interférences.

2-

a-Ecrire les équations horaires des mouvements de O₁ et O₂ sachant qu’à l’instant t=0s, les deux points O₁ et O₂ passent par leur position  d’équilibre respective en se déplaçant dans le sens positif.

2-a Les deux points effectuent des oscillations de même amplitude a, même fréquence N (et donc de même pulsation w), et en phase.

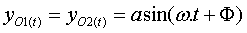
La phase F dépend des conditions initiales.

A t=0, les points passent par leur position d’équilibre et donc y_O1=y_O2=a. sinF =0; 2 solutions sont alors  possibles :F=0 et F=P .

Les points se déplacent dans le sens positif et donc à cet instant la fonction y est croissante, y’(t=0)=a.w.cosF>0, par conséquent la seule solution est F=0.

 L’équation s’écrit donc:

.

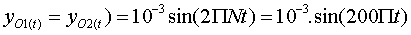b-Ecrire l’équation horaire du mouvement d’un M de la surface de l’eau tel que O₁M=d₁=1,2cmet d₂=O₂M=2cm.

La perturbation en M a la date t produite par l’onde provenant de O₁ et qui a parcouru la distance d₁ s’écrit:

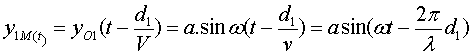
La perturbation en M a la date t produite par l’onde provenant de O₂ et qui a parcouru la distance d₂ s’écrit:

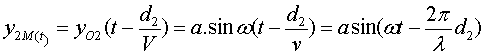
La perturbation résultante en M est la somme des perturbations précédentes

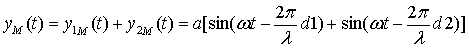
utilisons la relation trigonométrique:

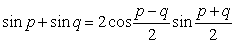
Il vient :

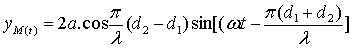
La longueur d’onde est : l=v/N=40cm.s^-1/100s^-1=0.4cm

Le calcul du terme d’amplitude donne:

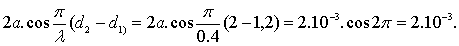
Il est maximum, ce qui signifie que les ondes interfèrent de manière constructive en M.

Le terme de phase :

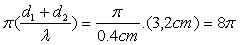
Et finalement :

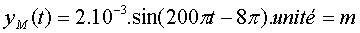
3-Déterminer le nombre de points immobiles sur la segment O₁O₂  et leur positions respectives par rapport à O₁.

On a en ces points la double condition :

(1)  d₂-d₁=(2k+1)0.4/2=0,4k+0,2(cm)

(k est ici un entier positif, nul, ou négatif)

(2)  d₂ +d₁=S₁S₂=2cm

Eliminons d₂ entre (1) et (2) :

-2d₁=0.4k+0.2-2

d₁=-0,2k+0.9

avec 0<d₁<2cm

Suivant les valeurs de k on obtient 10 valeurs de d₁: