FONCTIONS_EXERCICES

Exercice 1

Pour chacune des fonctions f,

· déterminer l'ensemble de définition D.

· étudier la parité

· calculer les limites aux bornes de D.

· calculer f'(x) et étudier son signe.

· dresser le tableau de variations de f.

· préciser les points en lesquels la courbe admet des tangentes parallèles à l'axe des abscisses.

· construire la courbe de f.

a) f(x)= x²-2x ; b) f(x)=-x²+2 ; c) f(x)=-x³ +1 ; d) f(x)=2x³-6x+1

Exercice 2

Pour chacune des fonctions f,

· déterminer l'ensemble de définition D.

· étudier la parité

· calculer les limites aux bornes de D. En déduire les équations des asymptotes s'il en existe.

· calculer f'(x) et étudier son signe.

· dresser le tableau de variations de f.

· préciser les points en lesquels la courbe admet des tangentes parallèles à l'axe des abscisses.

· construire la courbe de f.

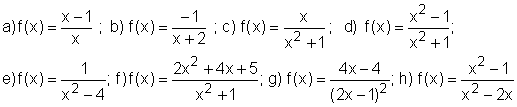
Exercice 3

Soit f la fonction définie par . On note C la courbe représentative de f dans un repère orthonormé

1.- Déterminer les réels a, b et c sachant que la courbe C admet l'axe des abscisses comme asymptote et passe par les points A(1,0) et (.

Dans la suite du problème, on prend a = 0, b = 1 et c = -1, donc .

2.- Déterminer l'ensemble de définition D de f.

3.- Calculer les limites de f aux bornes de D. En déduire les équations des asymptotes à la courbe C.

4.- Calculer f '(x) et étudier son signe.

5.- Dresser le tableau de variation de f.

6.- Montrer que le point I ( 1 ; 0 ) est un centre de symétrie.

7.-Donner l'équation de la droite T tangente à C au point d'abscisse x₀ = 1

8.- Construire T et C

Exercice 4

On considère la fonction f définie par . On note C la courbe représentative de f .

1.- Déterminer l'ensemble de définition D de f.

2.- Calculer les limites aux bornes de D; En déduire les équations des asymptotes horizontale et verticales.

3.- Calculer f '(x) et étudier son signe. Dresser le tableau de variation de f.

4.- Déterminer le point d'intersection de C avec l'axe des abscisses.

5.- La droite d'équation x =1 est-elle un axe de symétrie?

6.- Tracer C et T dans un même repère.

Exercice 5

Une entreprise fabrique chaque jour x objets. Le coût de fabrication de ces x objets exprimé en francs,est donné par . (On admet que x)

1.- Calculer le coût de fabrication de 40 objets.

2.- Le prix de vente d’un objet est de 34 F. Soit g(x) le bénéfice réalisé pour x objets vendus.

a) Calculer le bénéfice réalisé par l’entreprise pour 40 objets vendus.

b) Montrer que

c) Calculer g’(x), étudier son signe et dresser son tableau de variation. (On ne demande pas de construire la courbe de f)

En déduire la valeur de x pour laquelle l’entreprise réalise le bénéfice maximal.

Exercice 8

On dispose d’une feuille de carton rectangulaire, de 80 cm de long et de 50 cm de large, avec laquelle on veut fabriquer une boîte ayant la forme d’un parallélépipède rectangle.

Pour cela, on découpe dans la feuille quatre carrés égaux de côté x aux quatre coins (figure 1), puis on plie le carton suivant les segments [AB], [BC], [CD] et [DA]. On obtient alors la boîte (figure 2).

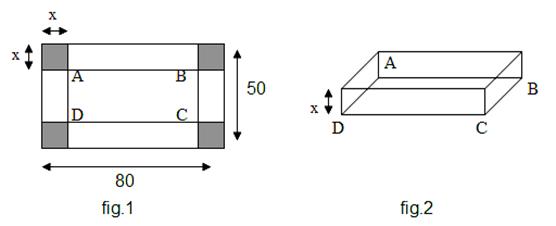
1.- Préciser dans quel intervalle I peut varier x pour que la boîte soit réalisable.

2.- Montrer que le volume de la boîte (en cm³) s’écrit en fonction de x :

.

3.- Etudier les variations de V sur l’intervalle [0 ; 25 ] et en déduire la valeur de x pour laquelle le volume V est maximal. Quel est alors le volume de la boîte obtenue ?

Exercice 9

On donne le tableau de variations d'une fonction f.

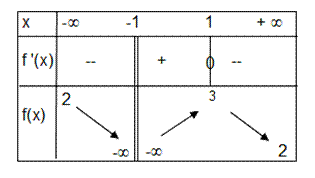
1.- Par lecture de ce tableau, déterminer :

a) l'ensemble de définition D de f.

b) les limites de f aux bornes de D

c) les équations des asymptotes

d) le point en lequel on a une tangente horizontale.

2.- Sachant que , construire la courbe représentative de f.