Le caractère relatif du temps

 

I- Une expérience troublante :

Bruno Rossi et David B.Hall de l'Université de Chicago ont réalisé une  expérience en 1941 .Ils ont mesuré le flux des muons (alors appelés « mésotrons ») au sommet du Mont Washington dans le New Hampshire aux Etats-Unis, à environ 2000 m d'altitude ainsi qu'à la base de la montagne.

Les muons sont des particules créés dans l’atmosphère à la suite de collisions de rayons cosmiques avec les molécules de l’atmosphère. Leur vitesse moyenne est 0,999c soit très proche de la vitesse de la lumière.

La durée de vie du muon est très courte, c'est une particule instable. Elle vit 1.5   microsecondes environ, après quoi elle se désintègre.

Cette particule se déplaçant à la vitesse de la lumière ne devrait parcourir, selon Newton, que : 300000 x 1.5x10^-6 = 0.45 km = 450 mètres durant sa courte vie.

Or ce n'est pas du tout ce que les physiciens  observent dans la réalité. La particule est tout à fait détectable au niveau de la mer soit 2000m plus bas!

Les particules semblent avoir une durée de vie beaucoup plus grande par rapport à un observateur terrestre lorsque celles-ci se déplacent  à grande vitesse par rapport à ce même observateur!

L’application du principe de la relativité énoncé par Einstein en 1905 doit permettre d’élucider ce phénomène qui semble troublant à première vue.  

 

II- L’hypothèse d’Einstein : l’invariance de la célérité de la lumière et la relativité du temps:

 

Pour illustrer cette hypothèse, reprenons l’expérience de Galilée sur la chute d’un objet du haut du mat d’un navire en mouvement rectiligne et uniforme. Celle-ci avait pour but d’illustrer le principe de la relativité de Galilée pour la mécanique.

 

Mais cette fois imaginons que l’objet est  un « grain de lumière », un « photon »  sans masse donc et se déplaçant à la vitesse de la lumière.

 

Avec un photon l’expérience est totalement irréalisable en pratique, car les durées de parcours et les distances sont infimes. C’est une expérience dite de « pensée »ou de « réflexion ». Le but de celle-ci est d’introduire un raisonnement  et d’apporter une conclusion  selon les hypothèses de départ. Ce type de raisonnement était souvent utilisé par Einstein lui-même pour faire comprendre sa théorie.

 

Cette « expérience » met en scène deux personnages : « monsieur MOB » qui est le passager d’un bateau en mouvement rectiligne et uniforme de vitesse V. Il est placé au pied du mât et regarde la photon descendre depuis le haut vers le bas. Quant à « monsieur FIX »  il se repose sur une ile et regarde passer le bateau,  il observe lui aussi le mouvement du photon.

Le bateau constitue le référentiel « mobile » (R’), l’ile ou la terre est le  référentiel « fixe » (R). (Les repères  sont « mobile» et « fixe » par rapport à un autre repère de référence qu’il est inutile de préciser pour notre raisonnement).

 

 

 

 

 

 

 

 

1- Description « Newtonienne » du mouvement du photon dans les deux référentiels R et R’:

 

 

 

 

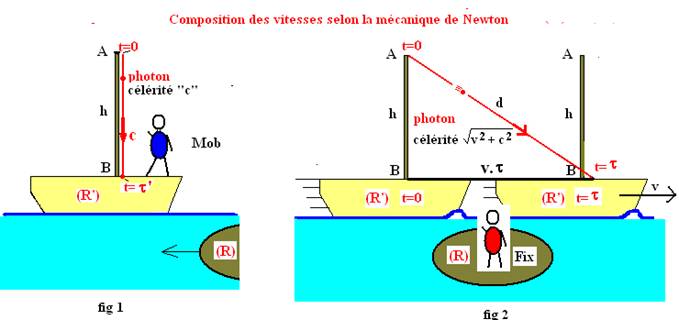
Nous considérons ici le photon comme un objet « classique » « tombant » du haut du mat. (sauf qu’un photon ne tombe pas car il est sans masse !). Il n’est donc soumis a aucune force, son mouvement est rectiligne et uniforme dans les deux repères…  

 

Durée du parcours du photon dans (R’) :

Pour MOB, le photon quitte le point  A à t=0 et arrive au pied du mat en B à t= t’ avec

t’=h/c

Durée du parcours du photon dans (R ) :

Pour Fix, le photon quitte le haut du mat à t=0 et arrive au pied du mat à t=t.

Pendant la chute, le bateau avance d’une distance : V.t.

La distance parcourue par le photon d est donc plus grande que précédemment :

Vitesse u du photon dans ( R )

Pour FIX, la vitesse c se compose vectoriellement  avec la vitesse V du bateau .Son module est :

 

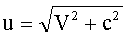
Finalement , la durée du parcours est:

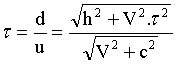
Elevons au carré cette expression :

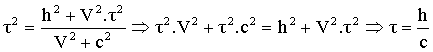
Et par conséquent,

 

t=t’

 

Nous constatons l’égalité entre t et t’, la durée du phénomène est donc la même dans les deux référentiels.  Une horloge mesurant la durée de chute dans le bateau en mouvement donnerait le même résultat qu’une horloge  restée à Terre.

 

Car si la distance augmente, la vitesse augmente dans les mêmes proportions, ce résultat « classique » n’est donc pas très surprenant.

 

 Conclusion selon cette étude : la vitesse du photon est différente selon le référentiel R ou R’ (elle est donc relative) mais la durée du phénomène est la même.

En mécanique newtonienne, la vitesse est relative au référentiel par contre le temps a un caractère absolu, indépendant du référentiel.

 

2- Description du phénomène en appliquant le principe de la relativité restreinte (2):

(2) la relativité est dite restreinte car elle considère des référentiels en mouvements rectiligne et uniforme donc « galiléens »

 

Enoncé du principe : la célérité de la lumière est invariablement égale à c (valeur proche de 3.10⁸m.s^-1) par rapport à n’importe quel référentiel galiléen.

 

Concrètement, si une source de lumière est en mouvement rectiligne et uniforme de vitesse V par rapport à un référentiel (R), la célérité de la lumière produite par cette source est « c »par rapport au référentiel (R’) de la source en mouvement.

Le principe de relativité stipule  que la lumière se déplace encore  à  la vitesse c  par rapport à (R) et non c+ V (si la source se déplace dans le même sens que la lumière) ou c-V (si la source se déplace dans le sens contraire) comme le suggère la loi de composition des vitesses de la mécanique de Newton.  La célérité de la lumière est indépendante de la source qui l’émet.

 

 

 

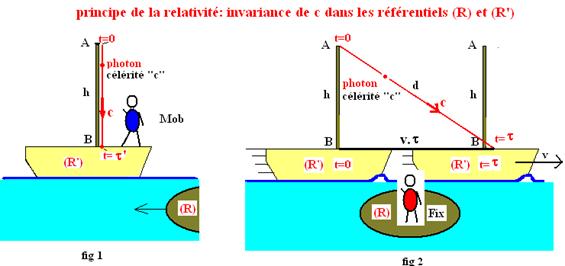
Reprenons les descriptions du mouvement du photon dans les deux référentiels

 

Durée du parcours du photon dans (R’) :

Pour MOB, le photon quitte le point  A à t=0 et arrive au pied du mat en B à t= t’ La durée du mouvement est toujours :  

t’=h/c

 

Durée du parcours du photon dans (R) :

Pour Fix, le photon quitte le haut du mat à t=0 et arrive au pied du mat à t=t.

Pendant la chute, le bateau avance d’une distance : V.t.

La distance parcourue par le photon d est toujours:

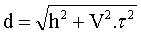
Selon le principe de la relativité, la vitesse du photon est indépendante de la vitesse du bateau et sa valeur est c :

 

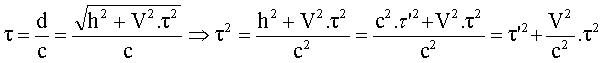
Soit :

 

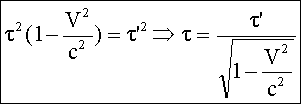
Conséquence :

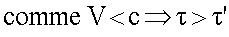
Par rapport à R, le photon parcours une distance plus grande mais à la même vitesse c, il est logique alors de penser que la durée du mouvement  est plus grande.

 

Supposons que les durées t et t’aient été mesurées par MOB et FIX chacun dans leur référentiel respectif avec une horloge. L’horloge de FIX mesure une durée plus grande pour le même phénomène observé, tout se passe comme si son horloge retarde par rapport à celle de MOB.

 

La durée est relative au référentiel dans lequel on effectue la mesure.  

 

III Interprétation de l’observation faite avec les muons :

 

La durée de vie t’ dans le référentiel R’ du muon est appelée « durée de vie propre ».

Pour un observateur terrestre, celle-ci  devient :

 

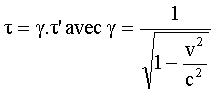
avec V=0.999c, g  estproche de 20 et donc : t=20.t’=20.1,6=32 microsecondes.

Cette durée mesurée dans un autre référentiel que le référentiel du muon est souvent qualifiée de « durée impropre ».

 

 

 

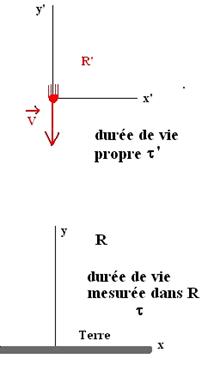
Pour un observateur terrestre, le muon doit  parcourir :

D=t.V=32.10^-6.3.10⁸=9600m

 

Le flux de muons est donc parfaitement détectable au niveau de la mer.

 

 

Nous proposons ci-après une application plus concrète présentée sous la forme d’exercices qui doivent  nous faire comprendre que les conséquences de  la relativité sont une réalité de tous les jours que nous le voulions ou pas !

 

IV « Sans la relativité pas de GPS »… mais pourquoi ?

Exercice  proposé par Tristan Rondepierre de l’Académie de Lyon

 

1 -Compétences exigibles :

 

Il faut connaître :

- le postulat de la relativité restreinte sur  la vitesse de la lumière dans le vide énoncé en 1905 par Einstein  et  la conséquence de ce postulat sur le caractère relatif du temps.

 

- les notions de « durée propre » et de « durée impropre » entre deux événements » suivant le référentiel de mesure 

 

- la relation entre les deux durées appelée « relation de dilatation des durées » ou  « relation donnant le ralentissement des horloges en mouvement »

 

 

2-Objectif  du contenu 

 

- Montrer une application concrète faisant intervenir la relativité  (restreinte et générale) : le GPS 

 

3-Description sommaire du G.P.S :

 

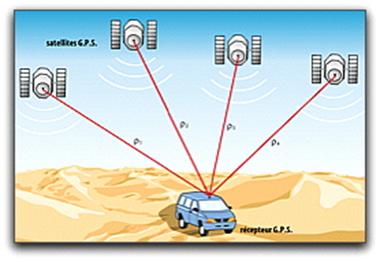
Le système de positionnement GPS (Global Positioning System) repose sur un principe que l’on peut résumer ainsi :

 

 

 

 

 

 

 

 

 

 

 

 

 

4 -Répondre aux questions et effectuer les calculs nécessaires:

a-Estimer un ordre de grandeur de la précision avec laquelle un GPS permet de se localiser.

 

b- Le mouvement du satellite n’étant pas rectiligne, on admettra que le temps propre est défini par l’horloge embarquée à bord du satellite. 

Expliquer qualitativement comment la relativité prévoit que l’horloge atomique embarquée à bord du GPS retarde par rapport à la même horloge restée au sol.

 

c- Calculer le retard t accumulé en une journée terrestre par l’horloge embarquée à cause de l’effet relativiste évoqué à la question précédente.

 

 

d-Calculer l’erreur Dd faite par le récepteur GPS s’il calcule la distance qui le sépare du satellite sans tenir compte du retard pris par son horloge au bout d’une journée. À votre avis, peut-on considérer Dd comme « négligeable » ?

 

e-Einstein a publié, en 1915, la relativité générale. Cette théorie, comme son nom l’indique, généralise la relativité restreinte à toutes les situations. En particulier cette théorie montre que le champ de pesanteur terrestre est lui aussi responsable d’un décalage entre l’horloge embarquée et celle restée au sol. Ce décalage est contraire à celui dû à la vitesse du satellite (calculé en (c)). On montre que le champ de pesanteur terrestre est responsable chaque jour d’une avance de 45 µs de l’horloge embarquée par rapport à celle restée au sol.

 

En tenant compte des deux effets relativistes, calculer le décalage temporel total T entre les deux horloges accumulé en une journée. En déduire l’erreur Dd_tot commise  par le récepteur GPS s’il ne tient pas compte des effets relativistes. Montrer que ce calcul justifie la nécessité de prendre en compte la relativité pour concevoir un récepteur GPS.

 

 

 

5-Réponses aux questions :

 

a-À partir de vos connaissances courantes sur le GPS, indiquer un ordre de grandeur de la précision avec laquelle un GPS permet de se localiser.

Un GPS embarqué en voiture permet de déterminer une position à la rue près : cela montre qu’il nous localise à moins de 10 m près.

 

b- On considère que le temps propre est défini par l’horloge embarquée à bord du satellite. 

Expliquer qualitativement comment la relativité prévoit que l’horloge atomique embarquée à bord du GPS retarde par rapport à la même horloge restée au sol.

Considérons deux événements localisés en un même point du satellite, séparés par une durée propre de valeur Dt_p, mesurée par l’horloge embarquée. Cela peut être par exemple l’intervalle de temps entre deux  flashs lumineux successifs émis par une même source lumineuse placée à bord du satellite.

 

La durée entre ces deux flashs  mesurée par une horloge liée au sol terrestre vaut :

 

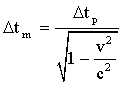
Soit :

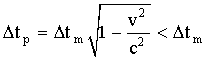
La durée propre Dtp mesurée par l’horloge embarquée est donc plus faible .Celle-ci retarde par rapport à celle restée au sol.

 

c-Calculer le retard t accumulé en une journée terrestre par l’horloge embarquée à cause de l’effet relativiste évoqué à la question précédente.

®    t est la différence entre Dt_p et Dt_m, soit :

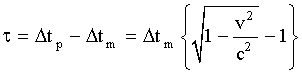
AN :

-      Dt_m est donc dans ce cas égal à la durée du jour terrestre : 24 × 3600 = 86 400 s.

-      v est la vitesse du satellite par rapport au sol :

v   = 1,4 × 10⁴ km·s^-1

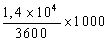= = 3,9 × 10³ m·s-¹

D’où :

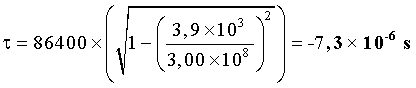
L’horloge embarquée retarde de 7,3 µs par jour.

 

 

 

 

d-Calculer l’erreur Dd faite par le récepteur GPS s’il calcule la distance qui le sépare du satellite sans tenir compte du retard pris par son horloge au bout d’une journée. À votre avis, peut-on considérer Dd comme « négligeable » ?

®  L’erreur commise par le récepteur s’il ne tient pas compte de la dilatation des durées est la distance parcourue par le signal pendant 7,3 µs. Or les signaux sont de nature électromagnétique, donc se propagent avec la même célérité que la lumière dans le vide.

L’erreur de distance vaut donc :

Dd = |ct| = 3,00 × 10⁸ × 7,3 × 10^-6 = 2,2 × 10³ m.

L’erreur commise si on ne tient pas compte des effets relativistes est donc de plus de 2 km ! Or comme nous l’avons indiqué en (b), la précision du GPS est de quelques mètres : on ne peut donc en aucun cas négliger Dd.

 

e-En tenant compte des deux effets relativistes, calculer le décalage temporel total T entre les deux horloges accumulé en une journée. En déduire l’erreur Dd_tot commise  par le récepteur GPS s’il ne tient pas compte des effets relativistes. Montrer que ce calcul justifie la nécessité de prendre en compte la relativité pour concevoir un récepteur GPS.

®    Le décalage temporel entre les deux horloges, vaut, au total :

T = 45 – 7,3 = 38 µs

L’erreur totale commise sur un calcul de distance vaut donc :

Dd_tot = |cT| = 3,00 × 10⁸ × 38 × 10^‒6 = 1,1 × 10⁴ m = 11 km

11 km est une erreur colossale, vu la précision attendue d’un GPS (à peine quelques mètres, comme nous l’avons indiqué en (a)). Ceci confirme que les corrections relativistes sont indispensables à la réalisation du système GPS.

 

 

En résumé, pour se positionner, le récepteur GPS évalue en même temps les distances par rapport à lui de plusieurs  satellites émetteurs. Ces distances sont calculées à partir des durées de propagation des  signaux provenant des satellites.  La moindre incertitude dt de mesure du temps de propagation de ces signaux entrainerait une incertitude c.dt beaucoup trop grande sur la localisation du récepteur (car c=3.10⁸m/s !) Les durées mesurées doivent donc être d’une précision phénoménale que seules les horloges atomiques peuvent donner. Le système GPS  a pu voir le jour après la mise au point de ces dernières technologies embarquées dans les satellites. D’autre part, comme nous l’avons vu, une correction de la durée est nécessaire pour tenir compte des effets relativistes dus à la vitesse du satellite et à la variation du champ de gravitation. C’est pour cela qu’une horloge atomique terrestre effectue en permanence la synchronisation des horloges des satellites. La connaissance de la relativité permet d’effectuer cette correction.

V Le  « Red shift » et  l’ expansion de l'univers

En observant des objets astronomiques lointains (galaxies ...), on recueille les spectres électromagnétiques de ces sources de lumière. L'absorption ou l'émission spectrale est souvent bien connue : on reconnaît facilement les spectres des éléments chimiques tels que :hydrogène, hélium, sodium ... qu'on a préalablement observés en laboratoire.

Si on remarque que les raies (d'absorption ou d'émission) sont décalées par rapport à leurs emplacements attendus, on peut en déduire que la source se déplace. Si le décalage observé est vers le bleu, la source se rapproche.

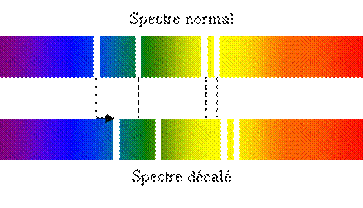
Pour la plupart des galaxies, on observe un décalage vers le rouge : le Red shift.(voir figure ci-dessus)

 

On interprète alors ce résultat par le fait que les galaxie s'éloignent les unes des autres. Par conséquent, on suppose que l'univers est en expansion.

Imaginons les galaxies comme des points sur un ballon gonflable. En le gonflant, les points s'éloignent. L'univers est donc en expansion.

La mesure du décalage vers le rouge permet d’en déduire la vitesse d’éloignement de l’étoile.

 

La lumière provenant d’une source  qui s’éloigne de la terre  a une longueur d’onde mesurée l  dans le référentiel terrestre .Elle s’exprime en fonction de la longueur d’onde propre l ' (dans le référentiel de la source)  et la vitesse d’éloignement v par la relation :

 

 

 

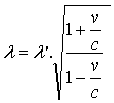
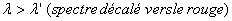
  Cette relation découle aussi du principe de la relativité énoncé plus haut.