LE DISPOSITIF SOLIDE-RESSORT

Source :http://pagesperso-orange.fr/physique.chimie

Cette leçon comporte cinq paragraphes.

1- FORCE DE RAPPEL EXERCEE PAR UN RESSORT

Un ressort exerce sur un solide une force de rappel F proportionnelle à son allongement : L – L₀ :

F = K ½L – L₀½ (1)

K est le coefficient de raideur du ressort. On l'exprime en N / m.

2- PENDULE ELASTIQUE LIBRE NON AMORTI

Un oscillateur élastique est constitué d'un ressort fixé à l'une de ses extrémités, l'autre extrémité est reliée à un solide. En l'absence de frottement solide-solide, ou solide-fluide, on dit que ce pendule élastique est non amorti. Etudions les oscillations horizontales du solide de masse m lorsque, après l'avoir écarté de sa position de repos, on l'abandonne à lui-même. On suppose que le ressort de coefficient de raideur K a une masse négligeable.

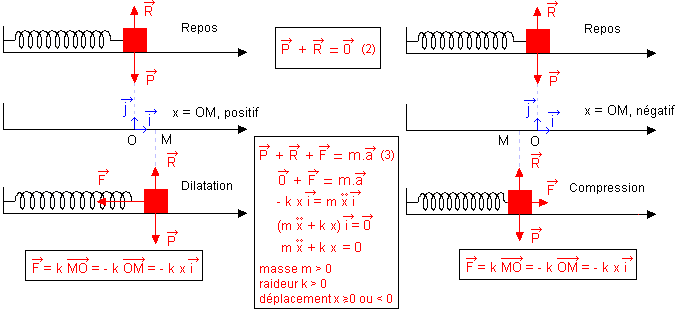
· Référentiel Galiléen : le solide Terre.

Repère orthonormé associé à ce référentiel : O, .

· Système étudié : le solide de masse m.

· Le solide est soumis à 3 forces :

: essentiellement action gravitationnelle de la Terre sur le solide (poids du solide).

: action normale de la piste sur le solide. Ici, on néglige les frottements.

: action du ressort sur le solide.

Remarque : La force exercée par le ressort sur le mobile peut s'écrire = K = - K (4)

Les coordonnées de dans la base sont :

Fx = - K x (5) Fy = 0 (6)

· Appliquons la deuxième loi de Newton (Théorème du centre d'inertie) :

Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse du solide par l'accélération de son centre d'inertie :

(7)

Ici, ce théorème s'écrit :

+ + = m (8)

· Projetons sur le vecteur unitaire :

0 + 0 - K x = m

m + K x = 0(9)

(10)

L'équation (10) est une équation différentielle du second ordre, à coefficients constants, sans second membre.

· Montrons que l'expression suivante (11), dans laquelle To représente la période propre du pendule élastique, est solution de l'équation différentielle du mouvement (10).

- Calculons la vitesse :

(12)

- Calculons l'accélération :

(13)

- Formons

(14)

- Cette expression (14) est bien identique à = 0 (10) à condition de poser :

(15)

CONSEIL ! Consulter le document :

L'analyse dimensionnelle: pour vérifier l'homogénéité d'une formule

· Conclusion du paragraphe :

La solution de l'équation différentielle du mouvement = 0 (10) est :

(11)

La période propre est :

(16)

Conclusion : Les oscillations libres d'un pendule élastique non amorti sont donc sinusoïdales.

La fréquence propre des oscillations est fo = 1 / To.

3- ENERGIE POTENTIELLE ELASTIQUE DU RESSORT. ENERGIE MECANIQUE DE L'OSCILLATEUR

· On montre que l’énergie potentielle élastique du ressort est :

E_P = ½ K (OM)² (17)

· L’énergie mécanique du système masse-ressort est :

E_m = E_C + E_P = ½ m V² + ½ Kx² (18)

· L’énergie mécanique du système masse-ressort se conserve en l’absence defrottement.

Remarque : On peut retrouver l’équation différentielle du mouvement = 0 (10) en écrivant que l’énergie mécanique du système masse-ressort se conserve. A faire.

4- OSCILLATEUR LIBRE AMORTI PAR FROTTEMENT VISQUEUX

- En présence de frottement solide-solide, ou solide-fluide, on dit que le pendule élastique est amorti.

- Dans le cas de frottement d'un fluide avec le solide (frottement visqueux), la force de frottement est proportionnelle à la vitesse (si celle-ci reste relativement faible). On écrit :

= - l avec l > 0 (19)

- Plaçons le dispositif solide-ressort dans un liquide.

La force de frottement, opposée au vecteur vitesse, est résistante.

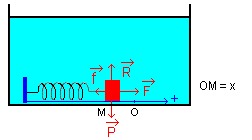
- Le solide est alors soumis à 5 forces (sur le schéma représente deux forces) :

: essentiellement action gravitationnelle de la Terre sur le solide (poids du solide).

: somme de la poussée d'Archimède et de l'action normale du support sur le solide.

: action du ressort sur le solide (force de rappel).

: force de frottement exercée par l'eau sur le solide

- La deuxième loi de Newton (Théorème du centre d'inertie) s'écrit :

+++ = m (20)

+- K - l = m (21)

- Projetons sur un axe horizontal :

0 + 0 - K x - l = m

m + l + K x = 0 (22)

- La solution mathématique de cette équation est hors programme. Donnons graphiquement les résultats à retenir :

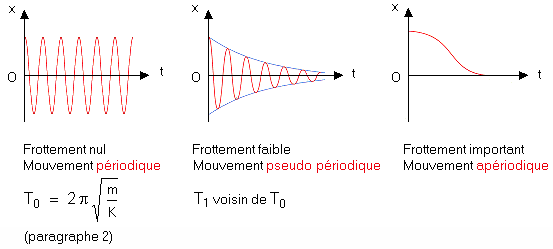
- En présence de frottement modéré (pendule placé dans un liquide peu visqueux comme l'eau) l’amplitude des oscillations diminue progressivement (régime pseudo périodique).

- Si les frottements sont très importants (liquide très visqueux), le pendule, écarté de sa position d'équilibre puis abandonné à lui-même, revient vers cette position d'équilibre sans osciller (régime apériodique).

Remarque :

- En présence de frottement, l'énergie mécanique du système solide-ressort ne se conserve plus. Elle diminue et se transforme en chaleur dissipée vers le milieu extérieur.

- Oscillations entretenues : Malgré les frottements on peut maintenir une amplitude constante à condition de prévoir un dispositif d'entretien des oscillations. Ce dispositif doit fournir au pendule une énergie permettant de compenser l'énergie dissipée par les forces de frottement. Cet apport d'énergie doit se faire à la fréquence où se produiraient les oscillations si le pendule n'était ni amorti, ni entretenu. Cette fréquence est la fréquence propre du pendule élastique.

5- OSCILLATIONS FORCEES D'UN PENDULE ELASTIQUE.

 5-1 Définition

Un oscillateur, de fréquence propre f_o = 1 / T_o, subit des oscillations forcées s'il oscille à une fréquence f imposée par un appareil extérieur appelée excitateur.

5-2 Etude expérimentale

· Le résonateur étudié est le pendule élastique représenté sur le schéma ci-dessous.

· Grâce à un moteur, on applique au pendule élastique, amorti par frottement solide-liquide, une force motrice extérieure, de période T pouvant être différente de la période propre de l'oscillateur.

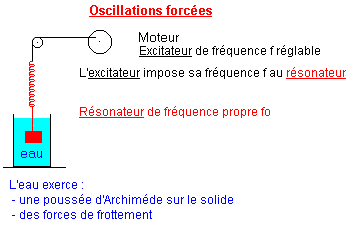
L'excitateur (moteur), de fréquence réglable, impose sa fréquence f au résonateur. Il agit, par l'intermédiaire d'une poulie et d'un fil sur l'extrémité haute du ressort.

- Changeons la fréquence f de l'excitateur et mesurons l'amplitude des oscillations du résonateur.

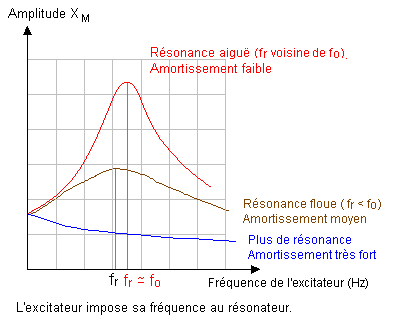
L'amplitude du résonateur passe par un maximum pour une fréquence particulière f_r imposée par l'excitateur (fréquence de résonance).

Cette fréquence de résonance f_r est proche de la fréquence propre f_o du résonateur si l'amortissement est faible.

La courbe donnant les variations de l'amplitude des oscillations du résonateur en fonction de la fréquence qui lui est imposée par l'excitateur s'appelle courbe de résonance.

Influence de l'amortissement : Si l'amortissement augmente (en plaçant le solide du résonateur dans des liquides de plus en plus visqueux) la fréquence de résonance diminue et la résonance devient plus floue. Il n'y aurait plus de résonance si l'amortissement devenait très important.