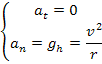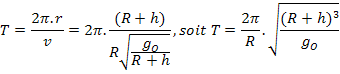MOUVEMENT DES SATTELITES

ENONCE

1- Le tableau ci-contre comporte des données relatives à deux type de satellites artificiels de la Terre en rotation uniforme dans le référentiel géocentrique.

a) L’une de ces satellites est dit géostationnaire. Indiquer lequel et justifier la réponse.

b) L’autre satellite est appelé satellite à « défilement» ; il évolue dans le plan contenant l'axe des pôles. Donner une explication de ce terme.

	METEOSAT	SPOT
Date de lancement	1977 1981	1986 1990
Altitude (km)	35 800	832
Période (min)	1 436	102
Champ d’observation au sol	Quasiment la moitié de la surface terrestre	Carré de 3 600 km²

Connaissant l'altitude de chacun de ces satellites, on se propose de vérifier par le calcul leur période révolution.

- La valeur du champ de pesanteur (attraction terrestre) à l'altitude h est donnée par ,avec go: intensité de la pesanteur au sol et R: rayon de la Terre.

a) En appliquant la deuxième loi de Newton au mouvement circulaire uniforme du satellite, déterminer l'expression de la vitesse de chaque satellite.

b) Définir la période de révolution de chaque satellite et donner son expression en fonction de go, R et h .

c) Calculer les périodes des deux satellites connaissant leurs altitudes.

Données : R=6380km et go= 9,8m.s^-2.

CONSEILS

On doit connaître l’ordre de grandeur de l’altitude d’un satellite géostationnaire (environ 36 000 km).

Comparer cette période à celles données dans le tablea ; elle doit correspondre à un jour, période d’un satellite géostationnaire.

Savoir qu’un satellite à défilement n’est pas fixe par rapport à la Terre. Sa période est différente de celle de rotation propre de la Terre.

Projeter la relation de la dynamique dans le repère de Frenet et utiliser les expressions des deux composantes de l’accélération.

Utiliser la donnée du texte exprimant gh.

Utiliser la définition de la période en fonction de la vitesse linéaire.

Convertir les distances en mètre et regrouper les termes constants utiles dans les deux applications afin de ne les calculer qu’une fois.

SOLUTION

1) a- Le satellite METEOSTAT Placé en orbite autour de la Terre à 36 000km d’altitude, est géostationnaire.

En effet, sa période donnée dans le tableau ci-dessus est égale au jour sidéral :

T = 1436 x 60 = 86 160s.

b) Dans le référentiel terrestre, le plan de la trajectoire de ce satellite n’est pas fixe, mais tourne autour de l’axe des pôles. Ce satellite « balaie » la surface de la Terre.

$Description : C:\Users\LAETITIA EDUCMAD\Documents\ANNEE 2013\DOCUMENTS MEDIATHEQUE 2013\M.RIVO\livre scaner\Nouveau dossier\Scan0026.jpg$

2) a- Théorème du centre d’inertie :

Soit

Soit, dans le repère de Frenet :

A l’altitude h, r = R + h, alors :

b) Par définition,

c) A.N : T = 86 200s, soit 1 437 min pour METEOSAT.

T = 6 090s, soit 102 min pour SPOT.

CONNAISSANCES
ESSENTIELLES DU COURS

1 A1 Accélération d'un satellite

1) Donner l'expression de la valeur de l'accélération d'un satellite terrestre en fonction de G, r et M_T.

2) Préciser la signification de chaque lettre.

3) Le vecteur accélération est-il centripète ou centrifuge?

2 A1 Satellite en orbite circulaire

On considère un satellite terrestre en orbite circulaire.

1) Le vecteur vitesse du satellite est-il constant?

2) La valeur de la vitesse est-elle constante?

3) Le mouvement du satellite est-il uniforme?

3 A1 Satellite géostationnaire

Afin de préciser le mouvement d'un satellite géostationnaire, répondre aux questions suivantes:

1) La période de rotation de la Terre autour de l'axe de ses pôles est 1 jour sidéral, soit 86 164 s. Dans quel référentiel cette période de rotation est-elle mesurée?

2) a) Dans quel référentielle satellite géostationnaire est-il immobile?

b) Quelle est sa période de rotation dans le référentiel géocentrique?

3) La trajectoire du satellite géostationnaire. dans le repère géocentrique, peut-elle être dans un plan :

a) méridien passant par l'axe des pôles?

b) passant par l'équateur?

c) contenant Paris?

4) L'altitude d'un tel satellite est-elle environ égale à:
360 km ? 3 600 km ? 36 000 km ?

5) Donner une utilisation des satellites géostationnaires.

4 A 1 Mouvement des planètes du système solaire

1) Dans quel référentielles trajectoires des planètes snt-elles approximativement circulaires?

2) Donner l'expression littérale de la troisième loi de Kepler et préciser les termes.

3) Les satellites d'une planète obéissent-ils à la troisième loi de Kepler?

4) a) Les trajectoires des planètes dans le référentiel héliocentrique sont-elles planes?

b) Qu ' est-ce que l'écliptique?

c) Le centre du Soleil se trouve-t-il hors du plan de l'écliptique?

APPLICATIONS
DIRECTES DU COURS

Altitude, période et vitesse d'un satellite (Ex. 5 à 7)
Données utiles-pour les exercices de 5 à 8 :

vitesse du satellite:

avec G = 6,67.10-¹¹ N. m²• kg-², go = 9,80 m.s^-1et R_T= 6380km.

5 A2 Le satellite EXPLORER avait une trajectoire circulaire à une altitude de 180 km. Calculer sa vitesse et période de révolution.

6 A2 Un satellite, placé sur une orbite circulaire dans le plan équatorial de la Terre, a une période de 7,82 h par rapport au référentiel géocentrique.

1) Calculer l'altitude de ce satellite.

2) Déterminer la masse de la Terre.

7 A2 MÉTÉOSAT est un satellite météorologique géostationnaire.

1) a) Définir le terme « géostationnaire ».
b) Préciser le plan de l'orbite.

2) Quelle est la période de révolution de ce satellite par rapport au référentiel géocentrique?

Donnée: période de rotation propre de la Terre: T=86164s.

3) À quelle altitude MÉTÉOSAT est-il placé?

8 A2 Satellite à trajectoire circulaire

La Terre est supposée sphérique, de rayon R_T et de masse M_T. La répartition des masses est de symétrie sphérique. Le champ gravitationnel terrestre, à l'altitude h

a pour expression , où G est a constante de gravitation universelle.
Donnée: M_T = 5,98.1024 kg.

1) Établir l'expression de la valeur du champ gravitationnel g à l'altitude h en fonction de h, R_T et go.

2) On considère un satellite artificiel de la Terre décrivant une trajectoire circulaire de centre 0, à l'altitude h = 350 km.

a) Nommer le référentiel d'étude du mouvement du satellite.

b) Donner l'expression du vecteur accélération du satellite

c)Justifier le fait que le mouvement est uniforme.

d) Calculer la vitesse du satellite et calculer sa période.

géos-

9 Satellite SPOT

Le 22 février 1986, la fusée ARIANE 3 plaçait sur une orbite circulaire, à l'altitude de 832 km, un satellite du programme SPOT (satellite spécialisé dans l'observation de la terre et dans la télédétection).

G étant la constante de gravitation universelle, la valeur du champ gravitationnel pour des points d'altitude h par
à la Terre est donnée par la relation:

11 Mouvement de la planète Mars

Dans le référentiel héliocentrique, la planète Mars décrit une orbite quasi circulaire autour du centre d'inertie du Soleil de rayon r.

1 Définir le référentiel héliocentrique.

M_T est la masse de la Terre et R_T le rayon de la Terre sphérique et homogène.

1- Déterminer l'expression de g en fonction de R_T, h et gO (valeur du champ gravitationnel au sol).

2- Un satellite artificiel de masse m décrit autour de la Terre une orbite circulaire de rayon r = R_T + h , où h représente l'altitude du satellite par rapport à la Terre.

a) Montrer que le mouvement circulaire du satellite est uniforme

b) Déterminer l'expression de la vitesse v du satellite sur son orbite en fonction de g_o, R_T et h. Calculer sa valeur pour le satellite SPOT.

c) Définir la période de révolution T du satellite. Déterminer son expression en fonction de g_o, R_T et h. Calculter la valeur en seconde, puis en heure et minute.

Données: go=9,80m.s^-2 et R_T=6,38.10³km.

10 la lune, un satellite naturel

La Lune et la Terre sont considérées comme des solides répartitions sphérique de masse, respectivement de centre C et O.
Le centre de la Lune décrit une trajectoire quasi circulaire de rayon r dans le référentiel géocentrique.

Données: go=9,8m.s^-2et R_T=6380km.

Exprimer la valeur du champ gravitationnel terrestre au centre de la Lune, en fonction de go, R_T et r = OC.

2) Appliquer le théorème du centre d'inertie à la Lune, dans le référentiel géocentrique, pour exprimer l'accélération du centre d'inertie de la Lune.

3) Déterminer, en fonction de go, R_T et r, la vitesse et période de révolution.

4) La période de révolution de la Lune dans le référentiel géocentrique est 27 j 7 h 44 min. Calculer la distance Terre- Lune.

2) Exprimer le champ de gravitation dû au Soleil au centre d'inertie de Mars. Préciser l'hypothèse envisagée pour exprimer ce champ de gravitation.

3) Dans le référentiel héliocentrique, exprimer l'accélération du centre d'inertie de Mars en fonction de r, M_S et G.

4) En déduire la période de révolution de Mars. Calculer numériquement cette période.

Données: le rayon de la trajectoire r = 227,94.10⁶ km, la masse du Soleil M_S = 1,98 . 10³⁰ kg et la constante de gravitation G = 6,67.10¹¹S.I.

1 2 A2 Détermination de la masse d'une planète
Lorsqu'un satellite est animé d'un mouvement circulaire autour d'une planète, le rayon r de son orbite et la période T de son mouvement vérifient la loi de Kepler:

1) Les satellites géostationnaires de la Terre ont une orbite circulaire de rayon G = 42 164 km et une période T_G= 86 164 s. Calculer la masse M_T de la Terre.

Données: G = 6,67.10-¹¹ S.I.

2) Mars a deux satellites naturels, Phobos et Deimos. Phobos gravite à 9380 km du centre de Mars avec une période de 7 h 39 min. Deimos a une trajectoire quasi circulaire de rayon r_D = 23 460 km et une période de révolution T D = 30 h 18 min .

a) Calculer la masse de la planète Mars à partir des caractéristiques du mouvement de Phobos, puis de Deimos.

b) Comparer les valeurs obtenues.

3) Au cours de la mission APOLLO XVII en 1972, le module de commande en orbite circulaire autour de la Lune, à une distance de 2 040 km du centre de celle-ci, avait une période de 8 240 s dans le repère sélénocentrique. Calculer la masse de la Lune.

UTILISATION DES ACQUIS

1 3 Station orbitale

La station orbitale SALIOUT, de masse 20 t, est en orbite autour de la Terre (rayon R_T). Son altitude varie entre 219 km et 278 km.

Données: go = 9,8 m.s^-2 et R_T = 6 380 km.

1) Quelle est la trajectoire de cette station dans le référentiel géocentrique? "

2) Quelle est l'altitude moyenne de SALIOUT?

3) a) Calculer sa période de révolution en admettant que la station orbitale décrit une trajectoire circulaire à cette altitude moyenne.

3) La comparer avec la période réelle qui est de 89,2 min.

16 Satellite de télévision directe

Le 2 avril 1989, ARIANE V30 a été lancée depuis la base de Kourou (proche de l'équateur, en Guyane) pour placer en orbite le satellite de télévision directe TÉLÉ X.

À l'issue du processus d'installation, le satellite est en orbite circulaire, dans un plan équatorial, à l'altitude h.

Données: masse de la Terre: M_T = 5,975.1024 kg, rayon équatorial: R_T = 6 380 km , constante de gravitation G = 6,670.10^-11 S.I., masse du satellite en orbite: m = 277 kg , altitude: h = 35 782 km et jour sidéral: To= 86164 s.

1 4 Télescope spatial HUBBLE

Le télescope spatial HUBBLE a été mis sur une orbite circulaire autour du centre T de la Terre. Il évolue à une altitude h = 600 km .

Ce télescope, considéré comme un objet ponctuel, est noté H et a une masse m = 12.10³ kg. Les images qu'il fournit sont converties en signaux électriques et acheminées vers la Terre par l'intermédiaire de satellites en orbite circulaire à une altitude égale à h_G = 35 800 km.

1) a) Appliquer la loi de l'attraction universelle de Newton au télescope situé à l'altitude h.

b) Donner, en fonction de m , go, R et h , l'expression littérale de la valeur de la force de gravitation qu'il subit.

c) Calculer la valeur de cette force pour h = h_H= 600 km.

2) Le mouvement du télescope est étudié dans le repère géocentrique dont l'origine est T.

a) Montrer que son mouvement circulaire est uniforme.

b) Exprimer littéralement sa vitesse v sur son orbite en fonction de R , go et h , puis la calculer en m.s^-1et en km.h^-1quand h = h_H = 600 km.

c) Déterminer sa période de révolution T_H
Données: R=6380km et go=9,80m.s-².

15~ Vol de COLUMBIA

On désigne par R le rayon de la Terre, supposée sphérique et homogène, M la masse de la Terre, G la constante de gravitation universelle et h l'altitude.

1) La navette spatiale COLUMBIA a été placée sur une orbite circulaire, à l'altitude h = 250 km .

Établir, dans un repère géocentrique. les expressions de la vitesse v de cette navette et de sa période de révolution T en fonction de go, R et h.

Données: R = 6 380 km et go = 9,80 m.s^-1.

2) Le plan de l'orbite de COLUMBIA passait le 28 novembre 1983 par Cherbourg et Nice. Ces deux villes sont distantes de 940 km. On néglige la rotation propre de la Terre.

Calculer l'intervalle de temps séparant les passages de COLUMBIA au-dessus de ces deux villes.

1) C1 Montrer que ce satellite, se déplaçant d'Ouest en Est, est géostationnaire.

2) C1 Pourquoi la base de Kourou est-elle « intéressante» pour la mise en poste de tels satellites?

17 Satellite sur orbite équatoriale

La fusée ARIANE V au moment du décollage a une masse de 7,50 t. La poussée de ses moteurs est 900. 10⁴ N.

1) A2 Calculer l'accélération de la fusée lorsqu'elle le sol, sachant que les moteurs exercent une force

2) C2 Avant d'être lancé en orbite géostationnaire, le satellite est placé sur une orbite équatoriale circulaire basse à 200 km d'altitude. Il tourne d'Ouest en Est, c’est-à-dire dans le sens de rotation propre de la Terre.
Déterminer, pour un observateur terrestre, L'intervalle de temps qui sépare deux passages successifs du satellite à la verticale d'un point de l'équateur.

3) A2 Ce satellite est placé sur orbite géostationnaire
Calculer sa vitesse angulaire dans le repère géocentrique.

Données: g_O = 9,8 m. s^-2 et rayon terrestre: R_T = 6 380 km.

1 8 Masse d'Uranus

1) B3 On donne la période de révolution et le rayon r de l'orbite des cinq satellites d'Uranus découverts depuis la Terre. Dix autres ont été découverts par la sonde interplanétaire VOYAGEUR 2 en 1986.

	T (jour)	r (km
Miranda	1,4135	130 000
Ariel	2,520	192 000
Umbiel	4,144	267 000
Titania	8,706	438 000
Obéron	13,46	586 000 000x:

a) Pour chaque satellite, calculer T² et r³.

b) Sur un système d'axes orthogonaux, porter en abscisses r³ et en ordonnées T², et ce, pour chaque satellite

2) B3 Montrer que cte (troisième loi de Kepler

3) C1 Calculer la masse d'Uranus en utilisant la droite tracée.

9 Masse de la Terre

1) A2 On suppose que la Terre a une distribution de masse à symétrie sphérique de centre O.

a) Donner l'expression de l'intensité du champ gravitationnel g créé par la Terre à une altitude h en de G, R_T, h et M_T (masse de la Terre).

b) En déduire l'expression littérale de M_T de go, G et R_T.

Calculer numériquement MT. (Historiquement, c'est ainsi, à partir de G, que M_T a été déterminée.)

Données: constante gravitationnelle: G = 6,67.10^-11 S.I., rayon de la Terre: R_T = 6 400 km et intensité du champ gravitationnel au niveau du sol: go = 9,8 m.s^-2.

Le tableau ci-dessous rassemble les valeurs numériques des périodes de révolution T et des altitudes h des orbites de quelques satellites artificiels de la Terre.

a) Montrer que les valeurs données dans le tableau permettent de vérifier la troisième loi de Kepler.

En déduire une valeur numérique de la masse MT de la Terre.

20 ARIANE

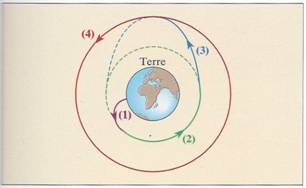
1-Lancement du satellite. 2. Orbite basse. 3. Orbite elliptique intermédiaire. 4. Orbite définitive.

Les différentes parties du schéma ne sont pas représentantes à la même échelle.

Voici un texte extrait d'un ouvrage scientifique: « Le lanceur européen ARIANE a été conçu pour placer en orbite géosynchrone, c'est-à-dire en orbite circulaire équatoriale située à 35 800 km d'altitude, des satellites qui restent immobiles dans le ciel et qu'on appelle satellites géostationnaires. Comme il serait trop onéreux de trop onéreux de propulser la fusée porteuse jusqu'à cette altitude, on procède par« transfert d'orbite».

base de	Kourou	Baïkonour	Chine	États-Unis
lancement	Kourou	Baïkonour	Chine	États-Unis
satellite	INTELSAT-V	COSMOS-1970	FEN-YUNI	U.S.A.-35
T	23 h 56 min	11 h 14 min	102,8 min	12h
h(km)	3,58.10⁴	1,91.10⁴	9,00.10²	2,02.10⁴

4) C1 Quelle signification l'auteur donne-t-il au mot « impulsion» ?

21 Etude d'un document

Ce document est une photographie du ciel nocturne. On observe sept satellites géostationnaires, notés A , B, C, D, E, F et G.

De gauche à droite: le GALAXY-III de la Hughes Aircraft Company sur la position 266,r (A) ; le S.B.S.-3 sur la position 265,2° (B) ; le TELSTAR de l'American Telephone and Telegraph Company sur la position 264,2°
(C) ; le S.B.S.-2 sur la position 263,2° (D) ; le WESTAR-IV de la Western Union and Hughes sur la position 261,2°
(E), de même que le S.B.S.-l (F) ; le dernier à droite est le S.B.S.-4 sur la position 259,2° (G).

1) a) C1 Cette photo n'est pas un instantané. Justifier cette affirmation.

b)C2 Calculer la durée de pause.

c)C2 Pourquoi les traces données par les étoiles sont-elles assimilables à des segments de droite?

2) a) C2 Pourquoi les images de ces satellites sont-elles alignées ?

b) Quelle distance sépare les satellites A et B ?

- Dans un premier temps, le satellite est placé par la fusée porteuse sur une orbite basse (200 km) ;

- dans un deuxième temps, le lanceur largue le satellite en lui fournissant une impulsion qui le place sur une orbite elliptique dont le périgée est à l'altitude 200 km et l'apogée à l'altitude 35 800 km ;

• dans un troisième temps, le satellite assure lui-même, par une deuxième impulsion, sa circulation en orbite circulaire.

Les deux premières phases du lancement s'effectuent grâce à trois moteurs entrant successivement en fonctionnement et qui sont largués après avoir rempli leur rôle. »

1) B1A1 Préciser l'expression utilisée par l'auteur: « satellites qui restent immobiles dans le ciel ».

À quel usage de tels satellites sont-ils destinés?

2) A2 L'orbite d'un satellite géostationnaire est-elle nécessairement une « orbite circulaire équatoriale»? Justifier la réponse, éventuellement à l'aide d'un schéma.

3) A2 Dans le repère géocentrique, quel est le sens de rotation du satellite: vers l'Est ou vers l'Ouest?