SUJETS MECANIQUE BAC MADA AVEC
CORRECTION
I -Bac D 2006
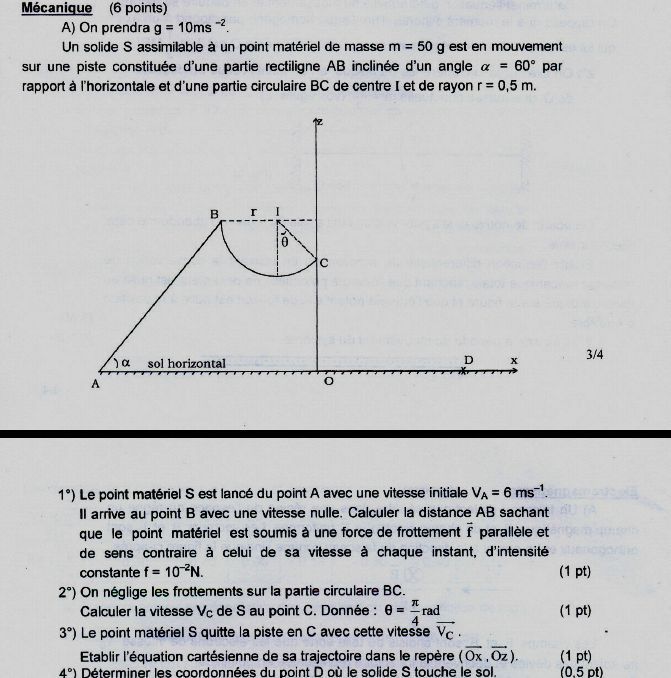
CORRECTION :
(Dans le
texte, les vecteurs sont représentés par des lettres en caractère gras .
Ex :le
poids P…)
1-Calcul de la distance AB :
L’étude du
mouvement du point est réalisée par rapport au référentiel terrestre galiléen.
Inventaire des
forces extérieures : le poids P
vertical, la force de frottement f
parallèle à la pente et de sens contraire au déplacement, la réaction R normale à la pente.
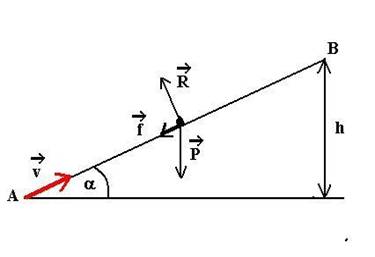
Appliquons le théorème de l’énergie cinétique :
Rappel de
l’énoncé du théorème: dans un
référentiel galiléen la variation de l’énergie cinétique d’un
solide est égale à la somme des travaux
des forces appliquées au solide pendant la durée de la variation.
Soit entre A et
B : Ec(B)-Ec(A)= W(f) +W(P)+W®
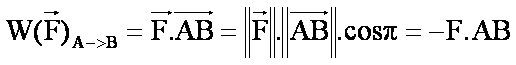
W®=0 car R est perpendiculaire à AB,
Soit h la dénivellation entre A et B ;
le travail de P ne dépend que de h
et comme il est résistant,
W(P) =-mgh=-mgABsina.
(Remarque f
désigne ici l’intensité (positive ) de la force)
Soit : 0 -
0.5m(vA)2=AB(-mgsina-f)
D’où :
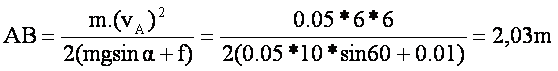
2-vitesse en C :
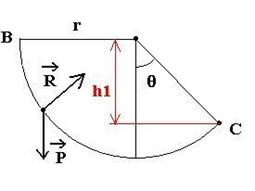
Inventaire des
forces extérieures : le poids P
vertical, la réaction R normale à la pente (les frottements
étant négligés).
Il est commode
ici encore d’appliquer le théorème entre
B et C:
Ec(C)-Ec(B)= W(R) +W(P).
Soit h1
la dénivellation entre B et C.
Le travail de P
est moteur, soit W(P) =+mgh1=
m.g.r.cosq.
Et W(R)=0 car R est perpendiculaire au déplacement à chaque instant.
L’équation
précédente s’écrit :
0,5.m.(vc)2=
m.g.r.cosq,
soit,
![]() .
.
3-Equation de la trajectoire :
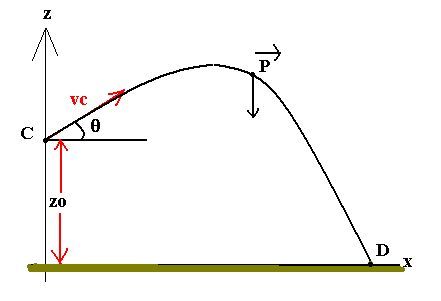
Le point est
soumis à la seule force P, c’est une
chute libre.
La relation
fondamentale de la dynamique (2éme loi de Newton) s’écrit :
![]() (1)
(1)
L’accélération du
point est donc constante, la trajectoire est parabolique.
Choisissons comme
instant initial t=0, celui du départ du point C(0,zo) .
zo=AB.sina -r.cosq = 2.02*sin60 -0.5*cos45=0.318m.
Projetons sur les
deux axes la relation 1 pour obtenir les équations paramétriques:![]()
![]()
Recherchons les primitives de ces
fonctions, soit en tenant compte des conditions initiales du mouvement :
![]()
Les primitives donnent :
x = (vc.cosq).t……et……..z =
-0.5.gt2+(vcsinq).t + zo![]()
En éliminant t
entre les deux équations : t=x/vc.cosq, on obtient l'équation de la trajectoire.
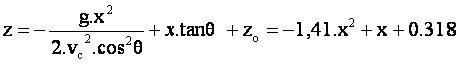
4. Abscisse du point de contact D :
Posons
z=0 ; soit : -1.41 x2+x+0.318=0.
xD est
la racine positive de l’équation soit :xD=+0.95m
II- Bac C 2008 (
Dans tout le problème, on néglige les
frottements et on prend pour l’intensité de pesanteur g =
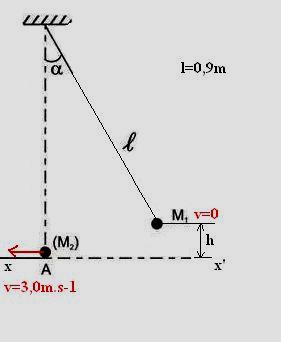
Un pendule simple est constitué
par une bille ponctuelle M1 de masse m1=
1) On écarte le pendule d’un angle a par
rapport à sa position d’équilibre verticale et on le lâche sans vitesse
initiale. La vitesse de la bille M1 lors de son passage à la
position d’équilibre est v =
2) Lors de son passage à la position
d’équilibre la bille M1 heurte, au cours d’un choc parfaitement
élastique, une autre bille ponctuelle M2 immobile de masse m2
=
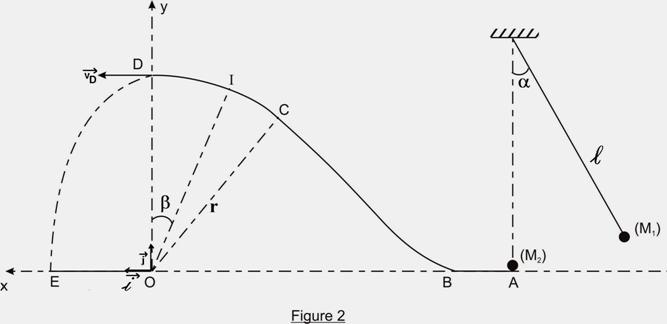
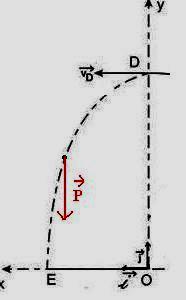
3) La bille M2 est propulsée avec la vitesse VA
sur une piste qui comporte trois parties : (figure 2)
-
Une partie horizontale AB,
- Une
certaine courbe BC,
- Un
arc de cercle CD, de rayon r et de centre O.
Les points O, A, B et E se trouvent dans un même plan horizontal.
a) Exprimer, en fonction de g, r, b et vA, la vitesse de la bille M2
au point I. (
b) Exprimer, en fonction de m2, g,
r, b et vA, l’intensité
de la réaction de la piste sur la bille M2 au point I. (
c) La bille M2 arrive au point D
avec une vitesse horizontale de valeur vD =
4) Arrivée au point D, la bille M2 quitte la piste avec
la vitesse ![]() précédente et tombe en
chute libre. (Figure 2).
précédente et tombe en
chute libre. (Figure 2).
a) Etablir l’équation cartésienne de la
trajectoire de la bille M2 dans le repère![]() . (1,5pt)
. (1,5pt)
b) Calculer la distance OE. (0,5pt)
= = = = = = = = = = = = = = = =
= = = = = =
CORRECTION
1-calcul de
l’angle a :
Dans le texte ci-dessous, la longueur du fil sera notée :L
Je propose ici une
solution énergétique.
Considérons deux
états du système déformable {bille, Terre}
Etat 1 : bille en M1,
vitesse v=0, hauteur y=h, énergie potentielle de pesanteur du système:
Ep(1)=mgh (si l’on prend le niveau x’x comme référence), énergie cinétique
Ec(1)=0
Etat 2 : bille en M2, vitesse v=3m/s, hauteur y=0, Ep(2)=0,
Ec(2)=1/2.m1.v2.
Les frottements
étant négligés, appliquons le théorème de conservation de l’énergie mécanique :
Ep(1) + Ec(1)=Ep(2) + Ec(2)
En remarquant que : h= L-L.cosa= L(1-cosa), il vient :
m1gL(1-cosa)=1/2.m1.v2.
et en simplifiant par m1 :
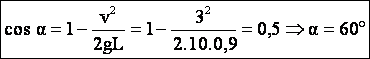
2-vitesse de la bille m1 juste
après le choc :
Le système des
deux boules étant isolé au moment du choc, il ya conservation de sa quantité de mouvement
totale :
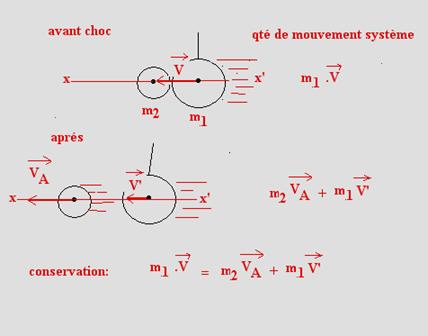
Projetons cette
relation sur l’axe x’x : m1 V= m2.VA+m1.V’,
soit :
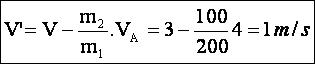 .
.
3-a Vitesse en I :
L’énergie
mécanique du système {bille/Terre} est
conservée lors du mouvement, et donc :
EC(A) + EP(A)= EC(I) + EP(I)
(1)
L’état de référence choisi du système est celui où la bille se trouve au niveau de l’axe x’x et donc EP(A)=0, la relation(1) s’écrit alors :
½.m2VA2=
½.m2VI2+m2.g.h(I) avec h(I)= r.cosb.
Et en simplifiant
par m2 : VA2=VI2 +2.g.r.cosb, soit
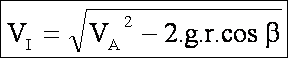 (2)
(2)
-b
Intensité de la réaction en I :
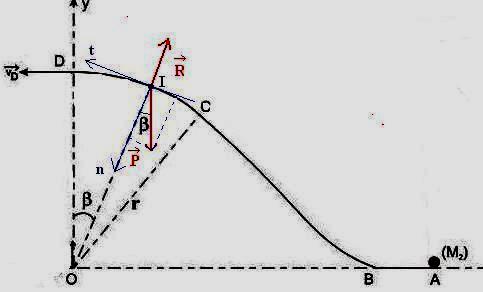
Les forces
appliquées sur la bille sont : le
poids et la réaction de la piste
(normale à la trajectoire en l’absence de frottement). Elles sont représentées
sur le schéma ci-dessous.
Le théorème du
mouvement du centre d’inertie appliqué à la bille s’écrit :
![]()
Projetons cette
relation sur l’axe In normal à la trajectoire et orienté vers
O.
Comme la
trajectoire est circulaire, la composante normale de l’accélération est :
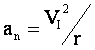
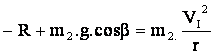
En tenant compte de la relation (2) précédente,
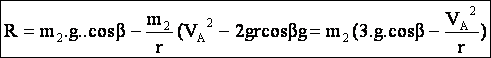
c-calcul de r :
Le
théorème de conservation de l’énergie entre A et D permet d’écrire:
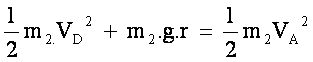
D’où l’on tire
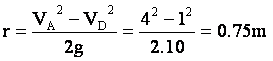
4-a Equation cartésienne de la trajectoire :
La bille est
soumise uniquement à son poids, elle est en chute libre.
Dans le
référentiel terrestre supposé galiléen, on a :
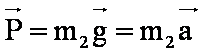
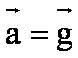
L’accélération
verticale est donc constante.
Précisons les
conditions initiales : à t=0, Vxo=VD=1,0m/s ,Vyo=0
(car la vitesse est horizontale) , y=yo=0,75m et x=xo=0..
Compte tenu de
celles-ci, les équations paramétriques du mouvement s’écrivent :
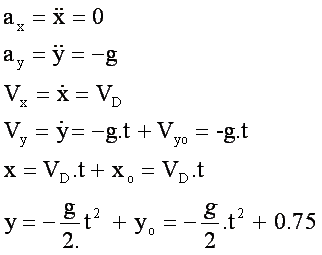
Eliminons t entre
x et y , il vient :
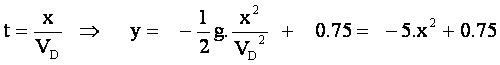
Equation d’une parabole d’axe de symétrie
Oy
4-b Calcul de OE :
Posons y=0, il
vient 5x2=0.75 soit x=+0.39m.
(La valeur
négative :-0.39 correspond à
l’abscisse du point symétrique qui ici n’a pas de signification physique).