EXERCICE I : MOUVEMENT CIRCULAIRE

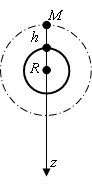
Un satellite de masse M décrit autour de la Terre d'un mouvement uniforme, une orbite circulaire à une altitude h.

Le rayon de la Terre est R = 6,4.10⁶m

L'accélération de la pesanteur est, pour h = 0, g_o = 9,81 m.s^-2 et, à l'altitude h,

1° - On suppose h = 300 km.

a) Calculer la vitesse du satellite sur son orbite.

b) Calculer la période de révolution.

2° - a) Quelle devrait être l'altitude h du satellite pour qu'il soit géostationnaire, c'est-à-dire qu'il apparaisse immobile à un observateur terrestre.

b) Calculer alors sa vitesse.

SOLUTION

1° - a) Vitesse du satellite sur une orbite d'altitude h = 300 km

Le satellite est seulement soumis à son poids et il est animé d'un mouvement circulaire uniforme sur une orbite de rayon r = R + h

Appliquons le principe fondamental de la dynamique est une accélération centripète de module

Projetons l'égalité sur un axe vertical, d'origine le satellite et orienté vers le bas. On obtient :

où g est l'accélération de la pesanteur à l'altitude h.

Comme , on a

Application numérique, comme :

on a :

1° - b) Période T de la révolution

Le mouvement étant uniforme, la période est le temps T, mis par le satellite, pour parcourir la longueur 2𝜋 (R + h) de la trajectoire d'où :

Application numérique, comme :

R+ h = 6,7.10⁶m et v = 7740m.s^-1, on a

ou T = 1h 30mn 30s

2°. a) Altitude h à laquelle évolue le satellite géostationnaire

Le satellite semble immobile pour un observateur terrestre lorsque :

· sa période de révolution est T = 24 h

· et le satellite a un mouvement de rotation autour de la Terre de même sens que le mouvement de rotation de la Terre.

On a trouvé au 1° :

d’où

Application numérique, comme :

T = 86400s, R = 6,4.10⁶m, g₀ = 9,81m.s ^{– 2}, on obtient

h = 42,36.10⁶ – 6,4.10⁶ = 35,960.10⁶m

Soit h = 35960km

b) Vitesse du satellite géostationnaire

on a trouvé

Application numérique, comme :

R + h = 42,36.10⁶m et T = 86 400s, on a

EXERCICE II

Soit un ressort d'axe vertical, de masse négligeable à spires non jointives, de coefficient de raideur k.

Une masse ponctuelle m est accrochée à l'extrémité inférieure du ressort (fig. 1)

1° - On écarte verticalement la masse m de sa position d'équilibre et on l'abandonne sans vitesse initiale.

Donner, sans démonstration, l'expression de la période T des oscillations de la masse m.

Application numérique :m = 0,36 kg, k = 49 N. m^-1

Calculer la période T.

b) Etablir la relation entre l'accélération et l'abscisse x de la masse m. En déduire la nature du mouvement et l'expression de la période T’.

c) Application numérique :calculer la période T’ des oscillations pour

k₁ = k₂ = 49N.m^-1 et m = 0,36kg

SOLUTION

1° - Période des oscillations de la masse m

La masse m est abandonnée sans vitesse initiale, et est soumise à son poids et à la tension du ressort dont le coefficient de raideur est k. Cette masse suit un mouvement rectiligne sinusoïdal de période

Application numérique : Comme m = 0,36 kg, k = 49N. m^-1, la période T est

2° - Allongements a₁, a₂

Etudions les forces s’exerçant sur les ressorts R₁ et R₂ isolément

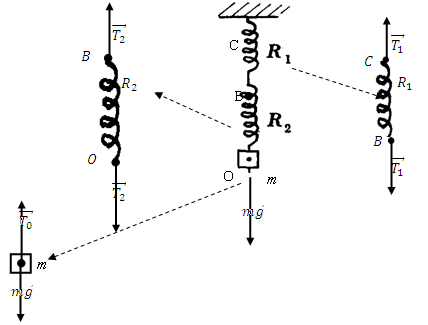
Forces s’exerçant Ensemble des Forces s’exerçant

sur R₂ deux ressorts sur R₁

Rappelons que, le système étant en équilibre, la tension d'un ressort de masse négligeable en un point est la force qu'il faudrait appliquer à chaque extrémité pour que le système reste en équilibre.

Ainsi le ressort R₂ est soumis en O à la tension = et en B à la tension .

Comme R₂ est en équilibre, la tension B est = - =

Le ressort R₁ est soumis en B à la tension et en C à la tension .

D’après le principe de l’action et de la réaction = - =

Comme le ressort R₁ est en équilibre : = - = -

Observons que la masse m est soumise, de la part du système des ressorts, en O à une tension opposée à (équilibre). Ainsi = =

= =

En somme, en tout point O, B, C du système, les tensions sont les mêmes. Exprimons la proportionnalité des modules des forces et respectivement aux allongements a₁ et a₂ (coefficients respectifs k₁, k₂) d’où : T₁ = k₁a₁ et T₂ = k₂a₂, ou comme T₁ = T₂ = mg

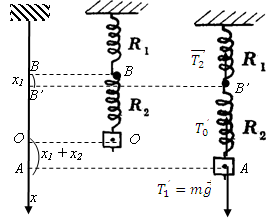
3° - a) Expression de x₁ et x₂ en, fonction de x, k₁, k₂

Le raisonnement relatif à la conservation de la tension dans le 2°) est encore valable parce que la masse m’ des ressorts est supposée négligeable. En effet soit par exemple G₂ le centre de gravité du ressort R₂ et γ₂ son accélération. La relation fondamentale de la dynamique s'écrit :