C3-Grandeur et position de l’image

 

1-Objectifs :

Etablir les différentes méthodes qui permettent de déterminer  la position et la grandeur de l’image donnée par une lentille mince convergente ou divergente utilisée dans les conditions de Gauss.

Résoudre quelques applications numériques. 

 

2-Relations  de conjugaison et de grandissement :

.

1,1- établissement des relations par le calcul :

Les relations à établir étant  algébriques, il faut choisir des conventions d’orientation.  

L’axe optique est  orienté positivement dans le sens de propagation de la lumière (ici de la gauche vers la droite).

On choisira  le centre optique O comme origine pour déterminer la position .

Les dimensions de l’objet et de l’image seront repérées sur un axe vertical orienté positivement vers le haut. La valeur d’une  flèche orientée vers le bas est négative.

 

 

 

Formule du grandissement :

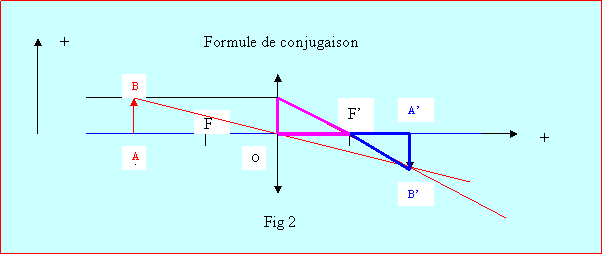
Les triangles OAB et OA’B’ sont homothétiques :

(1)                       

 

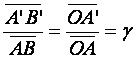
Formule de conjugaison :

 

Les triangles A’B’F’ (en bleu)  et OF’B (en violet) sont également homothétiques :

 

(2)

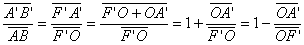
Les 2 expressions (1) et (2) étant identiques :

 

 

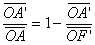
En divisant chaque terme de la relation précédente par 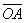, il vient :

 

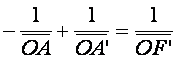
En notant : p=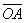 et p’= 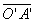et f’=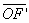,la relation devient :      

 

 

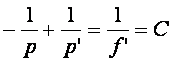
 1,2-établissement des relations par une méthode expérimentale  (à réaliser lors d’une séance de TP):

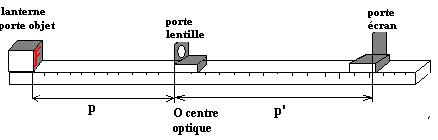
a- montage :

Placer une lentille convergente de vergence +5d  devant une lettre lumineuse. Choisir  la distance p  et former à chaque fois  l’image de cet objet sur un écran. Mesurer la distance p’ et la hauteur h’ de l’image.

L’idéal est de réaliser ce montage sur un « banc d’optique » : rail sur lequel les différents accessoires peuvent coulisser tout en restant parfaitement alignés ; les conditions de Gauss sont alors pratiquement toujours réalisées et le banc gradué permet de réaliser des mesures facilement.

 

 

L’expérience peut aussi être réalisée avec du matériel très simple : bougie, polystyrène, règle de classe, lentille récupérée chez un opticien local….

(Lycée Adoharanofotsy 2011)

 

 

Faute de matériel, il est possible aussi d’utiliser le logiciel de simulation sur banc d’optique, toutes les mesures ci-dessous ont été réalisées avec ce logiciel.

                                                  Simulations sur banc d'optique

 

b-mesures :

 

p (m)	p' (m)	1/p  (m-1)	1/p'  (m-1)	h' (cm)	h/h'	p/p'
-0,300	0,600	-3,333	1,667	-0,099	-0,505	-0,500
-0,400	0,400	-2,500	2,500	-0,051	-0,980	-1,000
-0,500	0,334	-2,000	2,994	-0,035	-1,445	-1,497
-0,600	0,300	-1,667	3,333	-0,025	-2,000	-2,000
-0,700	0,278	-1,429	3,597	-0,019	-2,632	-2,518
-0,800	0,268	-1,250	3,731	-0,018	-2,778	-2,985
-0,900	0,260	-1,111	3,846	0,014	3,521	-3,462
-0,260	0,873	-3,846	1,145	-0,168	-0,298	-0,298

 

c- exploitation:

La comparaison des deux dernières colonnes nous permet d’écrire  la relation de grandissement :

 

 

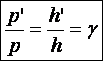
Traçer  le graphe de la grandeur  1 / p’ en fonction de 1 / p. A chaque point de celui-ci correspond les positions d’un couple (objet / image). 

Les points s’alignent ; la relation entre les deux est affine.

Dans excel, demander l’équation de la courbe de tendance. Ici, demander un modèle affine.

 

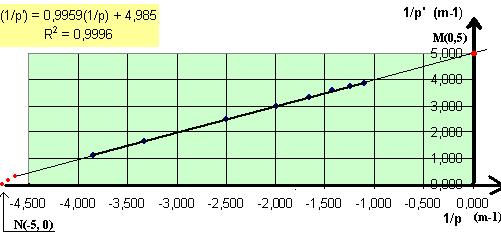
En prenant en compte toutes les mesures, on obtient la relation suivante :

 

 

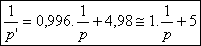
La pente de la droite est très proche de 1 et son ordonnée  à l’origine est voisine de 5.

L’intersection de la droite avec l’axe des ordonnées donne 5m^-1.C’est la vergence C=1/f’ de la lentille utilisée.

 

On retrouve bien la relation :

Les points d’intersection de la droite avec les axes correspondent à deux cas extrêmes de position de l’objet et de l’image.

-au point M :

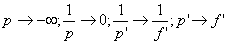
 L’objet AB est donc à l’infini à gauche et l’image se forme dans le plan focal image de la lentille.

-au point N :

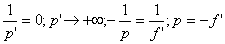
L’objet AB est dans le plan focal objet, l’image A’B’ est à l’infini à droite.

 

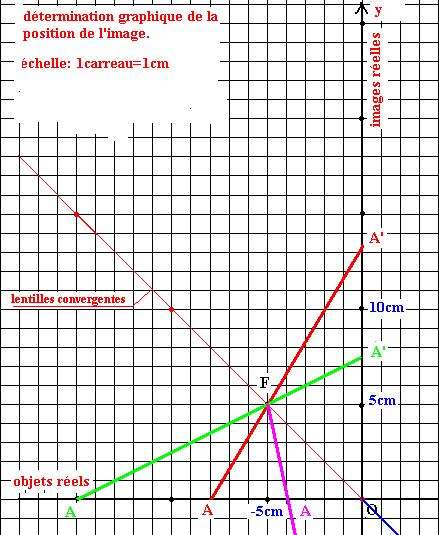
3-Détermination graphique de la position de l’image :

Dans un repère orthonormé, portons :

-en abscisse, la valeur algébrique :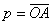

-en ordonnée, la valeur algébrique :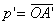

Sur le segment de droite qui joint le point objet A et le point image A’, repérons le point F unique situé à égale distance des deux axes Ox et Oy.  Ses coordonnées  sont :x_F=f et y_F=f ’et comme les coordonnées sont nécessairement de signes opposés, x_F=-y_F ,  f=-f ’.

 

/

 

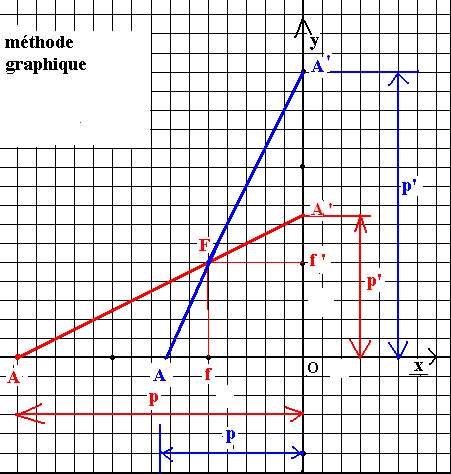La droite qui joint ces deux points a donc une pente égale à -p’/p et une ordonnée à l’origine égale à p’. L’équation s’écrit 

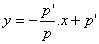
Les coordonnées de F (f,f ’) vérifient cette équation, et comme f=-f’ par hypothèse

.

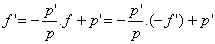Factorisons f ’, il vient :

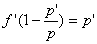
Divisons par f’p’ les deux membres  :

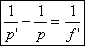
Les 3 grandeurs p, p’et f’ vérifient le formule de conjugaison des lentilles minces.

Les grandeurs f et f’ (avec f’=-f) sont donc les distances focales de la lentille utilisée.

Le point F caractérisant la lentille utilisée est donc un point invariant lorsque p et p’ varient. La droite précédente tourne donc autour de ce point suivant la position p et p’ de l’objet  et de l’image.

Cette méthode permet de déterminer rapidement la position de l’image connaissant celle de l’objet(ou vice versa) sans utiliser la formule de conjugaison et  sans faire la construction.

De plus, on peut connaître la nature de l’image (réelle ou virtuelle) suivant la position de A’ ainsi que  la dimension de l’image en comparant les distances OA et OA’.Le rapport permet de déterminer ensuite la taille de l’image h’.

 

4-Applications

 

4,1 Exemples 1 :

 

Compléter le tableau suivant .Indiquer dans chaque cas : le grandissement, la nature de l’image et citer un appareil utilisant la lentille dans cette condition. Les valeurs inscrites en bleues sont données.

 

Pos.objet p(cm)	Pos.image p’(cm)	Distance focale f’(cm)	Grandissement g	nature image	application
-15,0	7,5	5	-0,5	réelle	Appareil photo
-8,0	+13	5	-1,6	réelle	Projecteur diapos
-10	+10	5	-1	réelle	Mesure de f

Correction

 Ligne n°1 :

Méthode par le calcul :

f’=+5cm  et donc C=1/f’=1/0,05=20d.

    l’image est réduite et inversée. 

Construction de l’image : Simulations sur banc d'optique

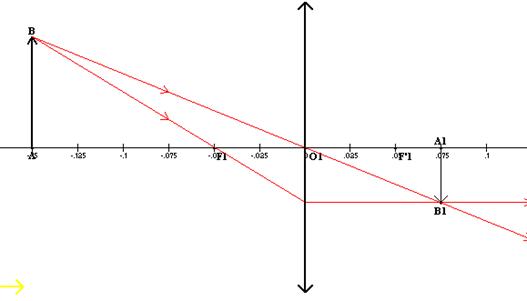
Méthode graphique :

-la ligne verte correspond aux valeurs de la  ligne n°1du tableau :

 

 

Ligne n° 2 du tableau :

Connaissant la position de l’objet et de l’image, il s’agit de déterminer la distance focale de la lentille.

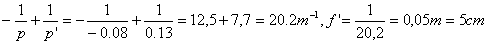
Ce cas correspond à la ligne rouge du graphe ci-dessus. L’image est réelle, agrandie, inversée. Application : optique d’un projecteur diapo.

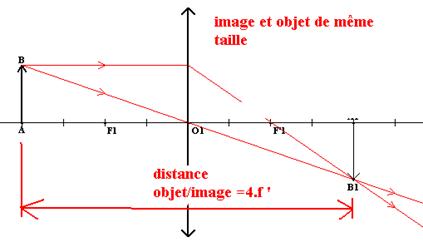
Ligne n°3 du tableau :

Dans ce cas p=-2f’ =-p’. et le grandissement est égal à -1.

Ce cas permet de déterminer la distance focale d’une lentille convergente.

On forme une image sur un écran de même taille que l’objet et inversée. Lorsque le réglage est réalisé, la distance objet /écran est égale à –p+p’=2f’+2f’=4f’

 

 

 

 

4,2 Exemple 2:

Soit une lentille de vergence 20 dioptries ( focale :5cm.)

Rechercher  la nature et la position de l’image d’un objet placé à  p= -4 cm devant la lentille (ce point se trouve donc entre le foyer objet et le centre optique), ainsi que la taille de l’image. Utiliser 3 méthodes différentes.

 

a-construction de l’image : Simulations sur banc d'optique

 

 

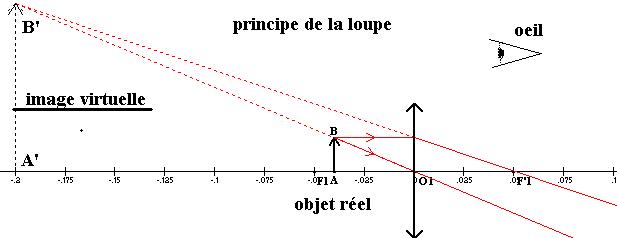
L’image n’est pas observable sur un écran , l’œil voit l’image en regardant vers la source à travers l’instrument d’optique. Pour l’observateur, les rayons lumineux semblent provenir de B’.L’image est virtuelle, elle est formée à 20 cm à gauche de O.

 

b-application de la formule de conjugaison :

 .

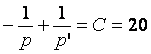
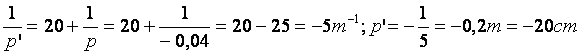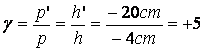   si h=1cm, h’=5cm

Retenons qu’un point image virtuel est placé au sommet d’un faisceau réfracté divergent. C’est le cas du point B’.

 

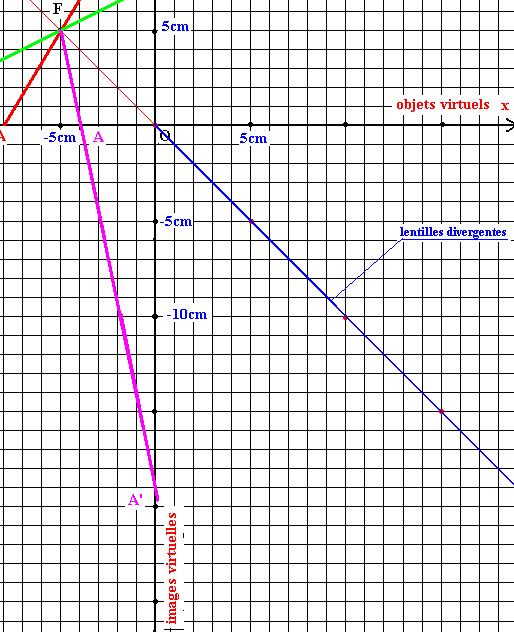
c-Méthode graphique (voir figure ci-dessus) :

Plaçons le point F(-5cm,+5cm) sur le graphe.

Traçons le segment AF (en mauve) que l’on prolonge jusqu’à l’intersection A’ avec l’axe Oy ; y_A’ est alors négatif, l’image est donc placée à gauche de la lentille et elle est virtuelle. Le grandissement est :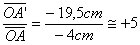                    

L’image est donc droite et 5 fois plus grande que l’objet.