« E=mc2 »
Source :http://www.astrosurf.com/astrotwins/Dossier/E=mc2.html:
Texte adapté par P
Baudoux pour les élèves de terminale de lycée
1-Objectifs :
Montrer les insuffisances de la mécanique de Newton.
Développer les fondements de la relativité restreinte
d’Einstein.
2. L'expérience de Bertozzi ou les
insuffisances de la mécanique de Newton :
a-description :
Voici
en quoi consiste l'expérience de Bertozzi qui a l’avantage d’être d’une grande
simplicité dans son principe. Elle date de 1964. On accélère des paquets
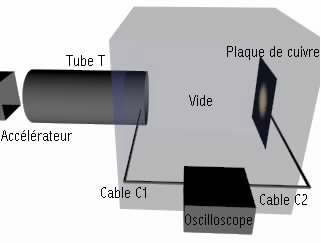
d'électrons ; à la sortie de l'accélérateur (voir figure ci-dessous), ils
passent dans une enceinte vide d’air. Ils parcourent une longueur de 8,4 m,
puis viennent frapper une plaque de cuivre..
En pénétrant dans l’enceinte certains électrons du
paquet sont captés par le cable conducteur C1, qui se charge négativement.
Lorsque les électrons frappent la plaque de cuivre, un 2ème signal
est recueilli par l'intermédiaire du câble C2 qui a la même longueur que le premier afin que les durées de propagation dans les fils soient le mêmes.
L’oscilloscope ayant une vitesse de balayage très grande détecte les deux
signaux décalés sur l’écran .L'écart entre les deux permet de mesurer le temps
de vol des paquets entre C1 et C2.
b-expression newtonienne de la vitesse des paquets à la sortie
du tube (rappel):
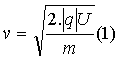 q= -1,6.10-19C est la charge de l’électron.
q= -1,6.10-19C est la charge de l’électron.
U : tension accélératrice entre
les deux extrémités du tube.
m = 9,1.10-31kg masse de l’électron
Les électrons conserveraient
ensuite cette vitesse entre C1
et C2. Remarquons que l’application de cette formule indique que si
U tend vers l’infini, V tend aussi vers l’infini !
c-Résultats des mesures :
L’expérience permet de mesurer la vitesse des paquets d’électrons en
divisant la distance de 8,4m par le temps de vol.
|
Energie cinétique
de l’électron
(MeV)
|
Temps de vol mesuré
(ns)
|
Vitesse observée
V
(x108m.s-1)
|
Vitesse(1) prévue
par la mécanique de Newton
(x108m.s-1)
|
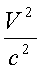
|
|
0,5
|
32,3
|
2,6
|
4,19
|
0,751
|
|
1,0
|
30,8
|
2,73
|
5,93
|
0,828
|
|
1,5
|
29,2
|
2,88
|
7,26
|
0,922
|
|
4,5
|
28,4
|
2,96
|
12 ,6
|
0,973
|
|
15,0
|
28,1
|
2,99
|
23
|
0,993
|
. Les résultats sont en désaccord avec l’expression
newtonienne
Quelle que soit leur énergie, la vitesse des électrons ne peut dépasser celle de la
lumière dans le vide. C=3.108m.s-1 apparaît comme
une limite infranchissable !
3-Expérience de Michelson-Morley
Expérience historique un peu plus délicate à comprendre et à réaliser
surtout ! Il a fallu plusieurs années (de1881 à 1887) pour la mettre au
point tend la précision requise pour la mener au bout est très grande.
a-A la recherche de
l’éther :
La nature ondulatoire de la lumière ayant été prouvée, les physiciens se
mirent à la recherche du milieu « absolu »immobile par rapport aux étoiles
dans lequel l’onde lumineuse se propagerait.. Ils le baptisèrent « éther ».
La lumière serait donc la propagation d’une perturbation de l’éther et
elle se déplacerait à la célérité c=3.108m/s par rapport à lui.
Par contre la Terre dans son mouvement de translation autour du Soleil évoluerait à 30km/s
par rapport à l’éther. Une expèrience d’optique devrait permettre de mesurer ce
« vent d’éther » sur notre planète. C’est l’objectif de l’expèrience.
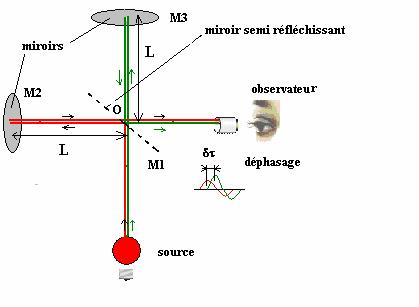
b- Le dispositif
expérimental (voir figure):
La lumière
provenant de la source monochromatique tombe sur un premier miroir M1
semi-réfléchissant et incliné à 45°.Le faisceau se partage en deux, une partie
se réfléchit et se dirige vers M2 et l’autre se dirige vers M3.En
se réfléchissant sur M2 et M3, les rayons parviennent dans l’oculaire où ils se
superposent après avoir suivi des chemins différents.
Les
longueurs L des « bras » du dispositif sont égales.
c- le calcul de la durée de chaque chemin
optique :
Appliquons
à la lumière la loi de composition des vitesses de la mécanique newtonienne.
Si la Terre se déplace à la vitesse u =30km/s par rapport a l’éther et dans
le même sens que le rayon lumineux, la vitesse totale de la lumière
serait :c+u, et si elle se
déplace dans le sens contraire, la vitesse est c-u, d’où le temps t1 mis par la lumière pour effectuer
le trajet aller et retour:OM2O
:
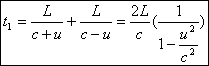
Pour
calculer le temps t2 mis pour effectuer le trajet OM3O, il
faut appliquer la loi de composition vectorielle des vitesses. Nous
admettrons le résultat :
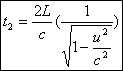
Ces durées
ne sont pas identiques et donc le décalage horaire t2-t1=dt n’est pas nul. Les deux faisceaux
présentent un déphasage en se superposant
L’application
de la loi de composition des vitesses de la mécanique prévoît donc un déphasage entre les deux faisceaux
arrivant dans l’oculaire del’observateur.
(Notons
qu’un déphasage supplémentaire existe du fait que les deux bras n’ont pas
rigoureusement la même longueur L mais ce dernier peut être compensé en
réalisant l’expérience une nouvelle fois après rotation de l’appareil de 90°).
Cette
expérience devait permettre de calculer la vitesse u de translation de la Terre par rapport à l’éther puisque le décalage dt dépend de u.
Aller à : Navigation,
Rechercher
d-Les observations de Michelson et Morley :
Le premier interféromètre monté par Michelson n'étant pas assez
précis, c'est avec Morley que finalement les deux chercheurs purent affirmer l’absence
de déphasage et donc la non validité des hypothèses sur la composition des
vitesses de la lumière avec la Terre.
Cette expérience est sans doute la plus célèbre des expériences
négatives (donnant un résultat contraire à ce qui était recherché).
Il faut abandonner le
concept d’éther et admettre que la célérité de la lumière est la même par
rapport à la Terre se déplaçant dans le
sens de la lumière ou dans le sens contraire !
e-Les postulats de la relativité :
1-La
vitesse c de la lumière est la même dans tous les référentiels galiléens,
quelle que soit la vitesse de la source.
2-Les
lois de la physique sont identiques dans tous les référentiels galiléens.
f-quelques explications :

Concrètement
cela signifie que la lumière émise par les phares d’un véhicule se déplaçant à
la vitesse de 90km/h est c=3.108m/s
par rapport au conducteur (ce qui n’est pas surprenant…) Le postulat de
la relativité nous dit que cette lumière se déplace encore à la vitesse c par
rapport au sol (et non c+90 !). Un véhicule roulant en sens inverse à 90,
recevra cette lumière encore à la vitesse c (et non c+180 !).
Une expérience
d’optique réalisée avec ce faisceau de lumière dans un labo lié au sol donnera
les mêmes résultats que le véhicule soit en mouvement ou pas.
Einstein
généralise le principe (mécanique) de relativité de Galilée :« aucune
expérience de mécanique ne permet
de mettre en évidence le mouvement rectiligne et uniforme du référentiel dans
lequel elle se déroule »
Einstein étend le principe de Galilée
à toute la physique. Ainsi le dispositif de Michelson est incapable de
montrer le mouvement éventuel du référentiel Terre.
Aucune expérience de physique ne peut mettre en évidence le mouvement rectiligne et uniforme du
référentiel galiléen dans lequel s’effectue l’expérience.
4- E=mc2: Comment cette formule permet le calcul de
l'énergie libérée par une réaction nucléaire.
Cette relation découle des 2
postulats cités plus haut, elle fut établie par Einstein en 1905 dans le cadre
de la théorie de la relativité restreinte. Elle permet par exemple
l’interprétation énergétique des réactions nucléaires ce que la mécanique
newtonienne ne peut pas faire. Notons que la mécanique relativiste ne
contredit pas la mécanique newtonienne tant que le domaine des
vitesses reste inférieur à une valeur de l’ordre de 30.000km/s (soit un
dixième de c). Le mouvement des planètes
ou des comètes est prévisible avec une très grande précision avec la mécanique newtonienne !
1. L'équivalence entre la masse et
l'énergie
Par des techniques très précises, il est possible de mesurer la masse d'un
noyau et celle d'un proton isolé ou d'un neutron isolé. Il s'avère que la masse
du noyau est inférieure à la somme des masses de chacun de ses nucléons.
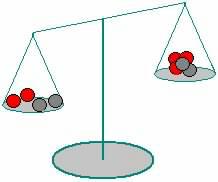
Alors où est passée cette masse? Et bien elle s'est transformée en énergie. Cette quantité d'énergie est
appelée énergie de liaison et elle correspond à l'énergie qu'il faut fournir au
noyau pour qu'il soit dissocié en nucléons .
Considérons
le diagramme d’énergie du système de nucléons.
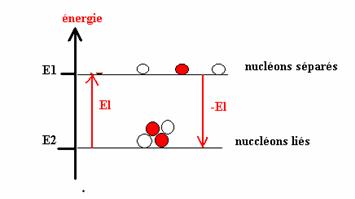
Le niveau
d’énergie E2 correspond à l’état lié où les noyaux interagissent
entre –eux pour former le noyau. C’est l’état le plus stable.
Le niveau E1
correspond à l’état de rupture du noyau en ses nucléons séparés. C’est un état
instable car les nucléons supposés proches les uns des autres sont sensibles à
l’interaction nucléaire qui tend à les souder.
Il faut
fournir une l’énergie égale à l’énergie de liaison El=E1-E2
pour rompre le noyau. Inversement, lorsque le noyau se forme à partir de ses
nucléons, le système libère une énergie égale à –El. Dans ce dernier cas le
système libère de l’énergie.
Au cours de
cette transformation 1à2 La
relation d’Einstein s’écrit :
E2-E1=(m2-m1)c2=
Dm.c2 avec Dm<0 car le système
libère de l’énergie .
La relation
d’Einstein stipule qu’il y a équivalence entre la masse et l’énergie.
Une perte de
masse équivaut à une libération d’énergie du système.
DE= DM.c2.
Il est
évident que l’énergie de liaison croît
avec le nombre de nucléons et donc avec la taille du noyau. Pour autant, il ne
faudrait pas conclure que les noyaux les plus gros sont les plus stables !
C’est plutôt le contraire ! Si un seul nucléon se libère, c’est tout
l’édifice qui s’écroule. C’est l’énergie de liaison par nucléon qui caractérise
sa stabilité.Pour un noyau comprenant A nucléons (nombre de masse), c’est le
rapport El/A (énergie de liaison par nucléons) .
2. La fusion nucléaire
Pourquoi une
réaction de fusion libère-t-elle de l'énergie?
La somme des masses de 2 petits noyaux est plus importante que la masse de
leurs noyaux fusionnés. Or d'après DE=Dmc2 , si m diminue lors de la formation du
noyau (perte de masse du système:Dm<0)
alors le système libère une énergie équivalente DE.
On peut calculer cette
énergie lors de la réaction suivante:
21H + 31H => 42He
+ 10n
Bilan énergétique de la
transformation :
On donne les masses des particules en unités de masse
atomique :
|
particule
|
masse en u(*)
|
|
Noyau de
deutérium :12H
|
2,01345
|
|
Noyau de
tritium : 13H
|
3,01550
|
|
Noyau d’hélium :
24He
|
4,00150
|
|
Neutron 11n
|
1,00866
|
Variation de masse de masse : Dm=4,00150+1,00866-3,01550-2,01345= -0,01879u.
Energie libérée par noyau d’hélium formé : DE=-0.01879u.c2.931(**)Mev/c2=-17,5Mev.
Soit en joules : DE=-17,5.106.1,6.10-19=28.10-13J.
Soit, pour une mole de noyaux formés : 28.10-13.6.02.1023=
168.107kJ/mol.
Comparons cette énergie à la combustion de 1 mole de méthane :891kJ.mol-1 .
Cela représente une
énergie environ 2 millions fois plus grande pour la fusion de l’hélium!
(*) unité de masse atomique = c’est la masse égale à 1/12 de la masse d’une
mole d’atomes 612C
-donc un atome(noyau + électrons) de carbone 12 aune masse très
exactement égale à 12,0000u
(**) l’énergie correspondante à 1 unité est 931 MeV/c2.
Ces unités sont beaucoup plus
pratiques avec des particules élémentaires.
