TP : DECROISSANCE RADIOACTIVE

1-Objectifs du TP :

-Définir la grandeur activité pour un échantillon radioactif

-Tracer la courbe de l’activité au cours du temps de l’échantillon et la modéliser.

-Montrer le caractère aléatoire de la désintégration d’un noyau et la prévisibilité du comportement d’un grand nombre de noyaux

-Mesurer la « demi-vie :T_1/2 »et la « constante radioactive : l » d’un élément radioactif.(¹³⁷Cs ou ⁶⁰Co).

2- Outil informatique nécessaire et définition:

Ce TP nécessite l’utilisation du logiciel « nucléaire » à charger dans l’ordinateur local, d’un tableur pour exploitation des mesures et d’un logiciel de simulation « jeu de dés » accessibles par des liens.

Pour télécharger le logiciel à partir de la médiathèque, cliquer sur le lien ci-dessous :

Radioactivité:simulation avec le logiciel "nucléaire"

Définition : l’activité d’un échantillon radioactif est le nombre de désintégrations par seconde . L’unité d’activité est le becquerel (Bq)

(1 becquerel correspond à 1 désintégration d’un noyau par seconde)

1Bq =1s^-1.

3-Mode opératoire :

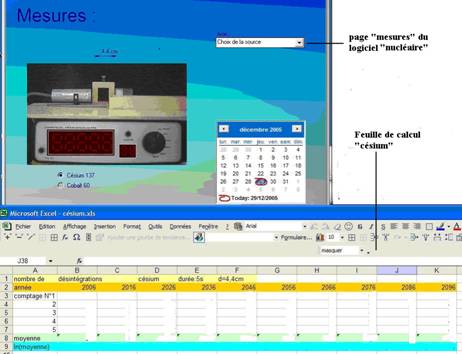
Ouvrir le logiciel « nucléaire » à la page « mesures ».

Nous voyons apparaître un ensemble de simulation de comptage analogue au dispositif « C.R.A.B » ( dispositif de comptage radioactif pour les lycées ) utilisé dans les lycées

Cet ensemble de simulation comprend, comme le C.R.A.B réel :

-une source radioactive mobile (au choix :césium 137 ou cobalt 60),

-un détecteur type Geiger relié à un dispositif de comptage du nombre de désintégrations.

La source radioactive se désintègre de façon aléatoire comme le ferait une véritable source ayant les mêmes caractéristiques.

L’appareil mesure le nombre de désintégrations traversant le détecteur pendant une durée choisie. Ce nombre est proportionnel à l’activité définie ci-dessus.

Régler les différents paramètres de comptage :

source : césium, distance source- détecteur : choisir 4,4cm, durée de comptage : choisir 5s, choisir la date initiale de comptage (par défaut c’est la date du TP qui est choisie).

3- Collecte des mesures :

Radioactivité:tableur d'exploitation pour TP

Placer le document « césium.xls » en réduction à proximité du compteur pour faciliter le report ou noter les mesures sur un brouillon et les reporter ensuite sur le tableur.

…ou créer un autre document à partir du logiciel Excel de votre ordinateur.

Faire 5 comptages pour chaque date choisie .Constater les valeurs différentes obtenues pour chaque comptage, prendre la valeur moyenne des cinq valeurs des activités mesurées.

Faire des comptages tous les 10 ans jusque l’an 2100 environ, saisir les mesures au fur et à mesure dans un tableau préparé dans le document Excel « cesium.xls ».(voir document ci-dessus )

4-Tracé des graphes et modélisation:

a/Demander le traçage des 2 graphes suivants :

-nombre de noyaux de l’échantillon radioactifs restants en fonction de la date :

-logarithme népérien de A en fonction de la date

Utiliser la fonction « courbe de tendance » pour modéliser les deux graphes.

On pourra faire une deuxième série de mesures avec une source de cobalt

Correction : tracé des graphes et modélisation

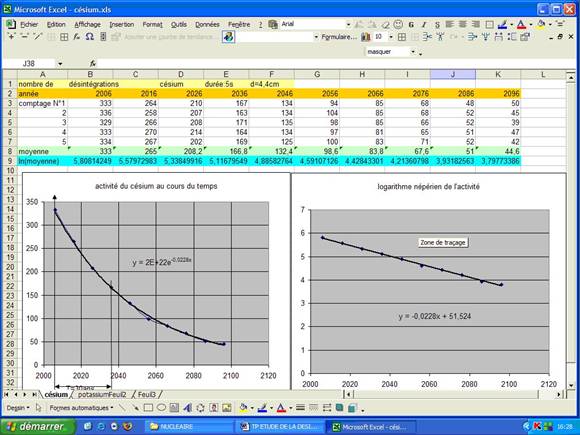
b-Définition :

la demi vie : T_1/2 est la durée nécessaire pour que l’activité moyenne d’un échantillon soit divisée par deux.

Pour le césium 137 on trouve T_1/2=30ans (voir graphique ci-dessus)

(éviter absolument le terme « période » qui est impropre).

c-Interprétation et modélisation de la courbe de décroissance:

Le deuxième graphe est une droite de pente négative ce qui prouve que l’activité est une fonction exponentielle décroissante du temps. Comment expliquer cette loi exponentielle ?

--Une analogie intéressante : le jeu de dés.

Règle du jeu: lançons un jeu de No=100 dés sur une table ! Eliminons tous les dés qui donnent un 6 .Rassemblons les N₁ dés restants et lançons ce nouveau paquet sur la table. De nouveau tous les dés qui donnent 6 sont éliminés .Soit N₂ le nombre de dés restant...On poursuit le jeu aussi loin que possible. Et l’on trace la courbe N restant en fonction du nombre de jet

Le nombre de dés restant: No,N₁,N₂..etc suit une loi de décroissance analogue au nombre de noyaux restants d'un échantillon au cours du temps.  

C’est que l’événement «  désintégration d'un noyau », comme « l'obtention d'un 6 » est aléatoire. On ne peut pas prédire avec certitude si un noyau va se désintégrer dans l'heure qui suit, comme on ne peut pas être certain que le dé va tomber sur le 6! On ne peut que donner une probabilité de désintégration ou une probabilité d'obtenir le 6.Il existe de plus une similitude sur les caractères de cette décroissance :aucun traitement physique ou chimique ni l'âge de l'échantillon radioactif ne modifiera cette probabilité de désintégration d'un noyau. De même, la probabilité d'obtenir un 6 avec un dé est toujours de 1/6 au 1er jet comme au dernier! La radioactivité comme le jeu de dés suivent la même loi statistique de décroissance

Un logiciel de simulation « jeu de dés » permet d'effectuer (virtuellement) le lancer d'un trés grand nombre de dés à la fois. Le comptage des 6 et des dés restants est bien entendu automatique ! Cliquer sur le lien ci-dessous pour y accéder

Radioactivité:simulation du caractère aléatoire de la désintégration

--Mise en forme mathématique de la loi de décroissance :

Considérons l’échantillon à la date t .S’il contient encore à cette date N noyaux radioactifs susceptibles de se désintégrer. Aucun noyau n’ayant plus de chance qu’un autre de se désintégrer, le nombre de noyaux qui se désintègreront pendant une durée Dt au-delà de t est simplement proportionnel à N, soit : DN=-l.N.Dt(1)

l est donc la probabilité de désintégration d’un noyau par unité de temps.

L’expression (1) indique que la dérivée de N est proportionnelle à N, ce qui est en accord avec une loi exponentielle comme le montrait l’étude expérimentale.

N=No exp(-l t).

lest une constante pour un isotope donné, c’est la « constante radioactive », elle vaut ici l=-0.0228 année^-1.

(pour le jeu de dés cette constante est 1/6 !)

Quand T _½ décroît, l augmente et vice versa.

On peut utiliser l’une ou l’autre grandeur pour caractériser la décroissance

On montre facilement que :

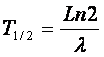
soit ici : T= 30ans

Conclusion : si le comportement d’un noyau est imprévisible, celui d’un très grand nombre de noyaux (échantillon radioactif) est très bien connu par la connaissance de ces constantes .On peut déterminer par exemple la date d’un ossement ancien à partir de la mesure de son activité par comparaison à l’activité d’un même ossement récent. La loi de décroissance étant connue, il est possible de dater la mort de l’échantillon ancien (voir exercice sur la datation).