EXO 1
Calculer, en M.e.v par nucléon, l’énergie
de liaison du noyau de lithium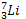
. On donne
Masse du neutron : 1,00566u
Masse du proton : 1,00866u
Masse du noyau de lithium :
7,016101u
1u = 931,5Mev/c2
EXO 2
On considère les 2 nucléons suivants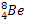 
; 
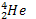
1. a/ Donner la composition du noyau de
chaque nucléide
b/ Le béryllium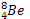 
se transforme en hélium suivant la réaction de
désintégration suivante :
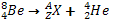. Identifier l’élément 
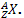Calculer l’énergie libère par cette réaction.
2. a/ Le béryllium se désintègre avec une
période T = 40mn. Un échantillon de béryllium 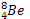à une activité initiale de 4,4.107Bq. Calculer
la constante de désintégration radioactive λ en S-1
b/ Quel est le nombre des noyaux de
Béryllium présents dans l’échantillon.
c/ Quelle est la masse de béryllium
correspondante à ces nombres des noyaux
3. a/ Combien restera t-il de noyau
radioactifs de 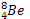dans cette échantillon après l’instant
t1 = 2h40mn ?
b/ Déterminer l’activité de Béryllium
dans l’échantillon à l’instant t1
c/ Déterminer l’instant t2
nécessaire pour que 99% de 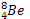se désintègre totalement.
d/ Calculer l’énergie de liaison par
nucléon du Béryllium
On donne : masse de Be = 8,0029u ;
mHe = 4,0015u
N = 6.1023 ;MBe =
8g/mol ; 1uma = 931,5Mev/c2
Log2 = 0,693 ; Log 10 = 2,3
EXO 3
L’osmium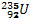 
est un isotope de l’osmium qui émet un rayonnement α
1. a/ Donner la composition du noyau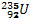
b/ Qu’appelle-t-on isotope, donner des
exemples
c/ Calculer en (Mev) l’énergie de liaison
par nucléon de l’uranium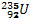
2. a/ Ecrire l’équation de désintégration
de l’uranium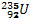
b/ Quel est le noyau obtenu
c) Un échantillon d’uranium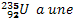 
masse 1g à l’instant t = 0s. La période radioactive est
T = 7.10+8 années. Calculer
l’activité de cet échantillon à l’instant t1 = 2,1.109ans.
On donne : nombre d’Avogadro N = 6.1023 1µ.ma = 931,5Mev/c2.
Masse de l’uranium 235 = 234,9944u.
1an = 3,16.107 02cm. Extrait
du tableau périodique 
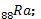
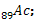
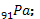
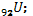
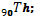
EXO 4
Le nucléotide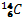 
est radioactif (radioactivité B-) Sa période ou
demi vie est 5.500 ans
1. Définir la période radioactif
2. Ecrire l’équation de sa désintégration
3. Soit un échantillon contenant ce seul
nucléide radioactif qui a une activité correspondant à 16 électrons émis par
seconde. Au bout de combien de temps cette activité sera – t – elle réduite à
4é émis par seconde ?
EXO 5
La période du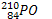 
est de 38ans
1. Calculer la conbrite radioactive de ce
nucléide
2. A
partir de 1g de polonium, quelle est la masse restante au bout de 1j, 1an,
10ans, 100ans, 1000ans ?
EXO 6
Le tritium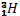 
se désintègre avec une constante radioactive λ =
1,786.10-9s-1
1. Quelle est la période radioactive.
Donner le résultat en année
2. On considère une masse de tritium qui
donne 2.106 désintégrations par seconde. Quelle est la valeur de
cette masse ?
On donne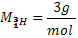 
; N = 6,022.1023
EXO 7
Le plutonium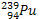 
est radioactif et émetteur α. Sa période (demie vie)
est T = 24.00ans.
1. Ecrire l’équation de la transformation
radioactive
2. Calculer la masse d’uranium 235 et
d’hélium formés au bout de 10ans à partir d’une masse de 10g de plutonium 239.
EXO 8
Le bismuth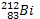 
est radioactif et émetteur α
1. Ecrire l’équation de désintégration.
Quel est l’élément formé ?
Extrait du tableau périodique des
éléments : 
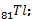
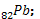
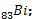
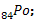
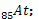
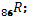
2. Soit une source radioactive contenant
initialement 8,1g de bismuth radioactif. Grâce à un compteur, on a montré qu’il
s’y produit, a partir de l’instant initial, 4,484.1019
désintégrations en 15 minutes. Calculer la période radioactive du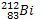 
; N = 6,02.1023 le nombre d’Avogadro
3. Calculer le volume d’hélium produit en
30 minutes (volume mesuré dans les conditions normales) par cette source
radioactive. MBi = 212g/mol
EXO 9
Délation du carbone 14
1. Dans la haute atmosphère, sous l’effet
du bombardement neutronique, l’azote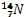 
se transforme en carbone 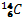radioactif. La désintégration de ce carbone 14 donne de
l’azote 14. Ecrire les équations de ces 2 réactions nucléaires.
2. La période du carbone 14 est 5590
années, il permet d’effectuer des datations un échantillon de charbon de bois,
trouve dans une grotte préhistorique, donne a partir d’un jeune bois, donne
1350 désintégrations par minute. Quel est l’âge de l’échantillon des bois
ancien ?
EXO 10
Radioactivité α et ﻻ
Le bismuth 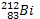est radioactif émetteur α
1. Ecrire l’équation de la réaction
nucléaire
2. Les vitesses sont suffisamment faibles
pour que la mécanique newtonienne soit applicable. En exprimant la conservation
de la quantité de mouvement, montrer que l’énergie cinétique dite « de
recul » du noyau forme ECr est égal à la fraction 4/208 de
l’énergie cinétique de la particule α qui se sera notée ECα.
Le noyau de bismuth est initialement au repos.
3. Dans cas précis, on a mesuré l’énergie
cinétique d’une particule α émise : ECα = 5762 keV,
on a également mesuré l’énergie fournie par expérimentaux permettent – ils de
conclure qu’il y a conservation de l’énergie lors de la désintégration ?
4. En fait, l’émission α
s’accompagne de l’émission d’un rayonnement ﻻ. Calculer la longueur
d’onde des radiations ﻻ émises dans le cas envisagé ici. On donne H =
6,62.10-34SI C = 3.108ms-1 1ev = 1,6.10-19J
EXO 11
Equilibre radioactif
Le radionucléide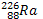 
subit une désintégration de type α.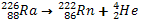 
1. On désigne par N0 le nombre de noyaux
de radium existant dans échantillon à la date t = 0 et par n le nombre. Les
noyaux subsistant à la date t. la période ou demi vie du radium est T = 1620
années. On considère 1g de radium fraîchement préparé. Calculer l’activité de
cet échantillon : -dn/dt = nombre de noyaux de Ra désintégré pendant 1s
dans cet échantillon, et montrer qu’il peut être considéré comme constant
pendant une durée faible devant T.
2. Le Radon Rn étant radioactif, les
noyaux de radon formés se désintègrent à leur tour avec une période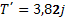 
. Après quelques semaines, la masse de radon se stabilise
(c'est-à-dire constante) un équilibre radioactif s’est réalisé entre les
masses de radium et de radon en présence.
a/ Comparer les activités des radium et
du radon en présence, lorsque l’équilibre est atteint.
b/ En déduire la masse et le volume (CN)
de radon en équilibre radioactif avec 1g de radium. (le radon est un gaz
parfait monoatomique)
EXO 12
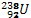est un élément radioactif naturel qui par désintégration
successives de types α et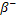 
donne 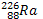lui-même radioactif. Ceci conduit enfin selon des processus
analogues, à un isotope non radioactif abble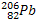 
1. La première désintégration de
l’uranium est de type α
a. Ecrire l’équation de cette réaction
nucléaire en défiant le radioélément formé parmi les suivants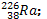 
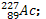
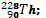
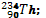
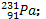
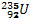
b. Déterminer les nombres a de désintégration
de type α et b de désintégration de type 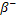néconaires jour évoluer de 
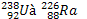. Même question jour le passage de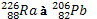 
2. La masse du noyau de 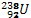est 238,08604U, celle du noyau formé après désintégration
234,07814 et celle d’une échelle α : 4,0026U.
a. Calculer le module de la vitesse
d’émission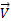 
des particules α en admettant que toute l’énergie
liberée au cours de la réaction nucléaire contribue à l’énergie cinétique.
b. Justifier que la valeur trouvée
autour l’emploi de la mécanique clonique 1µ = 466.10-27kg c =
300.000km/s
EXO 13
Désintégration α Energie
Le radium 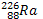est radioactif et émetteur α
1. Ecrire l’équation de la désintégration
2. En utilisant la mécanique classique et
en écrivant la conservation de la quantité de mouvement et de l’énergie,
montrer que la particule α emporte la quasi-totalité de l’énergie libérée
par la désintégration.
3. En admettant que chaque particule
α émise a une énergie cinétique de 4,7M.e.v, calculer en joules l’énergie
libérée par la désintégration complète de 1mg de radium. Quelle est la perte de
masse correspondante. Calculer également le rapport entre la perte de masse et
la masse de radium désintégré. C = 300.000km/s N
= 6,02.1023
EXO 14
Fission nucléaire
1. Ecrire l’équation de la réaction
nucléaire correspondant au bombardement d’atomes de bore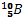 
par des neutrons pour former une particule α et un
noyau de lithium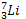
2. Quel est en Mev, le bilan énergétique
de cette réaction nucléaire ?
3. Calculer, en joules, l’énergie obtenue
par la réaction complète de 1 g de bore ?
On donne : masse des particules B =
10,01294u neutron = 1,00867u
α = 4,0026u ; Li =
7,01600u
N = 6,02.1023
