Comparaison entre l’énergie libérée par une réaction nucléaire de fission et par la combustion du pétrole.

Source :http://physique.chimie.pagesperso-orange.fr/  

ENONCE :

En 1999, la France a produit une énergie électrique de 486 ´ 10 ⁹ kWh. Plus de trois quart sont d’origine nucléaire. Le but de cet exercice est de montrer l’intérêt énergétique de ce choix.

DONNÉES

La production d’énergie dans ces réacteurs repose sur la fission de l’uranium 235.

Lorsqu’un neutron heurte un noyau d’uranium 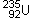, une des fissions possibles conduit à la formation d’un noyau de cérium 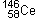, d’un noyau de sélénium 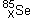, ainsi qu’à un nombre a de neutrons.

· 1- Écrire l’équation complète de cette réaction nucléaire ; en déduire la valeur de a et celle de X. Justifier en exprimant les lois appliquées.

· 2- Calculer la variation de masse Dm qui accompagne la fission d’un noyau d’uranium 235

· 3- Calculer, en joule et en MeV, l’énergie DE libérée par cette réaction.

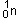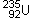On considère que les énergies cinétiques initiales du neutron et de l'uranium sont négligeables devant leur énergie de masse

· 4- Les centrales nucléaires françaises utilisant de l’uranium 235 fournissent au maximum une puissance électrique P = 1455 MW.

La combustion d’un kilogramme de pétrole libère une énergie E = 45 ´ 10 ⁶ J sous forme de chaleur. Le rendement de la transformation d’énergie thermique en énergie électrique est de 34,2 %. En déduire la masse de pétrole qui serait nécessaire pour produire pendant un an la même énergie électrique que les centrales nucléaires françaises.

SOLUTION :

· 1- Equation de la réaction de fission

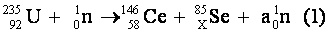
La loi de conservation de la charge électrique permet d'écrire :

92 + 0 = 58 + X + a ´ 0

X = 34 (2)

La loi de conservation du nombre de nucléons permet d'écrire :

235 + 1 = 146 + 85 + a (3)

On obtient X = 34 et a = 5.

 Portons dans l'équation (1) :

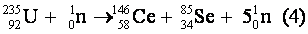
· 2- Calcul de la variation de masse Dm qui accompagne la fission d’un noyau d’uranium 235.

Calculons tout d'abord, en unité de masse atomique, la masse d'un neutron :

m ( 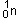) = 1,6749 ´ 10 ^{- 27} kg = 1,6749 ´ 10 ^{- 27} / 1,6606 ´ 10 ^{- 27} = 1,0086 u (5)

D'après (4), la variation de masse qui accompagne la fission d’un noyau d’uranium 235 est :

Dm = masse finale - masse initiale

D m = (145,8782 + 84,9033 + 5 ´ 1,0086) - (234,9935 + 1,0086)

La masse du système diminue (Dm est négatif). Cette disparition de masse provoque une apparition d'énergie.

· 3-Calcul de l'énergie DE libérée par cette réaction.

On considère que les énergies cinétiques initiales du neutron et de l'uranium sont négligeables devant leur énergie de masse.

L'énergie que la réaction dégage s'écrit, en valeur absolue :

½ DE ½ = ½ Dm ½ ´ c² (7)

Calculons Dm en kg (l'énoncé rappelle que 1 u = 1,6606 ´ 10 ^{- 27} kg) :

½ Dm ½ = 0,1826 u = 0,1826 ´ 1,6606 ´ 10 ^{- 27} = 3,032 ´ 10 ^{- 28} kg (8)

Portons dans la relation (7) :

½ DE ½ = ½ D m ½ ´ c² = 3,032´ 10 ^{- 28} ´ (2,9979 ´ 10 ⁸ ) ²

- Calculons cette énergie en MeV.

L'énoncé rappelle que e = 1,602 ´ 10 ^{- 19} C (10). On peut ainsi retrouver que :

1 MeV = 1 ´ 10 ⁶ ´ (1,602 ´ 10 ^{- 19} C)V = 1,602 ´ 10 ^{- 13} CV = 1,602 ´ 10 ^{- 13} J

Soit :

1 J = 6,24219 ´ 10 ¹² MeV

On peut donc écrire :

½ DE ½ = 2,724981 ´ 10 ^{- 11} J = 2,724981 ´ 10 ^{- 11} ´ 6,24219 ´ 10 ¹² = 170,09849 MeV

Finalement :

· 4- Masse de pétrole qui serait nécessaire pour produire pendant un an la même énergie électrique que les centrales nucléaires françaises

Calculons la durée en secondes :

t = 1 an = 365 jours = 365 ´ 24 heures = 365 ´ 24 ´ 3600 secondes

t = 31536000 s

Calculons l'énergie électrique fournie par les centrales nucléaires, en 1 an :

W = P ´ t = (1455 ´ 10 ⁶) ´ (3,1536 ´ 10⁷) = 4,589 ´ 10 ¹⁶ J (12)

- La combustion d’un kilogramme de pétrole libère une énergie E = 45 ´ 10 ⁶J sous forme de chaleur. Le rendement de la transformation d’énergie thermique en énergie électrique est de 34,2 %.

1 kg de pétrole 45 ´ 10 ⁶ J (calorifique)0,342 ´ 45 ´ 10 ⁶ =                       15,39 ´ 10⁶ J (électrique)

On peut donc écrire :

15,39 ´ 10 ⁶ J (électrique) nécessitent 1 kg de pétrole

1 J (électrique) nécessite 1 / ( 15,39 ´ 10 ⁶ ) kg de pétrole

4,589 ´ 10 ¹⁶ J (électrique) nécessiteraient 4,589 ´ 10 ¹⁶ / ( 15,39 ´ 10 ⁶) =           2,982 ´ 10 ⁹ kg de pétrole