Correction exercice nucléosynthèse des éléments chimiques.

Source ;http://www.chimix.com/an6/bac/fra92.htm

Question I :

1-Composition des noyaux des atomes d'hélium ⁴₂He et ³₂He ainsi que celle de l'ion hélium ⁴₂He²⁺ :

⁴₂He : 2 protons et 4-2 = 2 neutrons ;

³₂He : 2 protons et 3-2 = 1 neutron ;

⁴₂He²⁺ : 2 protons et 4-2 = 2 neutrons.

2-La synthèse des éléments chimiques plus lourds se fait par des réactions nucléaires dans lesquelles la composition du noyau est modifiée.Une réaction chimique met en jeu quelques électrons externes, sans modifier la structure du noyau.

Question II :

4 ¹₁H -->⁴₂He + 2 ⁰₁e.

1-Expression littérale de l'énergie |DE| libérée lors de cette réaction de fusion des 4 noyaux d'hydrogène.

variation de masse |Dm|= m_He +2m_e -4 m_P ;

|DE| = |Dm| c² = (m_He +2m_e -4 m_P) c² = 4 10 ^-12 J

Cas du Soleil :
Seul un dixième de sa masse M_S = 2 10³⁰ kg est constituée d'hydrogène suffisamment chaud pour être le siège de réactions de fusion soit une masse d'hydrogène égale à : m = 2 10²⁹ kg.

Or la fusion de 4 noyaux d'hydrogène, soit d'une masse de 4*1,67 10^{-27 kg d'hydrogène, libère 4 10 -12} J.

L'énergie totale E_T pouvant être produite par ces réactions de fusion est voisine de :

4 10 ^-12 *2 10²⁹ /(4*1,67 10^-27) = 2 / 1,67 10 ⁴⁴ J =1,2 10⁴⁴ J.

Des physiciens ont mesuré la quantité d'énergie reçue par la Terre et en ont déduit l'énergie E_S libérée par le Soleil en une année : 10³⁴ J.an^-1 . La durée Dt nécessaire pour que le Soleil consomme toutes ses réserves d'hydrogène est voisine de :

10⁴⁴ / 10³⁴ = 10¹⁰ ans.

Question III

⁴₂He +⁴₂He -->⁸₄Be .

On s'intéresse à la radioactivité du "béryllium 8". Soit N(t) le nombre de noyaux de "béryllium 8" présents dans l'échantillon à l'instant de date t, et N₀ celui à l'instant de date t₀ = 0 s.

La loi de décroissance radioactive s'écrit : N(t) = N₀ exp(-lt) ou encore ln (N₀ / N(t) = lt.

à t_½ , N(t_½) = ½N₀ d'où : ln2 = l T_1/2 .

Calculer le temps de demi-vie t_1/2 du "béryllium 8":T_1/2 = ln2 / l avec la constante radioactive du "béryllium 8", l = 1 10¹⁶ s^-1

T_1/2 = 0,7 / 10¹⁶ = 7 10^-17 s.

Valeur du rapport N(t₁)/N₀ à l'instant de date t₁ = 1,4 10 ^-16 s

ln (N₀ / N(t₁) = lt₁ = 10¹⁶ *1,4 10 ^-16 = 1,4 = 2*0,7 = ln2² d'où N₀ / N(t₁) = 4.

Question IV :

Expression littérale de l'énergie de liaison par nucléon E_l/A d'un noyau de fer ⁵⁶₂₆Fe , en fonction des masses du neutron m_n, du proton m_p, du noyau de "fer 56" m_Fe et de la célérité de la lumière dans le vide c.

On appelle énergie de liaison notée E_l d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos. ⁵⁶₂₆Fe compte 26 protons et 56-26 = 30 neutrons.

E_l = |m_Fe- 26m_p - 30m_n | c²

E_l/A =|m_Fe- 26m_p - 30m_n | c² / 56.

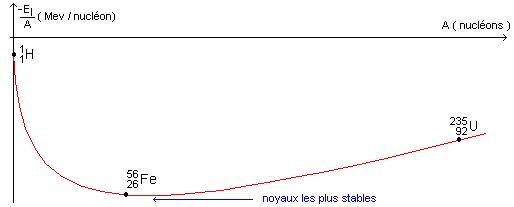
Les noyaux d'hydrogène ( et ces isotopes), d'hélium, capables de libérer de l'énergie lors d'une réaction de fusion se situent sur la partie gauche de la courbe ci-dessus.

Question V :

Lors de la désintégration radioactive du noyau de cobalt ⁵⁶₂₇Co il se forme, en plus du fer ⁵⁶₂₆Fe, une autre particule. L'équation de cette désintégration s'écrit :

⁵⁶₂₇Co --> ⁵⁶₂₆Fe* + ⁰₁e ( positrons)

suivi de la désexcitation du noyau de fer :  ⁵⁶₂₆Fe* ---> ⁵⁶₂₆Fe + ⁰₀g. ( photon )

Ce rayonnement a une énergie bien déterminée : en conséquence les niveaux d'énergie du noyau de fer sont quantifiés.

E= 1238 keV = 1,238 10⁶ eV

Exprimer cette énergie en joule : 1,238 10⁶ *1,6 10^-19 = 1,238*1,6 10^-13 J

De plus E = hn = hc/l soit l = hc/E = 6,63 10^-34 * 3 10⁸ /(1,238*1,6 10^-13)= [6,63*3/1,238] / 1,6 10^-13 =16/1,6 10^-13 = 10^{-12 m}

Ce rayonnement est un rayonnement g d'après la gamme de longueur d'onde donnée.